Après avoir effectué l’exploration des données, la sélection et, bien sûr, la mise en œuvre d’un modèle et l’obtention de résultats sous forme de probabilité ou de classe, l’étape suivante consiste à déterminer l’efficacité du modèle basé sur des métriques pour la classification.

Contenus
ToggleQuelles métriques pour la classification ?
Nous pouvons utiliser des métriques de performance de classification telles que Log-Loss, Accuracy, AUC (Area under Curve), etc. Un autre exemple de métrique pour l’évaluation des algorithmes d’apprentissage automatique est la précision, le rappel, qui peut être utilisé pour trier les algorithmes principalement utilisés par les moteurs de recherche.
Les métriques que vous choisissez pour évaluer votre modèle d’apprentissage automatique sont très importantes. Le choix des métriques influence la manière dont les performances des algorithmes d’apprentissage automatique sont mesurées et comparées. Avant de perdre plus de temps, sautons directement et voyons quelles sont ces mesures.
Matrice de confusion (confusion matrix)
La matrice de confusion est l’une des mesures les plus intuitives et les plus simples (à moins bien sûr que vous ne soyez pas confus) utilisées pour déterminer l’exactitude et la précision du modèle. Il est utilisé pour les problèmes de classification où la sortie peut être de deux types de classes ou plus.
Avant de plonger dans ce qu’est la matrice de confusion et ce qu’elle véhicule, disons que nous résolvons un problème de classification où nous prédisons si une personne a un cancer ou non.
Donnons une étiquette à notre variable cible :
1 : Lorsqu’une personne a un cancer 0 : Lorsqu’une personne n’a PAS de cancer.
Maintenant que nous avons identifié le problème, la matrice de confusion est un tableau à deux dimensions (« Actual » et « Predicted »), et des ensembles de « classes » dans les deux dimensions. Nos classifications réelles sont des colonnes et celles prévues sont des lignes.
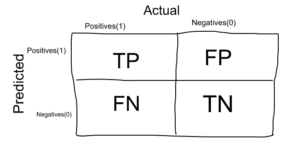
La matrice de confusion en elle-même n’est pas une mesure de performance en tant que telle, mais presque toutes les mesures de performance sont basées sur la matrice de confusion et les chiffres qu’elle contient.
Vrais positifs (TP) : les vrais positifs sont les cas où la classe réelle du point de données était 1 (vrai) et la valeur prédite est également 1.
Ex : Le cas où une personne a effectivement un cancer (1) et le modèle classant son cas comme cancer (1) relève du Vrai positif.
Vrais négatifs (TN) : les vrais négatifs sont les cas où la classe réelle du point de données était 0 (faux) et la valeur prédite est également 0.
Ex : Le cas où une personne N’A PAS de cancer et le modèle classant son cas comme Pas de cancer relève des Vrais Négatifs.
Faux positifs (FP) : les faux positifs sont les cas où la classe réelle du point de données était 0 (faux) et la valeur prédite est 1 (vrai). Faux parce que le modèle a prédit de manière incorrecte et positif parce que la classe prédite était positive.
Ex : Une personne NON atteinte de cancer et le modèle classant son cas comme un cancer relève des faux positifs.
Faux négatifs (FN) : les faux négatifs sont les cas où la classe réelle du point de données était 1 (vrai) et la valeur prédite est 0 (faux). Faux parce que le modèle a prédit de manière incorrecte et négatif parce que la classe prédite était négative.
Ex : Une personne atteinte d’un cancer et le modèle classant son cas comme sans cancer relève des faux négatifs.
Le scénario idéal que nous souhaitons tous est que le modèle donne 0 faux positif et 0 faux négatif. Mais ce n’est pas le cas dans la vraie vie car aucun modèle ne sera PAS précis à 100% la plupart du temps.
Nous savons qu’il y aura une erreur associée à chaque modèle que nous utilisons pour prédire la vraie classe de la variable cible. Cela se traduira par des faux positifs et des faux négatifs (c’est-à-dire que le modèle classe les choses de manière incorrecte par rapport à la classe réelle).
Il n’y a pas de règle stricte qui dit ce qui doit être minimisé dans toutes les situations. Cela dépend uniquement des besoins de l’entreprise et du contexte du problème que vous essayez de résoudre. Sur cette base, nous pourrions vouloir minimiser les faux positifs ou les faux négatifs.
Minimiser les faux négatifs
Disons que dans notre exemple de problème de détection du cancer, sur 100 personnes, seules 5 personnes ont un cancer. Dans ce cas, nous voulons classer correctement tous les patients cancéreux car même un modèle très MAUVAIS (Prédire tout le monde comme NON Cancéreux) nous donnera une précision de 95 % (arrivera à quelle précision).
Mais, afin de capturer tous les cas de cancer, nous pourrions finir par faire une classification lorsque la personne qui n’a PAS de cancer est classée comme cancéreuse. Cela pourrait être acceptable car il est moins dangereux que de NE PAS identifier/capturer un patient cancéreux puisque nous enverrons de toute façon les cas de cancer pour un examen plus approfondi et des rapports. Mais manquer un patient atteint de cancer sera une énorme erreur car aucun autre examen ne sera effectué sur lui.
Minimiser les faux positifs
Pour une meilleure compréhension des faux positifs, utilisons un exemple différent où le modèle classe si un e-mail est un spam ou non.
Disons que vous attendez un e-mail important, comme une réponse d’un recruteur ou une lettre d’admission d’une université. Attribuons un libellé à la variable cible et disons 1 : « L’e-mail est un spam » et 0 : « L’e-mail n’est pas un spam ».
Supposons que le modèle classe cet e-mail important que vous attendez désespérément comme spam (cas de faux positif). Maintenant, dans cette situation, c’est plutôt mauvais que de classer un spam comme important ou non spam car dans ce cas, nous pouvons toujours continuer et le supprimer manuellement et ce n’est pas pénible si cela se produit de temps en temps. Ainsi, en cas de classification des courriers indésirables, il est plus important de minimiser les faux positifs que les faux négatifs.
Exactitude (accuracy)
L’exactitude dans les problèmes de classification est le nombre de prédictions correctes faites par le modèle sur toutes sortes de prédictions faites.
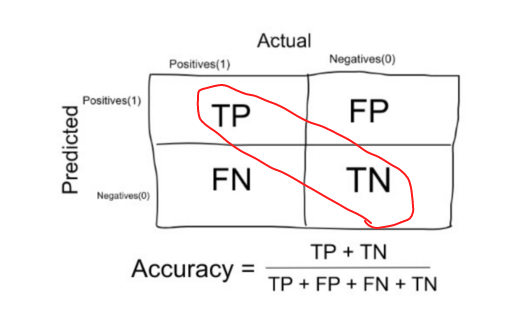
Dans le numérateur, se trouvent nos prédictions correctes (vrais positifs et vrais négatifs) (marqués en rouge dans la figure ci-dessus) et dans le dénominateur, sont le type de toutes les prédictions faites par l’algorithme (les bonnes comme les mauvaises).
L’exactitude est une bonne mesure lorsque les classes de variables cibles dans les données sont presque équilibrées.
Ex : 60 % des classes dans nos données d’images de fruits sont des pommes et 40 % sont des oranges.
Un modèle qui prédit si une nouvelle image est Apple ou Orange, 97 % des fois correctement est une très bonne mesure dans cet exemple.
L’exactitude ne doit JAMAIS être utilisée comme mesure lorsque les classes de variables cibles dans les données constituent la majorité d’une classe.
Ex : Dans notre exemple de détection du cancer avec 100 personnes, seulement 5 personnes ont un cancer. Disons que notre modèle est très mauvais et prédit que chaque cas n’est pas un cancer. Ce faisant, il a classé correctement ces 95 patients non cancéreux et 5 patients cancéreux comme non cancéreux. Maintenant, même si le modèle est terrible pour prédire le cancer, la précision d’un si mauvais modèle est également de 95 %.
Précision (precision)
Utilisons la même matrice de confusion que celle que nous avons utilisée précédemment pour notre exemple de détection du cancer.
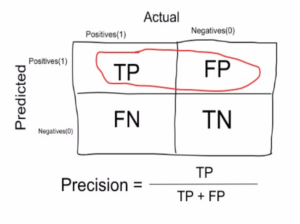
La précision est une mesure qui nous indique quelle proportion de patients chez qui nous avons diagnostiqué un cancer avait effectivement un cancer. Les positifs prédits (les personnes prédites comme cancéreuses sont TP et FP) et les personnes ayant réellement un cancer sont TP.
Ex : Dans notre exemple de cancer avec 100 personnes, seules 5 personnes ont un cancer. Disons que notre modèle est très mauvais et prédit chaque cas comme un cancer. Puisque nous prédisons que tout le monde a un cancer, notre dénominateur (vrais positifs et faux positifs) est de 100 et le numérateur, la personne atteinte d’un cancer et le modèle prédisant son cas comme un cancer est de 5. Ainsi, dans cet exemple, nous pouvons dire que la précision d’un tel modèle est de 5 %.
Rappel ou sensibilité (Recall / Sensitivity)
Le rappel est une mesure qui nous indique quelle proportion de patients ayant réellement eu un cancer a été diagnostiquée par l’algorithme comme ayant un cancer. Les vrais positifs (les personnes atteintes de cancer sont TP et FN) et les personnes diagnostiquées par le modèle ayant un cancer sont TP. (Remarque : FN est inclus parce que la personne a effectivement eu un cancer même si le modèle a prédit le contraire).

Ex : Dans notre exemple de cancer avec 100 personnes, 5 personnes ont en fait un cancer. Disons que le modèle prédit chaque cas comme un cancer.
Donc, notre dénominateur (vrais positifs et faux négatifs) est 5 et le numérateur, la personne atteinte d’un cancer et le modèle prédisant son cas comme cancer est également 5 (puisque nous avons prédit correctement 5 cas de cancer). Ainsi, dans cet exemple, nous pouvons dire que le rappel d’un tel modèle est de 100 %. Et la précision d’un tel modèle (comme nous l’avons vu ci-dessus) est de 5 %
Il est clair que le rappel nous donne des informations sur les performances d’un classificateur en ce qui concerne les faux négatifs (combien avons-nous manqué), tandis que la précision nous donne des informations sur ses performances en ce qui concerne les faux positifs (combien en avons-nous attrapés).
La précision consiste à être précis. Donc, même si nous avons réussi à capturer un seul cas de cancer, et que nous l’avons capturé correctement, nous sommes précis à 100 %.
Le rappel ne consiste pas tant à capturer correctement les cas, mais plutôt à capturer tous les cas qui ont un « cancer » avec la réponse « cancer ». Donc, si nous qualifions toujours chaque cas de « cancer », nous avons 100 % de rappel.
Donc, fondamentalement, si nous voulons nous concentrer davantage sur la minimisation des faux négatifs, nous voudrions que notre rappel soit aussi proche que possible de 100 % sans que la précision soit trop mauvaise et si nous voulons nous concentrer sur la minimisation des faux positifs, alors notre objectif devrait être de faire Précision aussi proche que possible de 100 %.
Spécificité (specificity)
La spécificité est une mesure qui nous indique quelle proportion de patients qui n’avaient PAS de cancer, ont été prédits par le modèle comme non cancéreux. Les vrais négatifs (les personnes qui n’ont PAS de cancer sont FP et TN) et les personnes que nous avons diagnostiquées comme n’ayant pas de cancer sont TN. (Remarque : FP est inclus parce que la personne n’a PAS réellement eu de cancer, même si le modèle a prédit le contraire). La spécificité est l’exact opposé du rappel.
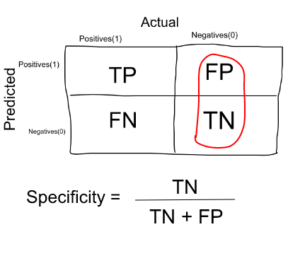
Ex : Dans notre exemple de cancer avec 100 personnes, 5 personnes ont en fait un cancer. Disons que le modèle prédit chaque cas comme un cancer.
Donc, notre dénominateur (faux positifs et vrais négatifs) est 95 et le numérateur, personne n’ayant pas de cancer et le modèle prédisant son cas comme aucun cancer est 0 (puisque nous avons prédit chaque cas comme un cancer). Donc, dans cet exemple, nous pouvons dire que la spécificité d’un tel modèle est de 0 %.
Score F1 (F1 score)
Nous ne voulons pas vraiment transporter à la fois Precision et Recall dans nos poches chaque fois que nous créons un modèle pour résoudre un problème de classification. Il est donc préférable d’obtenir un score unique qui représente à la fois la précision (P) et le rappel (R).
Une façon de le faire est simplement de prendre leur moyenne arithmétique. c’est-à-dire (P + R) / 2 où P est Précision et R est Rappel. Mais c’est assez mauvais dans certaines situations.
Supposons que nous ayons 100 transactions par carte de crédit, dont 97 sont légitimes et 3 sont des fraudes et disons que nous avons trouvé un modèle qui prédit tout comme une fraude.
La précision et le rappel de l’exemple sont illustrés dans la figure ci-dessous.
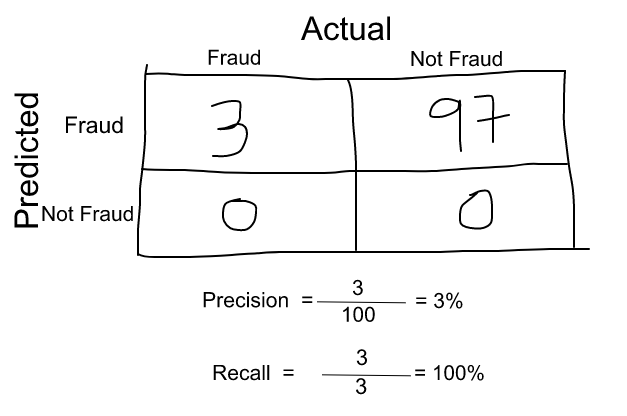
Maintenant, si nous prenons simplement la moyenne arithmétique des deux, cela donne près de 51 %. Nous ne devrions pas attribuer une note aussi modérée à un modèle terrible, car il prédit simplement chaque transaction comme une fraude.
Donc, nous avons besoin de quelque chose de plus équilibré que la moyenne arithmétique et c’est la moyenne harmonique.

La moyenne harmonique est donnée par la formule indiquée sur la figure de gauche.
La moyenne harmonique est une sorte de moyenne lorsque x et y sont égaux. Mais lorsque x et y sont différents, alors il est plus proche du plus petit nombre par rapport au plus grand nombre.
Pour notre exemple précédent, F1 Score = Harmonic Mean (Precision, Recall)
Score F1 = 2 * Précision * Rappel / (Précision + Rappel) = 2*3*100/103 = 5%
Donc, si un nombre est vraiment petit entre la précision et le rappel, le score F1 lève un drapeau et est plus proche du plus petit nombre que du plus grand, donnant au modèle un score approprié plutôt qu’une simple moyenne arithmétique.
A voir au prochain cours !
Jusqu’à présent, nous avons vu comme métriques pour la classification ce qu’est la matrice de confusion, ce qu’est l’exactitude, la précision, le rappel (ou la sensibilité), la spécificité et le score F1 pour un problème de classification. Dans le prochain article, d’autres mesures qui peuvent être utilisées comme métriques pour la classification comme la courbe AUC-ROC, la perte de journal, le score F-Beta, etc.
