Let's use the solver in Excel to find the shortest path from node S to node T in an undirected network (there will be less constraints in a directed network).
Contents
ToggleFormulate the shortest path problem with Excel
To formulate this problem of shortest way with Excel, let's answer the following three questions.
- What are the decisions to be made? For this problem, we need Excel to find out if an arc is on the shortest path or not (Yes = 1, No = 0). For example, if SB is part of the shortest path, cell F5 is equal to 1. Otherwise, cell F5 is equal to 0. (in yellow)
- What are the constraints on these decisions? The net flow (outgoing flow – incoming flow) of each node must be equal to the offer – the demand in this node. Node S should have only one outgoing arc (net flow = 1). Node T must have only one incoming arc (net flow = -1). All other nodes must have an outgoing arc and an incoming arc if the node is on the shortest path (net flow = 0) or no flow (net flow = 0). (in light blue)
- What is the overall measure of performance for these decisions? The overall measure of performance is the total distance of the shortest path, so the goal is to minimize this amount. (in dark blue)
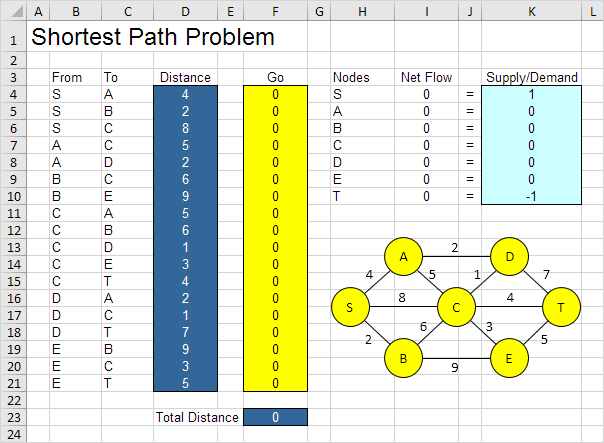
Let's name the following ranges:
| Beach name | Cells |
|---|---|
| From | B4: B21 |
| To | C4: C21 |
| Distance | D4: D21 |
| Go | F4: F21 |
| NetFlow | I4: I10 |
| SupplyDemand | K4: K10 |
| TotalDistance | F23 |
And let's insert the following functions:
Solve the model
Let’s enter the solver parameters:
The optimal solution is:







