Contenus
ToggleProgrammation logique par contraintes
Cette page présente des exercices corrigés détaillés du problème de programmation logique par contraintes, qui est un mélange naturel de la programmation logique et la programmation par contraintes.

Exercice 1
On considère le puzzle suivant :
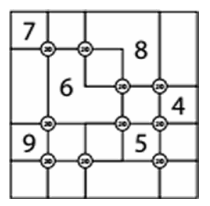
Chaque région de la grille doit être remplie par un nombre entre 0 et 9 de sorte que
- les nombres dans deux régions adjacentes (verticalement ou horizontalement) soient différents
- à chaque fois qu’il y a quatre régions qui se rencontrent en un point (indiqué par un petit rond), la somme de leurs nombres soient égale à 20.
Résoudre ce problème par programmation logique par contraintes.
Nommons de haut à gauche vers le bas à droite (par ligne) les cases vides par une lettre. Chaque domaine a une valeur comprise entre 0 et 9. Par la suite, il faut remplir les deux contraintes à la main.
Pour chaque case, son score doit être différent de ses voisines.
Pour chaque rond, la somme doit être égale à 20.
Nous avons donc la programmation logique par contraintes suivante :
L = [A,B,C,D,E,F,G,H,I,J,K,M],
L :: [0..9],
A #\= 7, A #\= 8, A #\= 6,
B #\= 8, B #\= 4,
C #\= 7, C #\= 6, C #\= 9,
D #\= 6, D #\= 8,
E #\= 6, E #\= 8, E #\= 4, E #\= 5,
F #\= 9, F #\= 6, F #\= G, F #\= J,
G #\= 6, G #\= 5, G #\= K,
H #\= 5, H #\= 4, H #\= M,
I #\= 9, I #\= J, J #\= K,
K #\= 5, K #\= M,
7+6+A+C #= 20, A+6+8+D #= 20, 6+8+D+E #= 20, 4+8+B+E #= 20,
9+6+C+F #= 20, 5+6+E+G #= 20, 4+5+E+H #= 20,
9+F+I+J #= 20, F+G+J+K #= 20, 5+H+K+M #= 20,
labeling(L).
Exercice 2
On considère le jeu Bokkusu. Le but du jeu est de marquer en noir certaines cases de la grille donnée.
Chaque case a deux valeurs : une valeur A et une valeur B. Les nombres à droite dénotent les valeurs A des cases de chaque ligne correspondante et les nombres en bas déenotent les valeurs B des cases de chaque colonne correspondante (Ces valeurs vont toujours de 1 à la taille de la grille en augmentant de 1 de gauche à droite ou du haut vers le bas).
Les valeurs à gauche indiquent la somme des valeurs B des cases noires pour chaque ligne et les valeurs en haut indiquent la somme des valeurs A des cases noires pour chaque colonne. Un exemple d’une grille et sa solution est donné dans la figure. Dans la solution de cette exemple on a par exemple 7 = 1 + 2 + 4 (les cases avec valeur B de 1, 2 et 4 sont marquées noir) et 6 = 2 + 4 (les cases avec valeurs A de 2 et 4 sont marquées).

Résoudre ce problème par programmation logique par contraintes.
Nommons chaque case de la grille de façon matriciel. Pour les contraintes, il faut que la somme des variables binaires (blanc=0 ou noir=1) multiplié par les coefficients à gauche ou en haut soient égale à la valeur en face.
L = [X11,X12,X13,X14,
X21,X22,X23,X24,
X31,X32,X33,X34,
X41,X42,X43,X44],
fd_domain(L,0,1),
X11 + 2*X12 + 3*X13 + 4*X14 #= 3,
X21 + 2*X22 + 3*X23 + 4*X24 #= 7,
X31 + 2*X32 + 3*X33 + 4*X34 #= 1,
X41 + 2*X42 + 3*X43 + 4*X44 #= 2,
X11 + 2*X21 + 3*X31 + 4*X41 #= 5,
X12 + 2*X22 + 3*X32 + 4*X42 #= 6,
X13 + 2*X23 + 3*X33 + 4*X43 #= 1,
X14 + 2*X24 + 3*X34 + 4*X44 #=2
Exercice 3
On considère le problème de générer un emploi de temps. Il y a 7 cours et 4 créneaux. Un créneaux peut accueillir au maximum 2 cours. Il y a les contraintes suivantes :
– Cours 4 doit être avant cours 6.
– Cours 5 doit être avant cours 7.
– Cours 6 doit être avant cours 2.
– Cours 1 ne peut pas être en parallèle avec les cours 2, 3, 4 et 7.
– Cours 2 ne peut pas être en parallèle avec les cours 3 et 6.
– Cours 3 ne peut pas être en parallèle avec les cours 4, 5 et 6.
– Cours 4 ne peut pas être en parallèle avec les cours 5 et 6.
– Cours 5 ne peut pas être en parallèle avec le cours 7.
Résoudre ce problème par programmation logique par contraintes.
On va considérer que les cours sont des domaines, et qu’ils peuvent prendre une valeur de 1 à 4 correspondant au créneau qui sera choisi. La programmation logique par contraintes est la suivante :
L = [C1,C2,C3,C4,C5,C6,C7],
fd_domain(L,1,4),
C4 #< C6, C5 #< C7, C6 #< C2,
C1 #\= C2, C1 #\= C3, C1 #\= C4, C1 #\= C7,
C2 #\= C3, C2 #\= C6,
C3 #\= C4, C3 #\= C5, C3 #\= C6,
C4 #\= C5, C4 #\= C6,
C5 #\= C7,
fd_cardinality(1,[C1#=1,C2#=1,C3#=1,C4#=1,C5#=1,C6#=1,C7#=1],2),
fd_cardinality(1,[C1#=2,C2#=2,C3#=2,C4#=2,C5#=2,C6#=2,C7#=2],2),
fd_cardinality(1,[C1#=3,C2#=3,C3#=3,C4#=3,C5#=3,C6#=3,C7#=3],2),
fd_cardinality(1,[C1#=4,C2#=4,C3#=4,C4#=4,C5#=4,C6#=4,C7#=4],2),
fd_labeling(L)
Exercice 4
Inshi no heya est un jeu logique japonais. Il est joué sur une grille rectangulaire de cellules qui est séparée en rectangles. Une dimension de chaque rectangle est 1 tandis que l’autre dimension varie.
Chaque rectangle est placé horizontalement ou verticalement et contient un nombre. Le but est de
remplir toutes les cellules avec des chiffres de 1 à 9 de sorte que :
– Si on multiplie tous les chiffres de chaque rectangle on obtient le nombre indiqué dans le rectangle
– Aucun chiffre apparait plusieurs fois dans une colonne.
– Aucun chiffre apparait plusieurs fois dans une ligne.
Un exemple d’une grille d’origine et une solution sont donné ci-dessous :

Résoudre ce problème par programmation logique par contraintes.
Chaque case de la matrice est considéré comme un domaine, chaque case peut prendre une valeur de 1 à 5. Les contraintes sont simples puisque la somme des cases d’un certain périmètre doit être égale à un nombre donné.
L = [X11,X21,X31,X41,X51,
X12,X22,X32,X42,X52,
X13,X23,X33,X43,X53,
X14,X24,X34,X44,X54,
X15,X25,X35,X45,X55],
fd_domain(L,1,9),
fd_all_different([X11,X12,X13,X14,X15]),
fd_all_different([X21,X22,X23,X24,X25]),
fd_all_different([X31,X32,X33,X34,X35]),
fd_all_different([X41,X42,X43,X44,X45]),
fd_all_different([X51,X52,X53,X54,X55]),
fd_all_different([X11,X21,X31,X41,X51]),
fd_all_different([X12,X22,X32,X42,X52]),
fd_all_different([X13,X23,X33,X43,X53]),
fd_all_different([X14,X24,X34,X44,X54]),
fd_all_different([X15,X25,X35,X45,X55]),
X11 #= 5, X31*X41 #= 2, X32*X42 #= 4, X33 #= 4,
X43*X53 #= 15, X34*X44 #= 15, X15*X25*X35*X45 #= 120,
X21*X22 #= 15, X51*X52 #= 12, X12*X13*X14 #= 8,
X23*X24 #= 2, X54*X55 #= 2,
fd_labeling(L)
Exercice 5
Des gratte-ciel sont construits sur une grille NxN. Chaque gratte-ciel a un nombre d’étages correspondant à sa taille (de 1 à N). Dans chaque colonne et chaque ligne chaque taille apparait exactement une fois. Les nombres sur les bords de la grille indiquent combien de gratte-ciel peuvent être vus en regardant de ce point vers la ligne ou la colonne correspondante. Un gratte-ciel est visible, si tous les gratte-ciel devant lui sont plus petits. Voici l’exemple d’une grille et de sa solution :
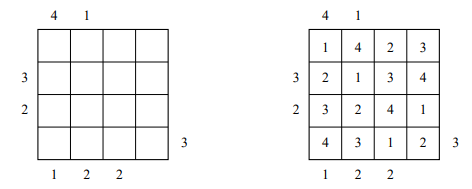
Par exemple, dans la deuxième ligne du bas en regardant de la gauche on peut voir 2 gratte-ciel : celui d’hauteur 3 et celui d’hauteur 4. Voici un deuxième problème d’une grille (5×5) à résoudre :

Résoudre ce problème par programmation logique par contraintes.
Vous pouvez utiliser le prédicat prédéfini fd_cardinality(+List, ?Count)
où List est une liste de contraintes et Count le nombre de contraintes de List satisfaites.
contrainte([A1,A2,A3,A4,A5],C) :-
fd_cardinality([A5 #> A4 #/\ A5 #> A3 #/\ A5 #> A2 #/\ A5 #> A1,
A4 #> A3 #/\ A4 #> A2 #/\ A4 #> A1,
A3 #> A2 #/\ A3 #> A1, A2 #> A1],C).
gratteciel(L) :-
L = [Line1,Line2,Line3,Line4,Line5],
Line1 = [X11,X12,X13,X14,X15],
Line2 = [X21,X22,X23,X24,X25],
Line3 = [X31,X32,X33,X34,X35],
Line4 = [X41,X42,X43,X44,X45],
Line5 = [X51,X52,X53,X54,X55],
fd_domain(Line1,1,5),fd_domain(Line2,1,5),
fd_domain(Line3,1,5),fd_domain(Line4,1,5),
fd_domain(Line5,1,5),
fd_all_different(Line1),fd_all_different(Line2),
fd_all_different(Line3),fd_all_different(Line4),
fd_all_different(Line5),
fd_all_different([X11,X21,X31,X41,X51]),
fd_all_different([X12,X22,X32,X42,X52]),
fd_all_different([X13,X23,X33,X43,X53]),
fd_all_different([X14,X24,X34,X44,X54]),
fd_all_different([X15,X25,X35,X45,X55]),
% Le premier gratte-ciel est toujours visible. Il faut donc enlever 1
% de chaque nombre de gratte-ciel visible.
contrainte(Line1,0), contrainte(Line2,3), contrainte(Line3,2),
contrainte(Line4,1),
contrainte([X12,X22,X32,X42,X52],2),
contrainte([X13,X23,X33,X43,X53],2),
contrainte([X15,X14,X13,X12,X11],2),
contrainte([X25,X24,X23,X22,X21],1),
contrainte([X35,X34,X33,X32,X31],2),
contrainte([X55,X54,X53,X52,X51],0),
contrainte([X52,X42,X32,X22,X12],1),
contrainte([X53,X43,X33,X23,X13],1),
contrainte([X54,X44,X34,X24,X14],1),
contrainte([X55,X45,X35,X25,X15],0),
fd_labeling(Line1),fd_labeling(Line2),fd_labeling(Line3),
fd_labeling(Line4),fd_labeling(Line5).
