Erreurs de forecasting

Contenus

Voici les principales mesures pour mesurer les erreurs de forecasting :

Mesure dépendant de l’échelle :

MAE, MDAE, MSE, RMSE

En pourcentage :

MAPE, sMAPE, MASE, sMdAPE

En relatif :

MRAE, MdRAE, RelMAE
U-statistic

Mesures dépendants de l'échelle

Nous utilisons la terminologie suivante : si y1, …, yn représente une série temporelle, alors ŷi représente la ième valeur prévue, où i ≤ n. Pour i ≤ n, la ième erreur ei (alias résiduel) est alors

Notre objectif est de trouver une prévision qui minimise les erreurs. Un certain nombre de mesures sont couramment utilisées pour déterminer l’exactitude d’une prévision. Il s’agit notamment de l’erreur absolue moyenne (MAE), de l’erreur quadratique moyenne (MSE) et de l’erreur quadratique moyenne (RMSE).

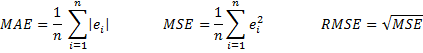
MdAE calcule la différence absolue médiane entre deux vecteurs numériques.

réel <- c(1,1, 1,9, 3,0, 4,4, 5,0, 5,6)
prédit <- c(0,9, 1,8, 2,5, 4,5, 5,0, 6,2)
mdae (réel, prévu)

Mesures en pourcentage

Certaines autres mesures sont l’erreur de pourcentage absolue moyenne (MAPE), l’erreur d’échelle absolue moyenne (MASE) et l’erreur de pourcentage absolue moyenne symétrique (SMAPE).

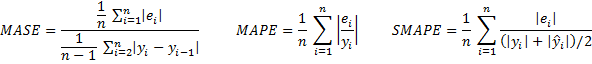
Erreur d’échelle absolue médiane (MdASE). Prendre la médiane au lieu de la moyenne des erreurs absolues de test et d’entraînement rend cette métrique plus robuste aux valeurs aberrantes puisque la médiane a tendance à être une mesure plus robuste de la tendance centrale en présence de valeurs aberrantes.

Comme MASE et d’autres mesures de performances à l’échelle, cette mesure sans échelle peut être utilisée pour comparer les méthodes de prévision sur une seule série ou entre des séries.

Tout comme MASE, cette métrique est bien adaptée aux séries à demande intermittente car elle ne donnera pas de valeurs infinies ou indéfinies à moins que les données d’entraînement ne soient une série temporelle plate. Dans ce cas, la fonction renvoie une grande valeur au lieu de inf.

Theil U Statistique

Enfin, il y a la statistique U de Theil, qui est calculée par la formule

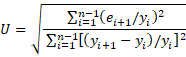
Si U < 1, la technique de prévision est meilleure que la supposition. Si U = 1, alors la technique de prévision équivaut à une estimation. Si U > 1, alors la technique de prévision est pire que la supposition.

En fait, U est également appelé statistique U2 de Theil. Il existe également une statistique U1 moins souvent utilisée

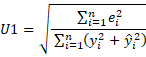
U1 prend des valeurs comprises entre 0 et 1, les valeurs plus proches de 0 représentant une plus grande précision des prévisions.

Mesures relatives

Et voici les mesures en relatif :

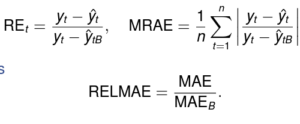
Ici la prédiction est à comparer à la prédiction B dite de référence.