Contenus
ToggleFiles d’attente
Une file d’attente (ou des files d’attente) peut être décrit ainsi : des clients (hommes, taches, messages, etc.) arrivent pour un service, attendent dans une file s’ils ne peuvent pas être pris en charge immédiatement, et repartent après avoir eu le service.
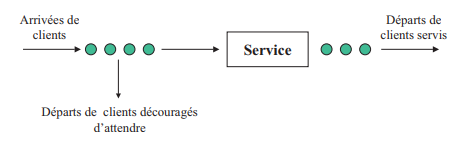
Le modèle, originalement créé par Erlang pour le système téléphonique de 1909, permet de modéliser la gestion de trafic, la planification et le dimensionnement d’infrastructures et d’usinage.
Notation de Kendall
Une file d’attente possède 6 critères notées par : T/X/C/K/P/Z
- T : la distribution de probabilité du temps inter-arrivées. Les clients peuvent partir s’ils arrivent alors que la file est pleine. T pourra prendre les valeurs suivantes
- M pour processus markovien / loi exponentielle
- G pour la loi générale
- D loi déterministe
- E(k) pour le loi d’Erlang
- etc.
- X : la distribution de probabilité du temps de service. Un client est pris directement par un serveur libre, une fois le service accompli le client part. La distribution est représentée par les même symboles que dans T.
- C : le nombre de serveurs. Dans les files d’attentes simples, les serveurs ont tous la même distribution de probabilité de temps de service.

- K : la capacité de la file. Si la file est un nombre finie, le client est perdu lorsque la file est pleine. Les serveurs comptent dans la capacité de la file (1 par serveur).
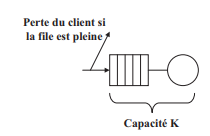
- P : la taille de la population. La taille de la population est finie ou infinie. Dans le cas d’une population finie, le taux d’arrivée des clients est fonction du nombre de client dans le système.
- Z : la discipline de service
- FCFS/FIFO (first come first served / first in first out): premier arrivé premier servi
- LCFC/FILO (last come first served / first in last out): dernier arrivé premier servi / premier arrivé dernier servi
- RANDOM : service du client aléatoire dans la liste d’attente
- HL (hold in line) : si un client « important » arrive, il prend la première place dans la file d’attente (en fonction de l' »importance » des premiers clients)
- PR (preemption) : si un client « important » arrive, il est servi directement et le client « moins important » quitte le service pour aller dans la file
- PS (processor sharing) : tous les clients sont servis en même temps avec une vitesse inversement proportionnelle au nombre de clients
- etc.
Une file d’attente peut être parcourue par différentes classes de clients caractérisées par :
- Des processus d’arrivée différents
- Des temps de service différents
- Des coûts différents
- Un ordonnancement dans la file d’attente en fonction de leur classe
On utilisera la notation T/X/C quand la file est de capacité infinie, la taille de la population est infinie et que le service est de discipline FIFO. Cela revient à écrire T/X/C/∞/∞/FIFO.
Mesures de performance
L’étude d’une file d’attente a pour but de calculer ou d’estimer les performances d’un systèmes. Ce calcul se fait en régime stationnaire afin de calculer : le débit X, le nombre de clients Q, le taux d’utilisation du serveur U, le temps de réponse R. En général, on calcule les espérances de ces paramètres.
Dans le cadre des files simples, le système est ergodique. On cherche alors à calculer la stabilité du système. Prenons les éléments suivant :
- A(T) : nombre d ’arrivées dans le système entre 0 et T
- D(T) : nombre de départs du système entre 0 et T
- Xe(T) = A(T)/T : débit moyen d’entrée entre 0 et T
- Xs(T) = D(T)/T : débit moyen de sortie entre 0 et T
- Q(T) : nombre de clients moyen entre 0 et T
- Rk: temps de séjour du kième client arrivé
 : temps moyen de séjour entre 0 et T
: temps moyen de séjour entre 0 et T
une file d’attente est stable si et seulement si la limite quand T tend vers l’infini du débit moyen d’entrée est égale à la limite quand T tend vers l’infini du débit moyen de sortie. Autrement dit, quand la limite quand T tend vers l’infini de D(T)/A(T)=1. Dans une file stable, le nombre de clients reste fini.
Soit Q le nombre moyen de clients, R le temps moyen de réponse et X le débit moyen, la loi de Little garanti en régime permanent pour un système stable que Q=RX (on ne tient alors plus compte de T).

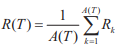 : temps moyen de séjour entre 0 et T
: temps moyen de séjour entre 0 et T