Ecarts complémentaires

Écarts complémentaires

Les écarts complémentaires sont utilisable si le primal est réalisable et que la solution est bornée, le dual est réalisable et sa solution est aussi borné. Si les valeurs des solutions primale et duale sont égales, elles sont optimales pour leur programme linéaire, on parle de dualité forte. Parfois il n’est pas possible de trouver de solution, ou pas utile de la calculer. Le programme primal et dual étant lié, il est possible de déduire une solution du programme réciproque à l’aide des écarts complémentaires.

Processus

L’un des principaux théorèmes de la théorie de la dualité en programmation linéaire est le théorème des écarts complémentaires. Ce théorème nous permet de trouver la solution optimale du problème dual lorsque nous connaissons la solution optimale du problème primal (et inversement) en résolvant un système d’équations formées par les variables de décision (primal et dual) et les contraintes (primal et dual modèle).

L’importance de ce théorème est qu’il facilite la résolution des modèles d’optimisation linéaire, ce qui vous permet de trouver le modèle le plus simple à traiter (du point de vue algorithmique). Le processus est le suivant:

1. Trouver une solution réalisable sur le primal.
2. Si tel est le cas, notez les variables non nulles (cela implique que la contrainte du dual est saturé) et les contraintes avec du jeu (ce qui implique que la variable du dual est nulle).
3. Résoudre le système d’équations
4. Vérifier la dualité forte, c’est à dire que la solution du primal est identique à celle du dual. Dans ce cas la solution réalisable est un optimum.

Version I. Soient x* et y* les solutions du primal et du dual. Ces deux solutions sont optimales si et seulement si :

• pour tout j de 1 à n
  • soit la contrainte j du dual est saturée
  • soit x*_j=0
  • ou les deux
• pour tout i de 1 à m
  • soit la contrainte i du primal est saturée
  • soit y*_i=0
  • ou les deux

La deuxième version des écarts complémentaires permettent de mieux comprendre comment trouver une solution dans le programme réciproque. Pour cela il faut supposer que les deux conditions de la version I soit toujours vrai.

Version II. Une solution x du primal est optimale si et seulement si il existe un vecteur y* tel que :

• y* est admissible
• si x_j>0 alors la j-ème contrainte du dual est saturée
• si la i-ème contrainte du primal n’est pas saturée alors y*_i=0.
• et inversement entre le dual et le primal.

Ainsi, une fois une solution trouver dans le programme réciproque, il ne reste plus qu’à vérifier la dualité forte du système.

Exemple 1

Considérons le modèle de programmation linéaire suivant avec 2 variables dont la solution optimale est X = 14/5 et Y = 8/5 avec la valeur optimale V = 20,8.

Le modèle dual associé au modèle primal est:

Ensuite, le théorème des écarts complémentaires montre les relations suivantes:

Comme nous le savons, X = 14/5 et Y = 8/5 (solution optimale primale). Si nous remplaçons ces valeurs de X et Y dans les troisième et quatrième équations (car les deux contraintes du primal sont saturés et nous ne pouvons rien conclure sur les équations 1 et 2), nous générons un système d’équations en termes de A et de B dont la solution correspond à A = 6/5 et B = 2/5. Si nous évaluons ensuite la fonction objectif dans le problème dual de cette solution, nous obtenons: V = 12 (6/5) +16 (2/5) = 20,8, ce qui est similaire à la valeur optimale du problème primal (dualité forte).

Exemple 2

Prenons le problème suivant :

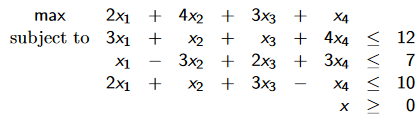
La solution à ce problème est {42, 0, 10.4, 0, 0.4}. Le problème dual est le suivant:

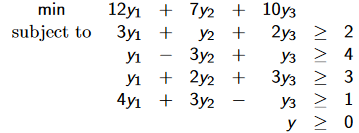
Test de faisabilité. La première contrainte est saturé, aucune conclusion pour y1. La deuxième contrainte n’est pas saturé, donc y2 = 0. La troisième contrainte est saturé, rien sur y3.

Variables positives. x1 = 0, rien à conclure. x2> 0, la deuxième contrainte du dual est saturée. x3 = 0, rien à conclure. x4> 0, quatrième contrainte du dual est saturée.

Donc, la solution à dual doit satisfaire: y2 = 0; y1 + y3 = 4; 4y1 + y3 = 1 avec {1, 0, 3} comme solution. Les valeurs du primal et dual sont équivalentes donc on a l’optimum.