Algorithme A étoile

Contenus

L’idée de l’algorithme A étoile ou A star ou A*, est d’éviter de développer des chemins estimés trop cher par rapport à ceux connus. Pour cela l’algorithme fera référence à une fonction d’évaluation de son coût total. Le principe est similaire a du branch&bound ou branch&price.

Fonction d’évaluation

Soient f(n) une fonction d’évaluation pour un sommet n, h(n) une heuristique de coût estimé pour aller vers un état final, et g(n) le coût réel pour atteindre le sommet n. Alors f(n) = h(n)+g(n). La fonction f(n) peut se décrire comme le coût total estimé pour aller vers un état final en passant par n.

L’heuristique doit être admissible, c’est-à-dire que h(n)≤h'(n) où h'(n) est le vrai coût pour aller de n vers un état final. L’heuristique ne sur-estime jamais la vraie distance. Et elle est consistante, c’est-à-dire que pour tout y descendant de x, h(x)≤h(y)+cout(x à y).

Algorithme A étoile

Notons s l’état initial, T l’ensemble des états terminaux, k(x,y) le coût de x à y, F l’ensemble des états développés – dont les successeurs ont été générés (ensemble des fermés) – et O l’ensemble des états générés mais non développés. L’algorithme A étoile est le suivant :

O Tant que O <> Ø faire
    Extraire de O l'élément x tq f(x) est minimale;
    Insérer x dans F;
    Si x appartient à T alors Fini : Solution trouvée
    Sinon
      Pour tout y successeur de x faire
        Si y n'appartient pas à F U O ou g(y) > g(x) + k(x,y) alors
          g(y) Fin Si
      Fin Pour
    Fin Si
  Fin Tant Que /CODE+

Exemple

Pour illustrer l’algorithme A étoile, nNous prendrons pour exemple le problème du 8-puzzle. Ce problème est une matrice de 3*3 contenant 8 cases remplies par les chiffres de 1 à 8 et une case vide. Chaque case peut se déplacer sur une case adjacente dans la matrice, et uniquement sur une case vide. Dans ce cas, nous permettons la valeur de la case avec la case vide. L’objectif du 8-puzzle est de trier les cases par ordre croissant de gauche à droite et de haut en bas de la matrice. Concrètement, il s’agit d’un taquin.

L’heuristique utilisée pour cet exemple est la Distance de Manhattan. Cette distance est la somme des mouvements « à vol d’oiseau » à effectuer pour que chaque case soit à la bonne place. Il s’agit bien d’une heuristique admissible et consistante car nous considérons que tous les mouvements des cases sont légaux. La fonction g(n) aura pour valeur n, le nombre de déplacement effectué pour atteindre la configuration n.

Prenons une configuration aléatoire de départ, nous avons pour première itération l’arbre suivant :

plus court chemin algorithme A étoile algorithme A*

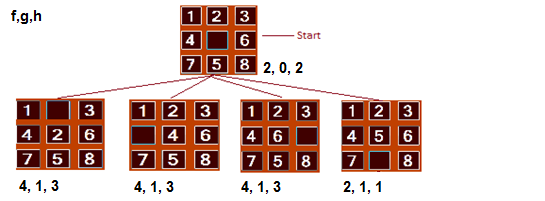
L’algorithme a dans l’ensemble F la racine, et dans l’ensemble O les 4 configurations générées. La configuration de droite possède la plus petite estimation du coût total, elle est donc retirée de O pour être explorée et finalement être placée dans F. Nous obtenons l’arbre suivant :

Nous avons trouvé une solution finale telle que son coût soit minimal, l’algorithme A étoile s’arrête.