Contenus
ToggleAlgorithme de Johnson
L’algorithme de Johnson calcule les plus courts chemins pour tout couple de sommets du graphe. Il a une bonne complexité pour les graphes creux (peu d’arêtes en comparaison du nombre de sommets).
Il utilise les algorithmes de Dijkstra et de Bellman-Ford, et renvoie soit la matrice des poids des plus courts chemins, soit l’assertion que le graphe possède un circuit de poids négatif.
La technique utilisée consiste à se ramener au cas avec uniquement des poids positifs, puis de faire tourner l’algorithme de Dijkstra en partant de chaque sommet. Si les poids ne sont pas tous positifs, on les redéfinit pour pouvoir se ramener au premier cas.
L’algorithme de Johnson est composé des étapes suivantes :
- Ajouter un nouveau nœud q au graphe, et connecter ce nœud par des arcs de poids nul à tous les autres nœuds.
- Utiliser l’algorithme de Bellman-Ford en partant du nouveau nœud q pour déterminer, pour chaque sommet v, le poids minimum h(v) d’un chemin de q à v. Si on détecte un cycle négatif, l’algorithme s’arrête sur un échec.
- Repondérer les arcs du graphe initial en utilisant les valeurs calculées par l’algorithme de Bellman-Ford : un arc de u à v, dont l’ancien poids ou longueur est le nombre w(u,v), a pour nouvelle longueur le nombre non négatif w(u,v) + h(u) − h(v).
- Enlever le sommet q et utiliser l’algorithme de Dijkstra pour déterminer les chemins les plus courts.
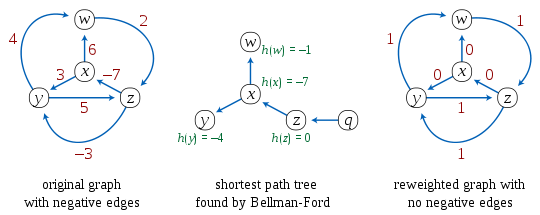
Exemple de l’algorithme de Johnson :