Arbres et arborescences - Complex systems and AI

Contenus

Arbres et arboresences

Les arbres et arborescences sont des graphes particuliers souvent utilisés pour représenter l’aide à la décision, des données, ou pour le calcul de la complexité.

Un arbre est un ensemble organisé de nœuds dans lequel chaque nœud a un père et un seul, sauf un nœud que l’on appelle racine. Si un nœud p est le père du nœud f, alors f est un fils de p; si f n’a pas de fils, alors c’est une feuille. Il est possible de stocker tout type d’information dans les nœuds ou les liens.

Terminologie

Un nœud est défini par son étiquette et ses sous-arbres. Il est donc possible de représenter un arbre par un n-uplet <e,a₁,…,a_k> dans lequel e est l’étiquette du nœud et a_i sont ses sous-arbres.

Par exemple, les calculateurs organisent les expressions mathématiques en fonction de la priorité des opérateurs et de leur profondeur : (y/2 – x)*(75+z) sera représenté par <*,<-,,>,>,<+,,>>. L’opération se fait alors par un parcours particulier de l’arbre :

les descendants d’un nœud sont les nœuds de ses sous-arbres;
un ancêtre d’un nœud est soit son père, soit un ancêtre de son père;
le chemin d’un nœud à la racine est constitué de tous ses ancêtres;
le frère d’un nœud est un fils de son père autre que lui-même.

Un arbre est souvent représenté par un graphe pour faciliter la lecture :

Les nœuds d’un arbre se répartissent par profondeurs (ou niveaux). La profondeur 0 contient uniquement la racine, la profondeur 1 ses fils etc. La hauteur d’un arbre est le nombre de profondeurs, ou la taille du plus grand chemin d’un nœud à la racine.

Définition : théorie des graphes

Étant donné un graphe non orienté comportant n sommets, les propriétés suivantes sont équivalentes :

Le graphe est connexe et sans cycle,
Le graphe est sans cycle et possède n-1 arêtes,
Le graphe est connexe et admet n-1 arêtes,
Le graphe est sans cycle, et en ajoutant une arête, alors on crée un et un seul cycle élémentaire,
Le graphe est connexe, et en supprimant une arête quelconque il n’est plus connexe,
Il existe une chaîne et une seule entre toutes paires de sommets.

Une arborescence est un graphe orienté sans circuit admettant une racine telle que pour tout autre sommet il existe un chemin unique de la racine vers ce sommet. Une arborescence possède des propriétés similaires à l’arbre.

Arbre binaire

Dans un arbre binaire, chaque nœud a un fils gauche et un fils droit, qui peuvent être des sous-arbres nuls. Un arbre binaire est complet si toutes ses feuilles ont la même profondeur et que tous ses nœuds qui ne sont pas des feuilles ont deux fils.

Déterminons le nombre total de feuilles et de nœuds d’un arbre binaire complet.

À la profondeur 0, il y a une feuille, la racine. Supposons que l’arbre binaire complet possède 2^(h-1) feuilles à la hauteur h. Alors, à la hauteur h+1, chacune de ces feuilles devient un nœud avec deux fils, on a donc un nombre de feuilles de 2*2^(h-1) = 2^h. CQFD.

De plus, le nombre de nœuds du graphe binaire complet est égal à la somme du nombre de feuille des arbres binaires complets de hauteur inférieure. On en déduit que le nombre total de nœud est ∑_(i=0)^(h-1) 2ⁱ = 2^h -1. Réciproquement, si un graphe binaire complet possède n nœuds, alors sa hauteur est d’après la formule précédente log₂ (n)+1. On en déduit qu’un arbre binaire quelconque est au moins de hauteur log₂ (n) +1.

Un arbre binaire équilibré ou arbre AVL est un arbre binaire tel que les hauteurs des deux sous-arbres de tout noeud de l’arbre diffèrent de 1 au plus. Un sous-arbre d’un arbre AVL est aussi un arbre AVL.

L’indicateur sur les sommets indique la différence entre la hauteur du sous-arbre gauche et la hauteur du sous-arbre droit.

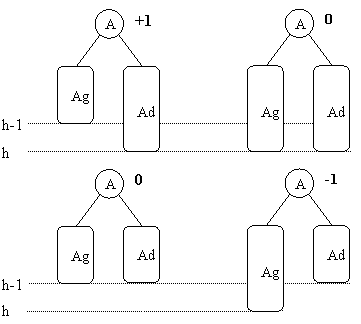
Lorsque l’arbre est déséquilibré, il faut alors permuter les sommets parents et la racine tout en conservant l’ordre des sous-arbres (voir la suite sur les arbres de recherche).

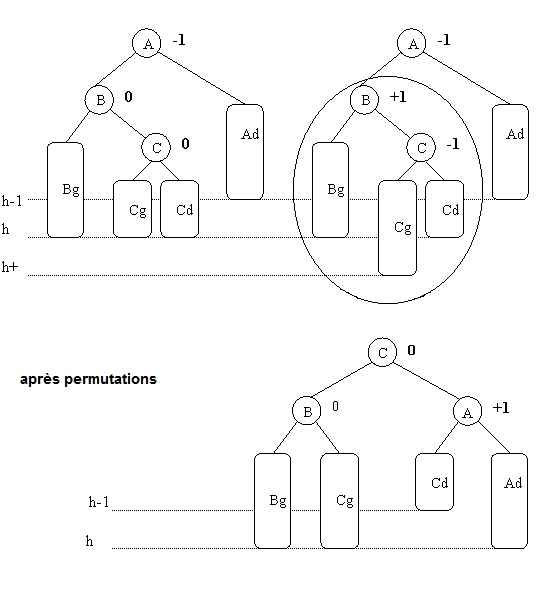
Nous pouvons agrandir la définition sur les arbres de degré supérieur (arbre ternaire etc). Seul le coefficient 2 est modifié en fonction du nombre de fils définis par le type d’arbre.

Arbre de recherche

Un arbre de recherche est une structure de données permettant de représenter un ensemble de valeurs si l’on dispose d’une relation d’ordre sur ces dernières. Les opérations standards sur les arbres de recherche sont : l’insertion, la suppression ou la recherche d’une valeur. Ces opérations sont peu coûteuses si l’arbre est équilibré. Afin de faciliter la compréhension, nous travaillerons sur des arbres binaires de recherche (ABR).

Soient un ensemble de valeurs E muni d’une relation d’ordre, et soit A un arbre binaire. L’arbre A est un ABR de E si pour tout nœud p de A, la valeur de p est strictement plus grande que les valeurs de son sous-arbre gauche, et est strictement plus petite que les valeurs figurant dans son sous-arbre droit; à condition que les valeurs soient uniques. Les valeurs sont appelées clés.

La valeur la plus petite est le dernier descendant gauche de la racine, et la plus grande est le dernier descendant droit de la racine. D’autres critères logiques peuvent être déduits de la définition :

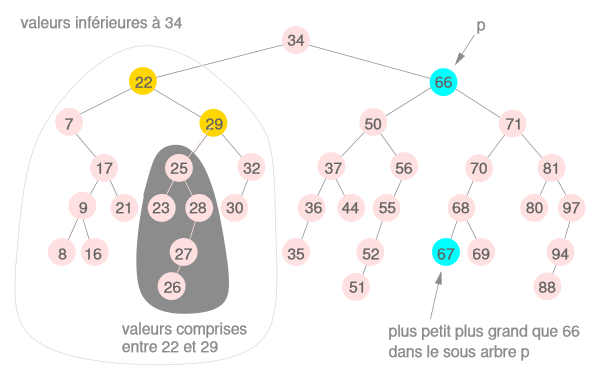
Les trois actions se font alors grâce à des parcours de l’ABR.