Livre #1
Livre #1
Contenus
ToggleParcours d’arbre
Pour parcourir un graphe, nous construisons d’abord un arbre couvrant de ce dernier. On parlera alors de parcours d’arbre.
Parcours en largeur
Dans le parcours en largeur, on parcourt par profondeur croissante à la racine.

ParcoursLargeur(Graphe G, Sommet s):
{
f = CreerFile();
f.enfiler(s);
marquer(s);
tant que non f.vide()
s = f.defiler();
afficher(s);
pour tout voisin t de s dans G
si t non marqué FAIRE
f.enfiler(t);
marquer(t);
fin si
fin pour
fin tant que
}Parcours en profondeur : préfixe
Les parcours en profondeur sont des parcours récursifs. Dans le parcours préfixe, nous parcourons toujours le sous-arbre gauche avant de traiter le sous-arbre droit.
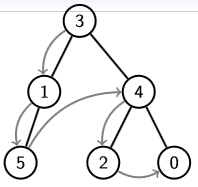
ParcoursPrefixe(Graphe G):
{
si (G==NULL) return;
afficher(racine);
ParcoursPrefixe(a.gauche);
ParcoursPrefixe(a.droite);
}Parcours en profondeur : infixe
Le parcours en profondeur en infixe consiste à aller le plus à gauche possible, et d’afficher les branches de gauche à droite. Cela revient à afficher les diagonales / de bas en haut.
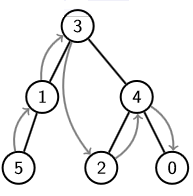
ParcoursInfixe(Graphe G):
{
si (G==NULL) return;
ParcoursPrefixe(a.gauche);
afficher(racine);
ParcoursPrefixe(a.droite);
}Parcours en profondeur : postfixe
Il s’agit d’un parcours des diagonales \ de haut en bas.

ParcoursPostfixe(Graphe G):
{
si (G==NULL) return;
ParcoursPrefixe(a.gauche);
ParcoursPrefixe(a.droite);
afficher(racine);
}