Contenus
ToggleExercices corrigés sur les problèmes d'affectation
La page présente plusieurs exercices corrigés sur les problèmes de planification et d’ordonnancement automatisés, en particulier sur les problèmes d’affectation.

Exercice 1
Le réseau de la côte atlantique déssert quatre villes. La direction veut attribuer quatre usines aux villes. Le prix pour envoyer de l’énergie d’une usine à chaque ville est décrit ci-dessous :
Raleigh | Atlanta | Durham | Clemson | |
Plant A | 210 | 90 | 180 | 160 |
Plant B | 100 | 70 | 130 | 200 |
Plant C | 175 | 105 | 140 | 170 |
Plant D | 80 | 65 | 105 | 120 |
Une usine ne peut mériter qu’une seule ville, et une ville ne peut tirer des énergies que d’une seule usine. Trouvez la meilleure mission au moindre coût.
Après la première réduction :
R | A | D | C | |
A | 105 | 0 | 55 | 15 |
B | 15 | 0 | 25 | 75 |
C | 35 | 0 | 0 | 10 |
D | 0 | 0 | 5 | 0 |
Puis :
R | A | D | C | |
A | 90 | 0 | 40 | 0 |
B | 0 | 0 | 10 | 60 |
C | 55 | 15 | 0 | 10 |
D | 0 | 15 | 5 | 0 |
Solution : 90+100+140+120=450.
Exercice 2
| 8 | 16 | 15 | 91 | 64 |
| 83 | 42 | 93 | 75 | 27 |
| 76 | 95 | 75 | 81 | 50 |
| 20 | 42 | 96 | 90 | 24 |
| 38 | 28 | 2 | 15 | 81 |
Trouvez une solution d’affectation à cette matrice. Réorganisez les colonnes de façon à ce que la solution forme une diagonale.
Exercice 3
Trois robots {a,b,c} doivent terminer trois tâches {t1, t2, t3} dans la grille suivante. Il faut une journée à un robot pour passer d’une cellule à l’une de ses voisines.
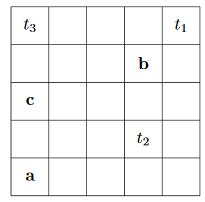
Dans le tableau suivant, nous listons les jours où chaque robot peut terminer chaque tâche seul. Les tâches doivent être terminées dès que possible.
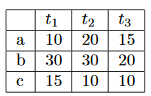
Ajoutez la distance de Manhattan en jours au dernier tableau. Résoudre le problème d’affectation.
Exercice 4
Braneast Airlines doit doter en personnel les vols défaillants entre New York et Chicago indiqués dans le tableau ci-dessous. Chacun des équipages de Braneast vit à New York ou à Chicago. Chaque jour, un équipage doit effectuer un vol NY-Chicago et un vol Chicago-NY avec au moins une heure d’arrêt entre les vols.
Braneast veut programmer les équipes pour minimiser le temps d’arrêt total. Élaborez un problème d’affectation qui peut être utilisé pour atteindre cet objectif. Bien sûr, certaines affectations ne sont pas possibles. Trouvez les affectations de vol qui minimisent le temps d’arrêt total. Combien d’équipages devraient être basés dans chaque ville ? Supposons qu’à la fin de la journée, chaque équipage doit être dans sa ville d’origine.
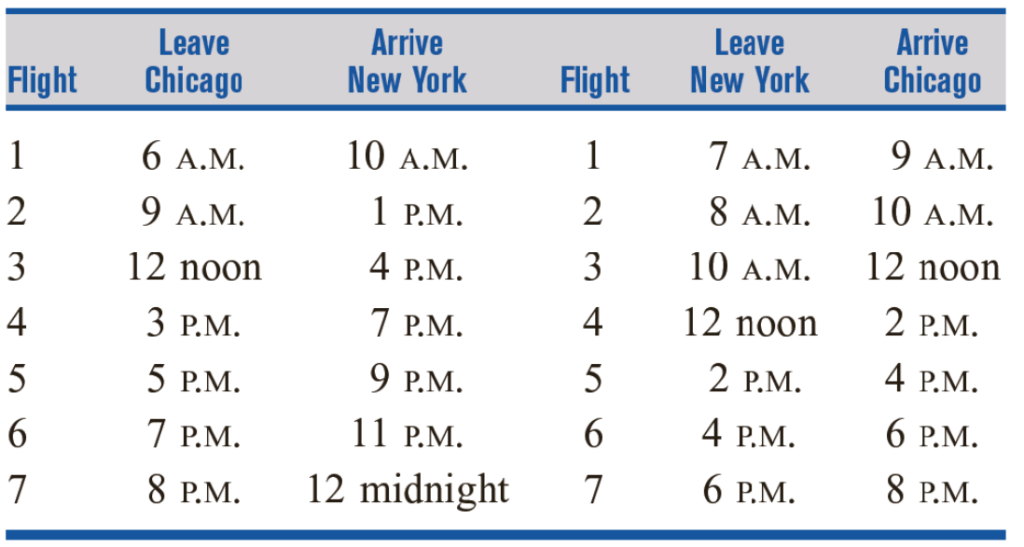
Le tableau d’affectation est construit comme suit : pour le premier vol au départ de Chicago, compte tenu de l’heure d’arrivée à NY, combien de temps l’équipage doit attendre à l’aéroport. Par exemple pour le premier vol de Chicago, il arrive à 10h :
Flight | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Leave New York | 7 | 8 | 10 | 12 | 14 | 16 | 18 |
Waiting time | impossible | impossible | impossible | 2 | 4 | 6 | 8 |
Nous notons que les vols 4, 5, 6, 7 de Chicago ne peuvent pas être le point de départ, nous calculons donc le temps d’attente depuis le vol de New York. Notez que le vol 7 de NY ne peut pas être un point de départ, nous calculons donc le temps d’attente depuis le vol de Chicago. De chacun des éléments du tableau, nous retenons la valeur la plus basse calculée (pour les vols depuis Chicago et NY).

Solution :

Commence à New York : (1,3), (2,4), (3,5), (5,6), (6,7).
Commence à Chicago : (4,1), (7,2).
Temps d’arrêt total = 25h.

Exercice 5
Considérez les données du tableau ci-dessous. Si un équipage basé à Mumbai arrive à Delhi sur un vol donné, il doit retourner à Mumbai sur un vol ultérieur. Supposons que pour tout appariement donné, l’équipage sera basé dans la ville qui entraîne la plus petite escale.
Le problème est de trouver les appariements de manière à minimiser le temps au sol loin du domicile, sous réserve d’un intervalle minimum d’une heure entre l’arrivée et le départ. Compte tenu des couples de vols, où les équipages doivent-ils être basés ?
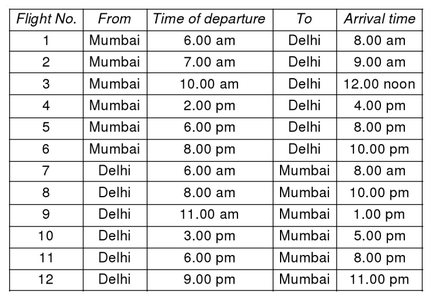
Comme dans l’exercice précédent, calculez d’abord les matrices de temps d’escale, l’une pour l’escale à Mumbai et l’autre pour Delhi.
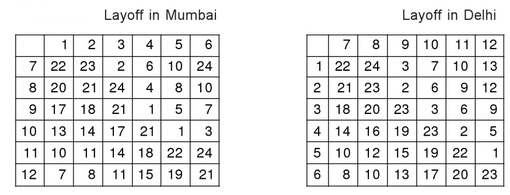
Nous calculons maintenant le minimum des valeurs pour les 36 paires et construisons le tableau ci-dessous. Par exemple (7,2) est le minimum entre (7,2) dans la première matrice et (2,7) dans la seconde.

La solution de ce problème est les paires (7,3) de Mumbai, (8,4) de Mumbai, (9,2) de Delhi, (10,5) de Mumbai, (11,6) de Delhi, (12, 1) depuis Delhi avec un temps d’arrêt total = 18h.
Exercice 6
Résoudre le problème suivant comme un problème d’affectation.
Minimiser 4X11+6X12+5X13+5X14+7X21+4X22+5X23+6X24 +4X31+7X32+6X33+4X34 +5X41+3X42+4X43+7X44
St. X11+X12+X13+X14=1
X21+X22+X24+X24=1
X31+X32+X33+X34=1
X41+X42+X43+X44=1
X11+X21+X31+X41=1
X12+X22+X32+X42=1
X13+X23+X33+X43=1
X14+X24+X34+X44=1
Vous devez résoudre le problème d’affectation :
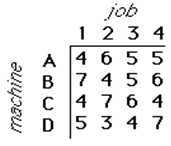
Exercice 7
Résoudre le problème suivant comme un problème d’affectation.

Le problème d’affectation est décrit dans le tableau ci-dessous :
1 | 2 | 3 | |
1 | 5 | 9 | inf |
2 | inf | 2 | inf |
3 | inf | 1 | 1 |
Exercice 8
Le Département d’histoire de l’art souhaite proposer six cours par semestre. Il y a sept professeurs dans le département, dont chacun ne peut enseigner que certains cours, comme indiqué dans le tableau. Est-il possible d’attribuer les six cours aux professeurs afin qu’aucun professeur n’enseigne plus d’un cours ?
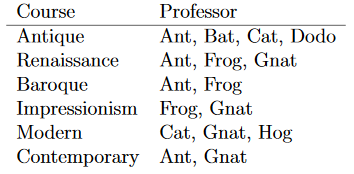
Le problème d’affectation est décrit dans le tableau ci-dessous :
Ant | Bat | Cat | Dodo | Frog | Gnat | Hog | |
Antique | 1 | 1 | 1 | 1 | inf | inf | inf |
Renaissance | 1 | inf | inf | inf | 1 | 1 | inf |
Baroque | 1 | inf | inf | inf | 1 | inf | inf |
Impressionism | inf | inf | inf | inf | 1 | 1 | inf |
Modern | inf | inf | 1 | inf | inf | 1 | 1 |
Contemporary | 1 | inf | inf | inf | inf | 1 | inf |
dummy | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Afin de trouver une mission, il est préférable d’utiliser la méthode du stepping stone au lieu de la méthode hongroise.
