Exercice 1
Une entreprise doit transporter des fournitures des usines aux chantiers de construction. Les trois usines ont respectivement une capacité d’approvisionnement de 300, 300, 100. Et les trois chantiers en demandent respectivement 200, 200, 300.
Les frais de transport sont indiqués dans le graphique suivant :
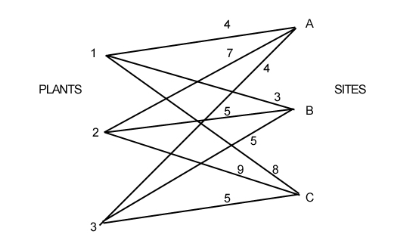
Trouvez comment répartir les fournitures.
Résoudre le problème de planification suivant avec l’algorithme de Stepping Stone.
Exercice 2
Le blé est récolté dans le Midwest et stocké dans des élévateurs à grains dans trois villes différentes : Kansas City, Omaha et Des Moines. Ces élévateurs à grain alimentent trois minoteries situées à Chicago, St. Louis et Cincinnati. Le grain est expédié aux moulins dans des wagons de chemin de fer, chaque wagon pouvant contenir une tonne de blé. Chaque élévateur à grains est en mesure de fournir le nombre suivant de tonnes (c’est-à-dire de wagons de chemin de fer) de blé aux moulins sur une base mensuelle.
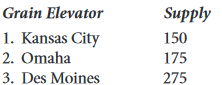
Chaque moulin demande le nombre suivant de tonnes de blé par mois.
Le coût de transport d’une tonne de blé de chaque élévateur à grains (source) à chaque moulin (destination) diffère selon la distance et le système ferroviaire. Ces coûts sont indiqués dans le tableau suivant. Par exemple, le coût d’expédition d’une tonne de blé de l’élévateur à grains d’Omaha au moulin de Chicago est de 7 $.
Le problème est de déterminer le nombre de tonnes de blé à transporter de chaque élévateur à grain à chaque moulin sur une base mensuelle afin de minimiser le coût total du transport. Existe-t-il une solution alternative ? Si oui, lequel ?
Exercice 3
À partir du programme linéaire ci-dessous, formulez le problème de transport et résolvez-le.
Existe-t-il une solution alternative ? Si oui, lequel ?
Le programme linéaire correspond à l’exercice 2.
Exercice 4
Prenez le même problème qu’à l’exercice 2. Changez la demande à Cincinnati à 350 tonnes. Résoudre.
Voici le tableau à résoudre :
Exercice 5
Résolvez le problème LP suivant :
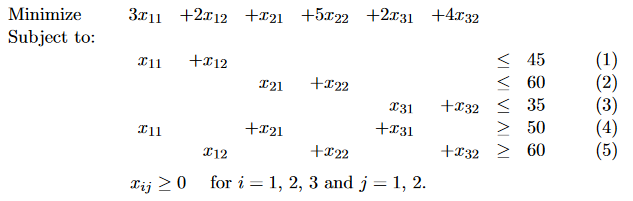
Nous introduisons une variable muette pour j car offre(45+60+35)-demande(50+60)=30 :
Exercice 6
La Conférence de la côte atlantique organise quatre matchs de basket-ball lors d’une soirée particulière. Le bureau de la conférence veut affecter quatre équipes d’officiels aux quatre matchs de manière à minimiser la distance totale parcourue par les officiels. Les distances en miles de chaque équipe d’officiels à chaque lieu de match sont indiquées dans le tableau ci-dessous :
Chaque offre et chaque demande sont égales à 1. Résolvez-le comme un problème de transport.
FR 
EN 
ES