Contenus
ToggleAlgorithme de McNaughton et Yamada
L’algorithme de McNaughton et Yamada suit les étapes suivantes. Étant donné un automate à n états, et dont les états sont numérotés de 1 à n, on donne une expression pour les langages composés des mots qui étiquettent les chemins de i à j, pour tout couple i, j. Cette expression est construite par récurrence au moyen d’une condition sur les chemins. Cette condition stipule que les chemins ne passent que par certains états autorisés.
Notre automate ayant n états, nous nous concentrons donc sur la construction d’une expression régulière pour chacun des n×n langages Ls,s’ = { w∈X* | s.w = s‘ } formé de tous les mots qui envoient un état s quelconque sur un autre état s’. Si nous y parvenons, le langage reconnu par l’automate sera la valeur d’une réunion finie d’expression régulières donc d’une expression régulière.
L’idée est de procéder pas à pas en prenant en compte un nombre croissant d’états intermédiaires entre s et s’. Les états étant supposés numérotés de 0 à n, on commence par aucun état intermédiaire, puis seulement s0, puis s0 et s1, puis s0, s1 et s2, etc.
On note Ls,s’(k) est l’expression pour l’ensemble des mots qui étiquettent des chemins de s à s’ et dont tous les sommets intermédiaires sont inférieurs ou égaux à k. Les sommets de départ s et d’arrivée s’ ne sont pas intermédiaires, donc ils ne sont pas soumis à la contrainte d’être inférieurs ou égaux à k.
On construit les Ls,s’(k) par récurrence sur k, en commençant avec k=0, et en terminant avec k=n. Lorsque k=n, la contrainte sur k n’est plus une restriction, et Ls,s’(k)=Ls,s’ si s≠s’, et ε+Ls,s(n)=Ls,s.
Pour k=0, comme les sommets sont numérotés à partir de 1, la contrainte exprime simplement qu’il n’y a pas de sommet intermédiaire. Les seuls chemins sont des transitions de s à s’ (on ignore un chemin de longueur 0 en un état s).
On a donc avec s=p et s’=q :
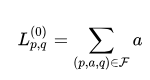
Pour la récurrence, on considère un chemin de s à s’ dont les sommets intermédiaires sont plus petits que k. Deux cas sont alors possibles :
- les sommets intermédiaires sont plus petits que k-1, alors l’étiquette est dans Ls,s’(k-1)
- le chemin passe par l’état k. On décompose alors le chemin en parties dont les sommets intermédiaires sont plus petits que k-1. Pour cela, on considère chaque occurrence du sommet k dans ce chemin : entre deux occurrences consécutives, les sommets intermédiaires sont plus petits que k-1. On a alors la formule avec s=p et s’=q :
 .
.
Il y a donc n+1 étapes. Chacune des étapes demande le calcul de n² expressions, et la taille des expressions elles-mêmes croît avec k.
Exemple
Prenons l’automate suivant :

Avec k=0 nous avons :
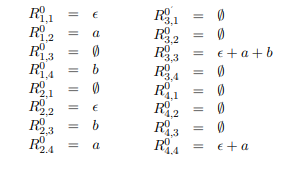
Puis k=1 :
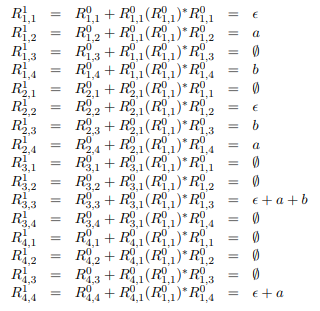
Puis k=2 :
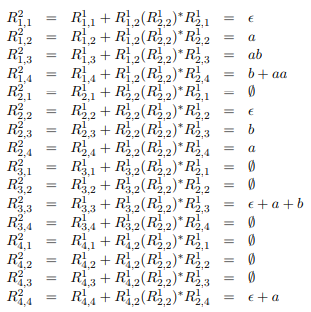
Puis k=3 :

Pour la dernière étape on se contente de calculer les deux expressions qui nous intéressent (états initiaux vers états finaux) :

L’expression voulue est donc ab(a + b)∗ + (b + aa)a∗.
