Automate fini déterministe

Difficulté

Facile 25%

Contenus

On a l’habitude de dessiner un automate fini déterministe, en figurant les états par des cercles, en indiquant l’état initial par une flèche entrante, les états acceptants par un double cercle ou une flèche sortante, et la transition de l’état q à l’état q’ en lisant la lettre α par une flèche allant de q vers q’ et étiquetée par α.

Un automate fini déterministe A est un triplet (Vt, Q, T) où

Vt est le vocabulaire de l’automate ;
Q est l’ensemble fini des états de l’automate ;
T : Q × Vt → Q, est une application partielle appelée fonction de transition de l’automate.

Lorsque T est totale, autrement dit s’il y a dans chaque état exactement une transition pour toute lettre de l’alphabet, l’automate est dit complet.

Lecture d’un mot

Notons que les dérivations produit par la lecture d’un mot w par un automate fini déterministe est linéaire et se trouve donc exempte d’ambiguïté : la lecture des lettres composant le mot provoque des transitions bien définies jusqu’à être bloqué en cas de transitions manquantes, ou bien jusqu’à atteindre un certain état après la lecture complète du mot. Pour vérifier la lecture d’un mot, il faut partir des états initiaux et consommer un par un les symboles en se déplaçant dans l’automate jusqu’à avoir un cas impossible ou bien la lecture complète du mot.

On en déduit la propriété fondamentale des automates déterministes complets :

Soit A = (Vt, Q, T) un automate fini déterministe complet. Alors, pour tout mot u ∈ V^∗_t et tout état q ∈ Q, il existe un unique état q’ ∈ Q tel que q(u)→Aq’.

En pratique, il peut être utile de rendre un automate complet en ajoutant un nouvel état appelé poubelle vers lequel vont toutes les transitions manquantes. Les calculs bloquants aboutissent alors dans la poubelle où ils restent capturés.

Un automate déterministe peut aussi être défini avec deux données supplémentaires :

d’un état initial i ∈ Q ;
d’un ensemble d’états acceptants F ⊆ Q ;

Notons que l’état initial et les états acceptants peuvent aussi être déduit des règles T.

Un mot w est reconnu par l’automate s’il existe un calcul dit réussi issu de l’état initial i et terminant en état acceptant après avoir lu le mot w. On note par L(A) le langage des mots reconnus par l’automate A. Un langage reconnu par un automate est dit reconnaissable. On note par Rec l’ensemble des langages reconnaissables. L’ajout d’un état poubelle ne change pas les mots reconnus par un automate.

Du langage à l’automate

Tout langage accepté par un automate fini est régulier. Tout langage régulier est accepté par un automate fini.

Pour chacun des langages ci-dessous, expliciter le langage et dessiner un automate déterministe qui le reconnait.

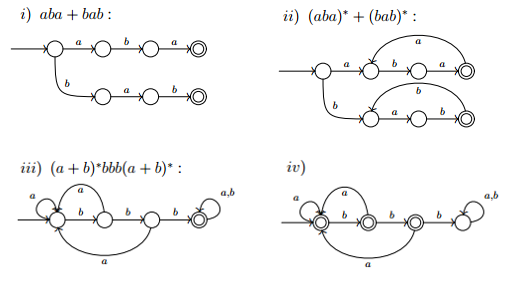
L est le langage dénoté par aba + bab.
L est le langage dénoté par (aba)^∗ + (bab)^∗.
L = {u ∈ {a, b}^∗ tel que u contient le facteur bbb}.
L = {u ∈ {a, b}^∗ tel que u ne contient pas le facteur bbb

On peut transformer de manière effective une grammaire régulière à droite en automate fini déterministe et vice versa. Les non-terminaux correspondent aux états de l’automate.

Des automates aux mots reconnus

Donner tous les mots de longueur 0, 1, 2, 3 et 4 reconnus par les automates suivants. Il est possible de répondre à cette question de manière systématique en utilisant les matrices. Pour cela, on représente l’automate (que l’on peut voir comme un graphe) par la matrice d’adjacence. Ainsi, le coefficient d’indice i, j de la matrice M^k correspond aux mots de longueur k reconnus par l’automate, si l’état initial était l’état i et l’état final, l’état j. Si l’on souhaite obtenir les mots de longueur k reconnus par notre automate, il suffit de multiplier la matrice par elle-même.

On peut symboliser (et même stocker) les transitions d’un automate fini sous la forme d’un tableau à deux dimensions. Les lignes représentent les états de départs de transitions, les colonnes indiquent les symboles et les valeurs les états de destination de la transition.

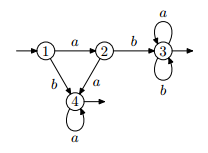
Pour l’automate A, il suffit d’évaluer (1,3) et (1,4) des matrices suivantes – en effet les mots reconnus commencent à l’état 1 et finissent en l’état 3 ou 4 :

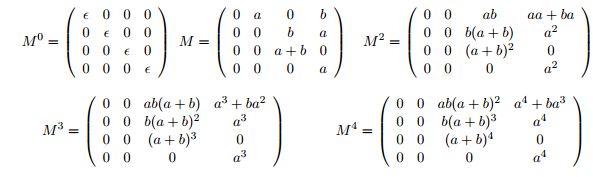
Mots de longueurs 0 : aucun ; Mots de longueurs 1 : b ; Mots de longueurs 2 : ab + aa + ba ; Mots de longueurs 3 : aba + abb + aaa + baa ; Mots de longueurs 4 : abaa + abab + abba + abbb + aaaa + baaa.