Contenus
ToggleConstruction de Thompson
L’algorithme de Thompson ou construction de Thompson permet de construire un automate non-déterministe avec epsilon-transition à partir d’une expression régulière. L’automate se construit récursivement à partir de motifs de base :
Les éléments unitaires comme ∅, ε et a sont reconnus par
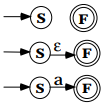
On considère les opérateurs de l’expression régulière R selon l’ordre d’extériorité décroissant. L’opérateur le plus extérieur permet de découper R en R1 | R2 , R1.R2 ou R1* qui sont reconnus par

Voici un exemple de construction avec l’expression (a|b)(a∗|ba∗|b∗)∗
On commence la récursion par la création de (A)(B) – le contenu n’est qu’à titre indicatif, nous verrons comment remplir A et B au fur et à mesure.

Puis par la mise en place de l’étoile sur (B)* – ici on en profite pour faire le fonction OU dans (A) = (a|b).

La prochaine étape consiste à faire la fonction OU dans (B)=(C|D|E)
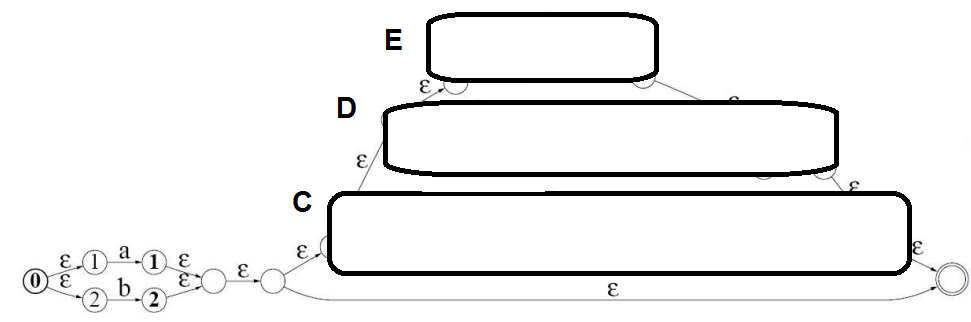
Le processus contenu en descendant récursivement jusqu’à l’obtention de l’automate de Thompson final.
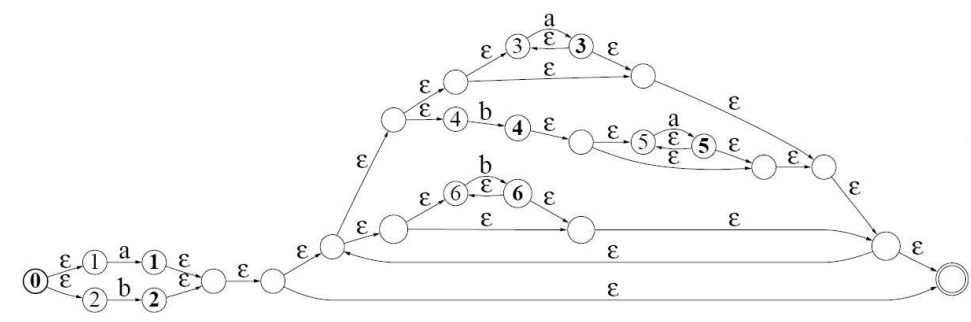
Ce dernier devra alors être déterminisé et minimiser pour une meilleur lecture.
Quelques exemples simples
- 01∗
- (0 + 1)01
- 00(0 + 1)*