Contenus
ToggleAFI vers AFD
Le théorème de Rabin-Scott dit que tout langage reconnu par un automate fini indéterministe peut être reconnu par un automate fini déterministe (déterminisation AFI vers AFD). Il est donc possible de représenter un automate indéterministe par un automate déterministe, ce processus s’appelle la déterminisation.
Considérons par exemple l’automate fini non-déterministe (K, T, M, I, F) suivant :
K = {S1, S2, S3, S4}
T = {a, b, c}
M = {(S1, a, S1),(S1, a, S3),(S2, b, S2),(S2, b, S3),(S3, c, S3),(S3, c, S4)}
I = {S1, S2}
F = {S4}
correspondant au graphe suivant :
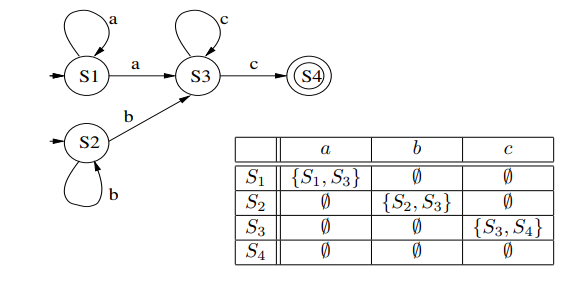
On construit ensuite les états de l’automate fini déterministe (AFD) et leur fonction de transition. Au départ, il a un seul état qui est composé de l’ensemble des états initiaux de l’automate fini indéterministe (AFI): sur notre exemple, l’état initial de l’AFD est {S1, S2}.
A chaque fois qu’on ajoute un nouvel état dans l’AFD, on détermine sa fonction de transition en faisant l’union des lignes correspondantes dans la table de transition de
l’AFI : sur notre exemple, pour l’état {S1, S2}, on fait l’union des lignes correspondant à S1 et S2, et on détermine la fonction de transition

Autrement dit, quand on est dans l’état “S1 ou S2″ et qu’on lit un a, on va dans l’état “S1 ou S3″ (M({S1, S2}, a) = {S1, S3}), quand on est dans l’état “S1 ou S2″ et qu’on lit un b, on va dans l’état “S2 ou S3″ (M({S1, S2}, b) = {S2, S3}) et quand on est dans l’état “S1 ou S2″ et qu’on lit un c, on va dans l’état “vide », correspondant à l’état d’erreur (M({S1, S2}, c) = ∅.
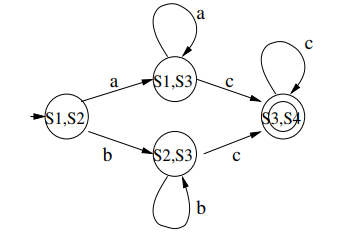
On rajoute ensuite les états {S1, S3} et {S2, S3} à l’AFD et on détermine leur fonction de transition selon le même principe. De proche en proche, on construit la table de transition suivante pour l’AFD :

L’ensemble des états de l’AFD est K’ = {{S1, S2}, {S1, S3}, {S2, S3}, {S3, S4}}. Les états de l’AFD contenant un état final de l’AFI sont des états finaux. Ici, l’AFI a un seul état final S4 et l’ensemble des états finaux de l’AFD est F’ = {{S3, S4}}. Cet AFD correspond au graphe suivant :
Autre exemple
Voici un autre exemple de déterminisation AFI vers AFD.
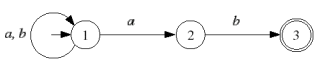
Pratiquement, on ne construit que les états accessibles à partir de I, de proche en proche : on part de l’état initial I, puis on calcule toutes les transitions qui partent de I, puis on recommence avec les nouveaux états obtenus, etc.
N.B : la méthode du cours est aussi valable pour les TDs et le projet. Vous utilisez celle que vous comprenez le mieux ! Vous avez le même exemple avec les notations du cours après cette méthode.
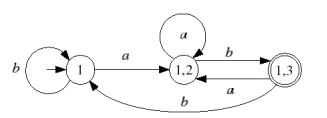
état initial : I = {1} transition par a : {1, 2} transition par b : {1} . On vient de faire {1} donc on va faire {1,2}
état {1, 2} transition par a : {1, 2} transition par b : {1, 3}, on fait maintenant {1,3}
état {1, 3} transition par a : {1, 2} transition par b : {1}. Il ne reste aucun état non visité. Seul l’état {1,3} contient un état terminal, {1,3} est donc terminal.
Ce qui nous donne le DFA suivant :
Le calcul par les tableaux est beaucoup plus lisible.
| delta | a | b |
| 1 | {1,2} | {1} |
| 2 | – | {3} |
| 3 | – | – |
Calculons les états de delta prime :
| Detla prime | a | b |
| 1 | {1,2} | 1 |
| 1,2 | {1,2} | {1,3} |
| {1,3} | {1,2} | {1} |
La deuxième ligne nous crée l’état {1,3}. Nous remarquons qu’à la fin, l’automate est le même que celui calculer avec la méthode précédente (l’état 3 n’est pas utile puisque personne ne l’appelle).
