Contenus
ToggleExercices corrigés sur la théorie des langages, automates et grammaires
Exercices corrigés sur la théorie des langages, les automates et les grammaires. Les exercices sont suivis d’une correction.

Mots reconnus
Exercice 1
Donner tous les mots de tailles 0, 1, 2, 3, et 4 des langages réguliers suivants : (a + ba)* ; a(aa + b(ab) ∗a)∗a. Pour cela, vous pouvez faire un arbre de possibilité pour chacun des langages.
Mots de longueurs 0 : epsilon ; Mots de longueurs 1 : a ; Mots de longueurs 2 : aa, ba ; Mots de longueurs 3 : aaa, aba, baa ; Mots de longueurs 4 : aaaa, aaba, abaa, baba, baaa.
Mots de longueurs 0 : aucun ; Mots de longueurs 1 : aucun ; Mots de longueurs 2 : aa ; Mots de longueurs 3 : aucun ; Mots de longueurs 4 : aaaa, abaa.
Exercice 2
Donner tous les mots de longueur 0, 1, 2, 3 et 4 reconnus par les automates suivants. Il est possible de répondre à cette question de manière systématique en utilisant les matrices. Pour cela, on représente l’automate (que l’on peut voir comme un graphe) par la matrice d’adjacence. Ainsi, le coefficient d’indice i, j de la matrice Mk correspond aux mots de longueur k reconnus par l’automate, si l’état initial était l’état i et l’état final, l’état j. Si l’on souhaite obtenir les mots de longueur k reconnus par notre automate, il suffit de multiplier la matrice par elle-même.

Pour l’automate A1, il suffit d’évaluer (1,3) et (1,4) des matrices suivantes :
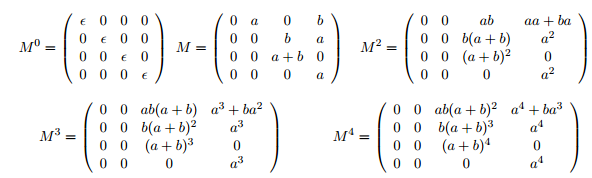
Mots de longueurs 0 : aucun ; Mots de longueurs 1 : b ; Mots de longueurs 2 : ab + aa + ba ; Mots de longueurs 3 : aba + abb + aaa + baa ; Mots de longueurs 4 : abaa + abab + abba + abbb + aaaa + baaa.
Pour l’automate A1, il suffit d’évaluer (1,1) et (1,2) des matrices suivantes :
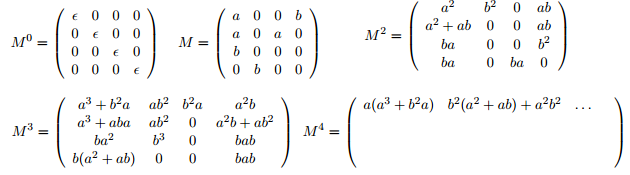
Mots de longueur 0 : M0 1,1 + M0 1,2 = ; Mots de longueur 1 : M1 1,1 + M1 1,2 = a ; Mots de longueur 2 : M2 1,1 + M2 1,2 = aa + bb ; Mots de longueur 3 : M3 1,1 + M3 1,2 = aaa + bba + abb ; Mots de longueur 4 : M4 1,1 + M4 1,2 = aaaa + abba + aabb + bbaa + bbab
Exercice 3
Soit l’automate M suivant :

Combien d’états possède l’automate M ? Donner l’ensemble des états finaux, et l’ensemble des états
Initiaux. L’automate est-il déterministe ? Dans quel état se trouve l’automate après avoir lu le mot bbabbb ? Ce mot est-il reconnu par l’automate / accepté par l’automate ? Mêmes questions pour le mot babaabba.
Rendre l’automate M complet. Le mot baa est-il reconnu par cet automate ? accepté par cet automate ?
Soit l’automate N suivant :

Dans quels états peut être l’automate N après avoir lu babba ? Ce mot est-il accepté par cet automate ? Même question pour le mot abbb.
Les premières questions demandent une description formelle de l’automate M. Lorsqu’on construit la table de transition, on remarque que l’automate M et déterministe contrairement à l’automate N. Pour compléter M, il faut rajouter l’état poubelle, tous les mots sont reconnus mais le langage accepté reste le même que non complet.
Pour lire le premier mot : 1 ⊢ b1 ⊢ bb1 ⊢ bba2 ⊢ bbab3 ⊢ bbabb4 ⊢ bbabbb2 or 2 n’est pas un état final donc il est reconnu mais pas accepté. Le principe de dérivation est le même si l’automate est déterministe, sinon il faut créer un arbre de dérivation.
Pour lire le dernier mot :
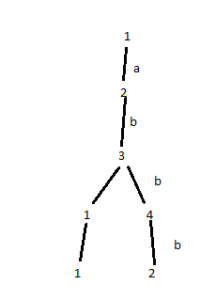
On remarque que l’automate peut lire le mot abbb de deux façons, lorsqu’un mot ne peut plus être lu dans une branche on note # et la branche se termine.
Construction d’automate
Exercice 4
Pour chacun des langages ci-dessous, expliciter le langage et dessiner un automate qui le reconnait à l’aide d’une méthode de construction.
- L est le langage dénoté par aba + bab.
- L est le langage dénoté par (aba)∗+ (bab)∗.
- L = {u ∈{a, b}∗ tel que u contient le facteur bbb}.
- L = {u ∈{a, b}∗ tel que u ne contient pas le facteur bbb
Exercice 5
Construire avec la méthode de votre choix les automates reconnaissants les langages suivant (écrivez l’expression rationnelle dénotant ces langages) :
- Le langage des mots contenant au moins une fois la lettre a
- Le langage des mots contenant au plus une fois la lettre a
- Le langage des mots contenant un nombre pair de fois la lettre a
- Le langage des mots admettant aba pour facteur
Langage reconnu
Exercice 6
Avec la méthode de votre choix, déterminer le langage reconnu par les automates suivant :

Exercice 7
Soit la grammaire G = ({a, b, c} , {S, A} , S , P) ; où P contient les règles suivantes : S → aS | bA ; A → cA | ε
Déterminer si les mots w1 = abac, w2 = aabccc, w3 = cabbac et w4 = ab sont générés par G. Trouver le langage généré par G (qu’on note L(G)).
Les mot w1 et w3 ne sont pas générés par G ; les mots w2 et w4 sont générés par G : S ⊢ aS ⊢ aaS ⊢ aabA ⊢ aabcA ⊢ aabccA ⊢ aabcccA ⊢ w2 et pour w4 : S ⊢ aS ⊢ abA ⊢ ab = w4.
Pour trouver le langage, écrivez l’automate engendré par la grammaire puis utiliser la méthode de votre choix pour obtenir son expression régulière : a* bc*.
Exercice 8
Soit la grammaire g = <{a, b, c}, {S, A, B}, S, P> où : P = { S → aA | ε ; A → bA | cB ; B → bB | a }.
Trouver le système d’équations (d’expressions régulières) correspondant. Résoudre ce système.
On va associer une variable à chaque non terminal de g : X0 (associé à S), X1 (à A) et X2 (à B). On traduit les règles de productions de P en équations d’expressions régulières :

En appliquant le théorème d’Arden à la 3ième équation, on obtient : X2 = b*a. En remplaçant X2 dans la 2ième équation on aura : X1 = b.X1 + cb*a ; puis avec le théorème d’Arden on obtient : X1 = b*cb*a. On remplace dans la première équation et on aura : X0 = ab*cb*a + ε qui dénote le langage engendré par g.
Exercice 9
Soit la grammaire g = <{a, b, c}, {S, A, B}, S, P> où : P = { S → baA | aS | ε ; A → aA | bB | ε ; B → cB | aA }.
Construire l’automate d’états finis simple A équivalent à g. Ecrire le système d’équations associé à A. Trouver l’expression régulière qui dénote L(A).
Pour trouver l’automate simple associé à g, on peut décomposer la règle S → baA en deux règles : S → bC et C → aA ; ou C est un nouveau non terminal. On construit l’automate simple A équivalent en associant un état de l’automate à chaque non-terminal, cet état sera final lorsque le non-terminal associé produit ε. Les transitions de A seront déduites à partir des règles de productions de g.
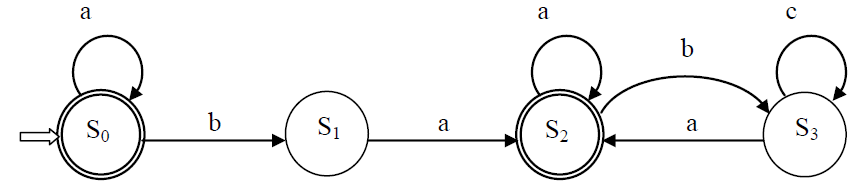
Le système d’équations régulières associé à A :
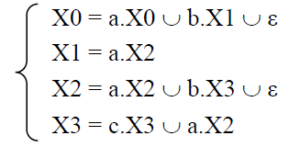
Pour trouver l’expression régulière qui dénote L(A), on résout le système pour trouver la valeur de X0. De la quatrième équation on a : X3 = c*aX2 ; on remplace dans la troisième : X2 = aX2 +bc*aX2 + ε = (a +bc*a)X2 +ε qui se résout avec X2 = (a +bc*a)*. On remplace dans la deuxième : X1 = a(a +bc*a)*. Puis dans la première : X0 = aX0 +ba(a + bc*a)* + ε. Et on obtient ainsi la solution : X0 = a*(ba(a +bc*a)* +ε). Donc L(A) est dénoté par l’expression régulière : a*ba(a+ bc*a)* +a*.




