L’algorithme de Google PageRank, qui est le centre de la recherche Google, est basé sur les chaînes de Markov, en voici son explication (pour la version basique).

Contenus
ToggleLa naissance de Google PageRank
Avec 1 milliard de sites sur internet, c’est impossible à analyser leurs contenus. Pourtant, l’internet n’est pas une collection de textes indépendants mais un immense hypertexte : les pages se citent mutuellement. En considérant le web comme un graphe et en tenant compte les liens entre les pages, on peut faire des choses intéressantes. Les premières personnes qui ont abordé ce point de vue étaient Larry Page et Sergey Brin, fondateurs de Google, avec leur algorithme PageRank.
Depuis sa conception en 1998, Google domine le marché des moteurs de recherche sur internet. 17 ans plus tard, leurs techniques ont déjà beaucoup évolué, les résultats de recherche deviennent de plus en plus pertinents, mais l’idée principale est toujours basée sur l’algorithme de classer PageRank. Dans cet article, on va examiner de plus près cet algorithme et le lien avec la chaîne de Markov.
PageRank utilise une fonction qui assigne une valeur à chaque page sur internet. Plus la valeur est élevée, plus la page est importante.
PageRank est un algorithme qui est indépendant de la requête et du contenu. L’indépendance de la requête veux dire que le classement des sites est effectué hors-ligne. En effet, chaque 30 jours, Google télécharge, indexe et classe tous les sites. Par conséquent, le classement des résultats ne dépend pas de la requête. L’indépendance du contenu est assez claire vu qu’elle est abordée dans la partie Introduction : l’algorithme PageRank n’utilise pas les contenus mais les liens pour classer les pages.
La majorité d’entre eux classe les résultats en basant sur la fréquence dont le mot cherché est utilisé sur chaque site. Cela vite révélait des problèmes : si un site veut attirer des visiteurs, il faut juste spammer les mots-clés et le moteur de recherche va croire que c’est un résultat vraiment pertinent.
Les techniques pour berner les moteurs de recherche comme celle-ci sont appelées « term spam ». Pour éviter ces fraudes, Larry Page et Sergey Brin ont crée PageRank avec 2 innovations :
— PageRank simule d’une marche aléatoire d’un visiteur, qui choisit par hasard un lien sur la page actuelle pour passer à la prochaine page. Ce processus se répète plusieurs fois et les auteurs raisonnent que les pages sur lesquels l’utilisateur passe plus de temps sont plus important que ceux que l’utilisateur visite rarement.
— L’importance d’une page dépend de l’importance des pages qui
entrainent à celle-ci. Alors même si quelqu’un a crée 1000 pages fausses contenant des liens à la page principale, le rang PageRank de cette page principale n’est pas beaucoup amélioré parce que ces 1000 pages fausses sont pas « importantes ».
À ce moment là, Page et Brin n’ont pas encore abordé le terme « Markov » dans leur article, mais on peut remarquer facilement que la modélisation de la marche aléatoire est une chaine de Markov. Encore plus intéressant, la probabilité stationnaire d’une chaine de Markov nous donne une idée de la proportion de temps que Xn va passer à chaque état en long terme.
Alors si la chaine converge vers sa probabilité stationnaire, sa probabilité limite est effectivement le rang PageRank cherché. En d’autre termes, l’algorithme PageRank calcule le rang de chaque site en cherchant la probabilité stationnaire unique de la chaine de Markov.
Mais la vie n’est pas si simple. On ne peut pas assurer que notre chaine de Markov converge, ou qu’il existe une unique probabilité stationnaire. C’est souvent le cas pour un modèle de l’internet. Par exemple, c’est très peu probable que les sites de Maths aient des liens avec des sites de Sport (oui parce que les geeks ne font pas du sport …), et donc notre chaine de Markov a 2 classes finaux, d’où 2 probabilités stationnaires.
Afin de régler ce problème, Page et Brin essaient de construire une chaine de Markov ergodique, ce qui va assurer l’existence d’une unique probabilité stationnaire, ce qui devient dont le vecteur PageRank.
Exemple
Soit Xn la page que l’utilisateur visite à l’étape n. Xn peut être modélisé par une chaine de Markov car le choix de l’utilisateur dépend seulement de la page actuelle.
Supposant que notre « Internet » est composé de 7 pages, qui sont représentées comme les 7 nœuds. Les arêtes représentent les liens entre les pages. Etant sur une page, un visiteur choisit aléatoirement un lien pour aller à une autre page, alors les probabilités d’aller d’une page aux autres sont égaux.

La matrice de transition est :

On observe qu’il existe 2 états absorbants : 4 et 7. La chaine n’est pas ergodique, elle possède 2 probabilités stationnaires et donc elle ne converge pas vers une probabilité unique.
Pour éviter cette situation, Page et Brin ont fait une hypothèse :
Une fois que le visiteur tombe sur une page « finale » (ie. pas de lien pour s’en sortir), il va aller sur la barre d’adresse et taper l’adresse d’un site aléatoire.
En terme de matrice de transition, on va remplacer la colonne de l’état absorbant par le vecteur :
![]()
La matrice de transition T devient donc :

Avec ce changement, T est irréductible et apériodique, donc ergodique. Pourtant, ce n’est pas toujours le cas, prenant l’exemple avec les sites de Maths et les sites de Sport, on peut obtenir une matrice de transition T :

Elle n’a pas des états absorbantes mais elle n’est pas irréductible et donc pas ergodique. Il faut que l’on fasse encore une autre hypothèse :
Supposant que le visiteur est sur une page, on dit qu’avec la probabilité p il va choisir un des liens dans cette page et avec la probabilité 1 − p il va aller sur la barre d’adresse et taper l’adresse d’un site aléatoire.
La nouvelle matrice de transition est donc :
G = pT + (p − 1)K
avec K la matrice dont chaque colonne est le vecteur :
![]()
La matrice G est appelée la matrice de Google. G est ergodique. Google utilise souvent p = 0.85.
En appliquant à notre exemple, on obtient :

En résolvant Gπ = π, on trouve :
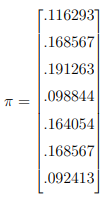
L’ordre de classement dans notre exemple est donc : 3,2,6,5,1,4,7. Alors si un mot cherché apparait dans les pages 1,2,5, l’ordre des résultats est 2,5,1.
Casser le système
Si la valeur PageRank (qui est aussi la probabilité stationnaire) d’une page est p, le temps de retour de cette page est 1/p. Alors on peut effectivement augmenter la valeur PageRank en diminuant le temps de retours, ce qui est possible si on crée des cycles très courts, ou idéalement des loops.
Concrètement, pour une page x, on supprime tous les liens sur celle-ci (ie. pas de sortie), on crée une autre page, y, avec seulement 2 arêtes x → y et y → x. La valeur PageRank de la page x augmente car chaque fois que le visiteur tombe sur cette page, il peut pas s’en sortir. Comme on a discuté dans la partie 3 (avec l’exemple de Maths et Sport), l’algorithme de PageRank peut éviter l’effet de cette stratégie en augmentant la valeur de p, la probabilité que le visiteur va aller sur la barre d’adresse et taper l’adresse d’un site aléatoire.
Une autre stratégie est de créer beaucoup de pages qui a seulement 1 arête vers la page x. Cette technique profite la probabilité p de recommencer la marche. Si on a une très grande nombre de pages fausses, c’est très probable que après recommencer, on va tomber sur la page x, et donc la valeur PageRank augmente. Pour éviter cette situation, il faut diminuer la valeur de p.
Grâce à ces 2 situations on voit bien que le choix de p est extrêmement important pour éviter les spams. Si p est trop élevée, les spammers doivent juste créer des millions de pages fausses entrainant à leurs pages principales. En revanche, avec une très petite p, ils peuvent établir des loops avec leur pages.
Ce que l’on a discuté est seulement les principes de bases de la moteur de recherche de Google. Les techniques ont déja beaucoup très évolué pour donner les résultats plus pertinents. La question de computation est très intéressante aussi. Etant donné que la vraie matrice de Google est de taille 8 milliards x 8 milliars, la méthode d’élimination de Gauss n’est pas pratique. On utilise des algorithmes plus puissants pour trouver les vecteurs propres, notamment la méthode de la puissance.
