The Google PageRank algorithm, which is the center of Google search, is based on Markov chains, here is its explanation (for the basic version).

Contents
ToggleThe birth of Google PageRank
With 1 billion sites on the internet, it is impossible to analyze their content. However, the Internet is not a collection of independent texts but an immense hypertext: the pages cite each other. Considering the web as a graph and by taking into account the links between the pages, we can do interesting things. The first people who addressed this point of view were Larry Page and Sergey Brin, founders of Google, with their algorithm PageRank.
Since its conception in 1998, Google has dominated the internet search engine market. 17 years later, their techniques have already evolved a lot, the search results are becoming more and more relevant, but the main idea is still based on the algorithm to rank PageRank. In this article, we will take a closer look at this algorithm and the link with the Markov chain. markov chain.
PageRank uses a function that assigns a value to every page on the internet. The higher the value, the more important the page.
PageRank is an algorithm that is independent of query and content. Query independence means that the ranking of sites is done offline. Indeed, every 30 days, Google downloads, indexes and ranks all sites. Therefore, the ranking of results does not depend on the query. The independence of the content is quite clear since it is discussed in the Introduction part: the PageRank algorithm does not use the contents but the links to rank the pages.
The majority of them rank results based on how often the search word is used on each site. This quickly revealed problems: if a site wants to attract visitors, you just have to spam the keywords and the search engine will believe that it is a really relevant result.
Techniques to trick search engines like this are called "term spam." To avoid these frauds, Larry Page and Sergey Brin created PageRank with 2 innovations:
— PageRank simulates a random walk of a visitor, who randomly chooses a link on the current page to move to the next page. This process is repeated several times and the authors reason that the pages on which the user spends more time are more important than those which the user rarely visits.
— The importance of a page depends on the importance of the pages that
lead to this. So even if someone has created 1000 bogus pages containing links to the main page, the PageRank of that main page is not much improved because those 1000 bogus pages are not “important”.
At this time, Page and Brin have not yet addressed the term "Markov" in their article, but one can easily notice that the modeling of the random walk is a Markov chain. Even more interesting, the stationary probability of a Markov chain gives us an idea of the proportion of time that Xn will spend in each state in the long term.
Then if the chain converges towards its stationary probability, its limiting probability is indeed the sought PageRank. In other words, the PageRank algorithm calculates the rank of each site by finding the unique stationary probability of the Markov chain.
But life is not that simple. We cannot ensure that our Markov chain converges, or that there is a unique stationary probability. This is often the case for an internet model. For example, it's very unlikely that Maths sites have links to Sports sites (yes because geeks don't do sports…), and so our Markov chain has 2 final classes, hence 2 stationary probabilities.
In order to solve this problem, Page and Brin try to construct a Markov chain ergodic, which will ensure the existence of a unique stationary probability, which becomes the PageRank vector.
Example
Let Xn be the page the user visits in step n. Xn can be modeled by a Markov chain because the user's choice depends only on the current page.
Assuming that our "Internet" is made up of 7 pages, which are represented as the 7 nodes. Edges represent links between pages. Being on a page, a visitor randomly chooses a link to go to another page, so the probabilities of going from one page to the others are equal.

The transition matrix is:

We observe that there are 2 absorbing states: 4 and 7. The chain is not ergodic, it has 2 stationary probabilities and therefore it does not converge towards a single probability.
To avoid this situation, Page and Brin made an assumption:
Once the visitor lands on a "final" page (ie. no link to get out), he will go to the address bar and type in the address of a random site.
In terms of transition matrix, we will replace the column of the absorbing state by the vector:
![]()
The transition matrix T therefore becomes:

With this change, T is irreducible and aperiodic, hence ergodic. However, this is not always the case, taking the example with Math sites and Sport sites, we can obtain a transition matrix T:

It does not have absorbing states but it is not irreducible and therefore not ergodic. We need to make another assumption:
Supposing that the visitor is on a page, we say that with probability p he will choose one of the links on this page and with probability 1 − p he will go to the address bar and type the address of a random website.
The new transition matrix is therefore:
G = pT + (p − 1)K
with K the matrix of which each column is the vector:
![]()
The matrix G is called the Google matrix. G is ergodic. Google often uses p = 0.85.
Applying to our example, we get:

By solving Gπ = π, we find:
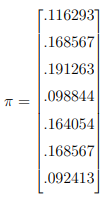
The ranking order in our example is therefore: 3,2,6,5,1,4,7. So if a searched word appears in pages 1,2,5, the order of the results is 2,5,1.
Break the system
If the PageRank value (which is also the stationary probability) of a page is p, the return time of this page is 1/p. So we can effectively increase the PageRank value by reducing the return time, which is possible if we create very short cycles, or ideally loops.
Concretely, for a page x, we delete all the links on it (ie. no exit), we create another page, y, with only 2 edges x → y and y → x. The PageRank value of page x increases because each time the visitor comes across this page, he cannot get out. As we discussed in part 3 (with the example of Maths and Sport), the PageRank algorithm can avoid the effect of this strategy by increasing the value of p, the probability that the visitor will go on the bar d address and type the address of a random site.
Another strategy is to create lots of pages that only have 1 edge to page x. This technique takes advantage of the probability p of restarting the walk. If we have a very large number of false pages, it is very likely that after starting again, we will come across page x, and therefore the PageRank value will increase. To avoid this situation, it is necessary to decrease the value of p.
Thanks to these 2 situations, we can clearly see that the choice of p is extremely important to avoid spam. If p is too high, spammers just have to create millions of bogus pages leading to their main pages. On the other hand, with a very small p, they can establish loops with their pages.
What we have discussed is only the basics of Google's search engine. The techniques have already evolved a lot to give the most relevant results. The question of computation is also very interesting. Since Google's true matrix is 8 billion x 8 billion in size, Gaussian's method of elimination is impractical. More powerful algorithms are used to find the eigenvectors, in particular the power method.
