Markov chains project: Computer Chess

Contents

The Markov chains project: Computer Chess, brings together notions of language theory and first-order discrete stochastic processes.

ETC: 15 hours (deadline - 5 classes)

2-3 students per team

Please take your time on both quality and contents

Associate professor and assistant professors will not answer questions about the project.

SCALE: 40 points

10 Points
15 Points
15 points

“Cameraman: Do you think a human being will ever beat a person at chess? John: Oh ... between a human being and a person? My money's on the computer. ”

Part 1: Readable and understandable data

" TO computer once beat me at chess, but it was no match for me at kick boxing. "

The challenge is tall, the annual global chess tournament to challenge the early computer scientists: to create a program capable of beating a human at chess. This is a first, and you have to show the world the potential of IT.

In order to familiarize yourself with the rules of chess, you watch in a loop the old tournaments of Mikhail Tal, Bobby Fisher and Anatoly Karpov as well as the promising debut of the young and formidable Garry Kasparov.

Possible moves (in terms of movement, not position) are recorded as symbols of the alphabet. A series of decision-making moves means that from a given favorable configuration, there is at least one strategy allowing to surely reach a favorable position of checkmate.

The computer will therefore build decision trees for favorable configurations (as in project 1). Take for example the following words for a favorable configuration A:

abbaaccad
baacdaadd
abaacdddd

In order to reduce the tree, we are going to use another technique than for subject 1. In the first step, you will assign in addition to the symbol, the number of times the arc has passed. Initially this number is equal to 1 for each arc.

The second step consists in calculating the coefficient of compatibility between two states. In our example we will merge two states if they are 100% compatible. Two states are 100% compatible if they have the same predecessor and successor symbols. For example on the prefixes abba and baab, the binomial ab or ba are 100% compatible. During the merger, it is also necessary to merge the number of passages through the arcs (so here we sum 1 + 1).

The third step is to merge compatible 50% states, that is to say with only the same successors or only the same predecessors. It is therefore possible to converge the final states into a single final state, since all the final states have the same successors (here the empty set).

The fourth and last step is used to manufacture the Markov chain in associated discrete time. For each state, the probability of the entry (resp. Exit) arcs is equal to the number of passages of this arc divided by the sum of the numbers of entry (or exit, this number is the same).

Rating

Step 1 (2 points)
2nd step (3 points)
Step 3 - do not converge on all the possible cases, at least two of which the final state (3 points)
Step 4 (2 points)

Part 2: Behavior study

" Beuscher: Is there any possibility that this is uh… some kind of uh… very advanced… I mean, we just gave up a queen to get his queen and now we're basically just… um… ”

Now that you have stochastic automata (a delicious mix of automaton and markov chain), it is time to study their behavior, that is, the study of the associated Markov chain. Remember to carefully analyze the final states (checkmate).

Study the behavior of the following two discrete-time Markov chains:

State 6 is a final state.

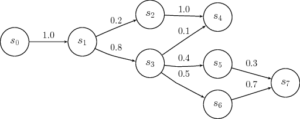
The absorbing states are the “checkmate” configurations. The state s0 is the initial state, the initial vector therefore begins only with this state.

Rating

Channel 1 (7 points)
Channel 2 (8 points)

Part 3: Automaton reduction and prediction

“Chess is the struggle against the error.” - Johannes zukertort

Now that your machine learning system is up and running, it's time to think about the technical part. Your computer has two Cores and thus it is possible to do parallel computing. The Bus problem then arises, do you need one Bus or two Buses to route the information to the processors? Knowing that information always arrives according to a Poisson process of rate λ and that they are served with a Poisson process of similar rate, calculate the stationary distribution, the occupation of the processors, the number of messages lost as well as the average waiting time before being served for both setups.

Rating

Modeling of the two configurations (5 points)
Analysis of the first configuration (5 points)
Analysis of the second configuration (5 points)