Invariant law and asymptotic behavior

Invariant law and asymptotic behavior

We seek to understand the asymptotic behavior of a homogeneous Markov chain. That is to say the limit of the transition probabilities Q^not(i, j) when n becomes very large (the invariant law).

Idea

We seek to answer the following question: "What is the probability that after n
not here markov chain be in a given state? ". Take the following transition matrix P:

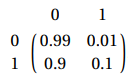
Suppose none of the machines are down on the first day. Then we have as initial vector (1, 0), to calculate the following distribution we multiply the initial vector by P, etc. Which gives the following results:

This means that after 10 iteration, if we consider that we are starting from state 0, we have 99% to be in state 0 and 1% in state 1. This can also be interpreted as follows: on a starting population, considering the initial distribution by vector (1.0), then 99% of the population will be in state 0 and 1% in state 1.

We notice that the fourth and the tenth iteration have similar results (here identical to 4 significant digits). We then speak of a law of convergence, and this law does not depend on the distribution at the origin.

Periodicity

Let us take the example of the following matrix P = {0, 1; 1, 0}. We note that P² = Id which implies the following relation: ∀n∈Ν, P^{2n + 1}= P.

Such a chain does not converge, we say that it is 2-periodic or of period 2.

Before calculating the invariant law of a Markov chain, it is necessary to verify that the latter is irreducible and aperiodic (also called ergodic).

A chain is therefore ergodic if any state can be reached from any other state and for a power P^k all elements are strictly positive. It is therefore possible to go from one state to another in at most k stages, independently of the starting and ending points. An ergodic chain has an invariant law (be careful, it is also possible to calculate the stationary distribution of the other chains, the interpretation is not the same).

Invariant law

One says that a probability measure π is invariant or stationary if for a transition matrix P we have πP = π. Note that since π is a measure then the sum of these terms is equal to 1.

Let (Xn) defining a homogeneous Markov chain with P an irreducible aperiodic transition matrix having an invariant measure π. Then :

• P (Xn = x) → π (x) when n → ∞ for all x
• p^not(x, y) → π (y) when n → ∞ for all x, y

The speed of convergence towards the stationary law is of the order of | ζ |^not where ζ is the eigenvalue of P different from 1 and of greater modulus (which is strictly less than 1).

If the chain is ergodic (irreducible and aperiodic) then all states are reachable from any other state. Such a chain has an invariant law.

Exact calculation of the measurement

Let us take the definition µP = µ knowing that µ is stochastic (and yes I changed the name of the initial distribution!). This gives the following linear system:

A measure µ on E is invariant (for P) if µ = µP, i.e. for all y ∈ E

We speak of an invariant law if in addition µ is a probability (µ (E) = 1). We also say invariant / stationary law / probability.

Given the relation µ_{n + 1} = µ_notP, we see immediately that, if µ is an invariant law and X₀ ∼ µ, then X_not ∼ µ for all n. We also notice that µ does not depend on the initial distribution vector.

Take for example a three-state Markov chain, whose transition matrix is as follows:

We notice immediately that the matrix forms an irreducible and aperiodic chain, since all the states communicate and that p_ii > 0. We seek to solve the system µP = µ with for solution µ * = (p, q, r) such that p + q + r = 1 and 0 <p,q,r <1 ce qui donne les équations suivantes :

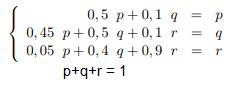
We find as a solution the vector µ * = (2/53, 10/53, 41/53).

Exact calculation of the measurement (non-ergodic case)

Consider the following Markov chain

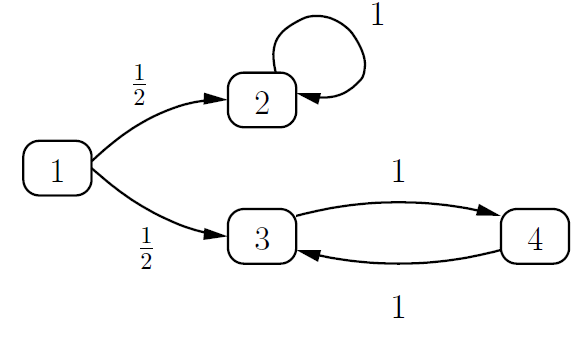
We find that state 1 forms a transitional class, state 2 forms an absorbing class and states 3, 4 form a recurrent class. Let us make the analysis of the asymptotic behavior by not taking account of its nonergotic character (no guarantee of convergence).

Let's solve the following system:

The system does not allow a single solution. Let α be between 0 and 1, then we find a solution by admitting that α is solution of π2:

We notice in the class {3,4} that the probabilities are equal on a frequency of 2k, we deduce that the class is periodic over a period of 2 (which we could have calculated by power of the matrix). Class {2} is absorbing, there is no period. The class {1} is transient, which is why there is no longer a population after a time k.

In the case of a non-periodic chain, it is possible to deduce from the asymptotic behavior the classes of the states as well as the periodicities of the classes and of the chain.