Contents
ToggleRecurrence and transience criteria
We will study a second classification of states depending on the type of behavior of the chain (the criteria of recurrence and transience).
Let x be a state of the chain, we denote the time to reach x, denoted by Tx, the first instant when x is visited after departure. by convention, the reach time is infinite if we never reach x. The formula is as follows (we will use the classical notations for the probabilities):

If the chain starts from state x, we use the term return time.
A state x is said to be recurrent if:![]()
State x is said to be transient or transient otherwise, i.e. when:
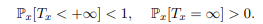
A state is recurrent if we are sure to return to it, it is transient if there is a non-zero probability of never coming back to it, and therefore of leaving it definitively.
An equivalence class is said to be recurrent, respectively transient, if one of its vertices is recurrent, resp. transient.
Let x be any state belonging to the recurrence class C. Suppose
that there exists y ∉ C such that x → y and let us show that we have a contradiction. Note first that y does not lead to any vertex of C, because otherwise we would have y → x and therefore x ↔ y and y ∈ C. Moreover, we have:
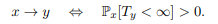
However, the probability of not going back to x is bounded inferiorly by the probability of going to y in finite time (since y does not lead to any state of C). So, we have the following relation:
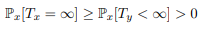
Which is a contradiction with recurrent x. We see that a recurring class is closed, but the converse is false in general, it is still verified if this class has a finite cardinality.
