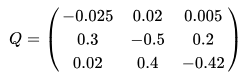Continuous-time Markov chains

Difficulty

Average 50%

Contents

In the case of discrete time, we observe the states on instantaneous and immutable moments. Within the framework of Markov chains in continuous time, the observations are continuous, that is to say without temporal interruption.

Continuous time

Let M + 1 be mutually exclusive states. The analysis starts at time 0 and time runs continuously, we call X (t) the state of the system at time t. The state change points t_i are random points in time (they are not necessarily whole). It is impossible to have two state changes at the same time.

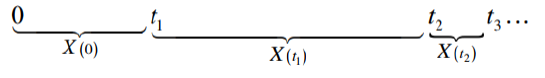
Consider three consecutive points in time where there has been a change of states r in the past, s at the present time and s + t in the future. X (s) = i and X (r) = l. A continuous-time stochastic process with the Markov property if:

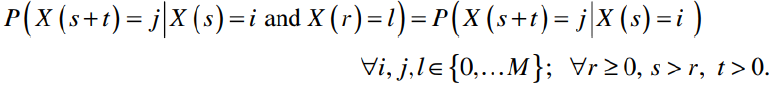
The transition probabilities are stationary since they are independent of s. We denote by p_ij(t) = P (X (t) = j, X (0) = i) the continuous-time transition probability function.

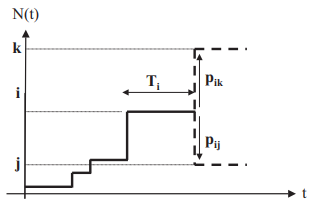
Denote by T_i a random variable denoting the time spent in state i before moving to another state, i∈ {0,…, M}. Suppose the process enters state i at time t '= s. Then for a duration t> 0, T_i > t ⇔ X (t '= i), ∀t'∈ [s, s + t].

The stationarity property of the transition probabilities results in: P (T_i > s + t, T_i > s) = P (T_i > t). The distribution of the time remaining until the next output of i by the process is the same regardless of the time already spent in state i. The variable T_i is memoryless. The only continuous random variable distribution having this property is the exponential distribution.

The exponential distribution T_i has only one parameter q_i and its mean (mathematical expectation) is R [T_i ] = 1 / q_i. This result allows us to describe a markov chain in continuous time in an equivalent way as follows:

The random variable T_i has an exponential distribution of parameter λ
when the process leaves state i, it goes to state j with a probability p_ijsuch as (similar to a discrete-time Markov chain):
the next state visited after i is independent of the time spent in state i.
The continuous-time Markov chain has the same Class and Irreducibility properties as the discrete-time chains.

Here are some properties of the exponential law:

Duration model

Thus, if we consider μ_i the parameter of the exponential random variable associated with state i, we can represent the continuous-time Markov chain as follows:

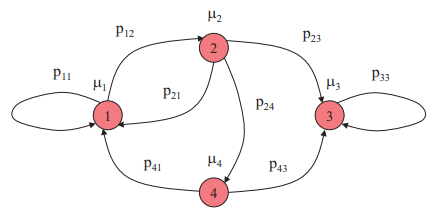
We can clearly see the included discrete-time Markov chain, hence the possibility of carrying out a study of the discrete model. Note that there is no notion of periodicity in this context.

If we consider that we move from state i to state j after a time T_ij and that we consider this time as an exponential random variable of rate μ_ij, then it is possible to write the Markov chain in continuous time under a duration model:

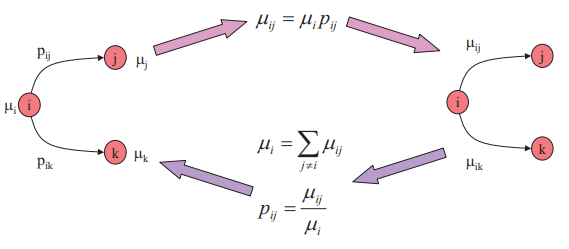
Be careful, there is a big change between the stochastic side of the movement from one state to another and the continuous side in time. It is important to understand that the transition matrix of a continuous time Markov chain is always a duration model.

The transition matrix of a duration model has the following properties:

This matrix is called the infinitesimal generator.

Thus, from the graph following discrete Markov equation (the exponential law is the same in the three states):

It is possible to obtain the following time model: