Contenus

Programmation par contraintes

La programmation par contraintes permet de résoudre des problèmes décisionnels. Un problème d’optimisation se résout successivement après plusieurs problèmes de décision. Par exemple pour déterminer un plus court chemin, nous chercherons a trouver un chemin de moins de 100 (possible), puis moins de 50 (impossible), puis moins de 75, etc. jusqu’à trouver la solution optimale. La PPC a un champ d’action plus large que les méthodes exactes ou les méta-heuristiques.

Définition

La PPC résout un problème de satisfaction de contraintes (CSP).

Ce dernier est défini par un triplet <X,D,C> avec X l’ensemble de variables, D l’ensemble de domaines et C l’ensemble de contraintes. Le Domaine D_i est l’ensemble des valeurs possibles pour la variable X_i. Chaque contraintes C_j se définit par son arité (le nombre de variable sur lesquelles elle porte), la liste de ces variables et l’ensemble des tuples qui la satisfont.

Prenons un exemple de triplet :

variables : A, B, C, D
domaines :
- D_A = {1,4,5,8}
- D_B = {2,3,5,7,9}
- D_C = {4,8,9}
- D_D = {1,4,5,7,9}
contraintes :
- C₁(A,C) : {(1,7); (1,9); (5,9); (8,9)}
- C₂(A,D) : (1,1);(1,5);(5,5);(5,9);(8,9)}
- C₃(C,D) : {(4,1);(8,1);(9,7)}
- C₄(B,D) : {(2,7);(2,9);(5,8);(7,9);(9,9)}

Il est possible de coder les contraintes en extension, par un ensemble de tuples, ou en intention, en utilisant des opérateurs dont la sémantique est connue. Une instanciation est une affectation complète de valeurs aux variables, par exemple {<A,1>,<B,7>,<C,4>,<D,9>}. L’instanciation est une solution valide si les valeurs données aux variables dont telles que toutes les contraintes sont vérifiées.

On parle d’instanciation partielle ou totale (si elle prend toutes les variables ou non), et inconsistante ou consistante (si elle valide les contraintes ou non). Une solution valide est donc une instanciation totale et consistante.

Résolution naïve : Generate & Test

On génère toutes les affectations possibles. Puis on vérifie si elles sont consistantes, dès qu’une affectation est consistante nous avons une solution valide.

Si on a un problème à n variables, chacune ne peut prendre que deux valeurs, le processeur fait 1000000000 calcul à la seconde. Pour 30 variables, la résolution prendre au plus 1s, pour 50 variables, on passe à 11 jours; pour 70 variables il faut attendre 317 siècles.

Résolution par backtrack

On génère l’arbre des affectations puis on le parcours en profondeur. Si une affectation partielle (durant le parcours) est inconsistante, alors on coupe le sous-arbre correspondant.

Cela s’apparente à du Branch&Cut.

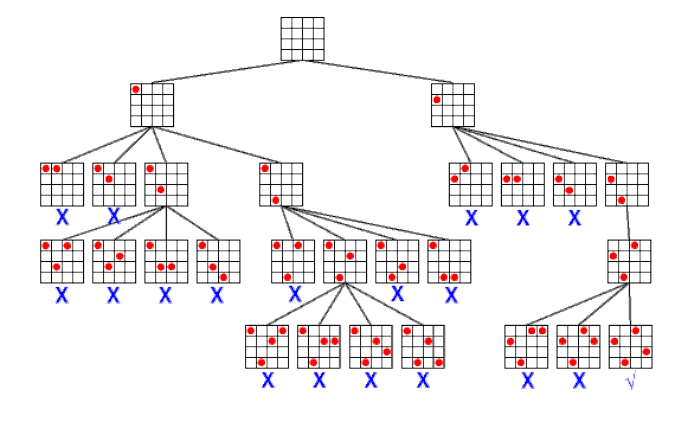
Cette méthode ne génère pas l’arbre des possibilités en entier contrairement à la méthode naïve. Par contre toutes les contraintes sont testées à chaque affectation partielle et le temps de convergence dépend aussi de l’ordre des variables.

Résolution par propagation de contraintes

Cette méthode consiste à propager les contraintes dans le domaine des variables.

Par exemple prenons x entre 0 et 10 et y entre 3 et 9; alors avec la contrainte x>y nous pouvons restreindre le domaine de X entre 4 et 10.

programmation par contraintes propagation

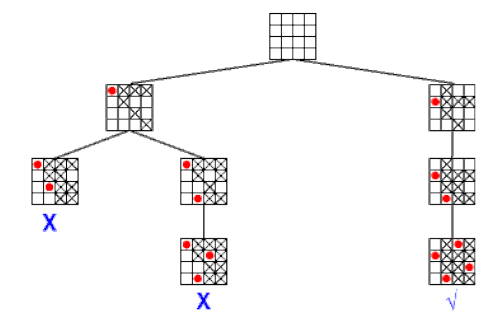
Il existe trois cas où l’on propage l’information :

quand un domaine est réduit
quand une des bornes du domaine est changée
quand un domaine est un singleton.

Il est alors possible de propager l’information une fois (noeud-consistance), deux fois (arc-consistance) ou plus.

Dans le noeud-consistance, pour chaque variable X_i non affectée dans A, on enlève de D_Xi toute valeur v telle que l’affectation A ∪{(X_i,v)} est inconsistante. On propage les valeurs autorisées en profondeur.

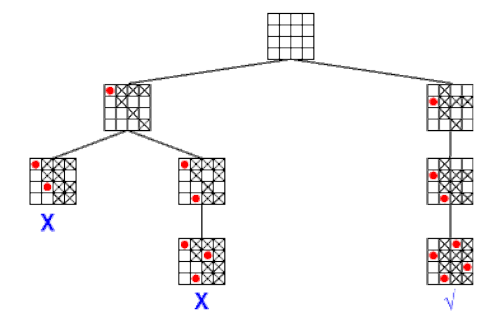
Dans l’arc-consistance, pour chaque variable X_i non affecté dans A, on enlève de D_Xi toute valeur v telle qu’il existe une variable X_j non affectée pour laquelle, pour toute valeur w de D_Xj, l’affectation A ∪{(X_i,v);(X_j,w)} soit inconsistante. On propage les valeurs autorisées en profondeur.

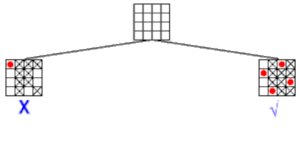
Plus le tuple de comparaison est grand, plus le temps de calcul pour définir le domaine valide des variables est grand. L’arc-consistance se révèle moins efficace que le noeud-consistance si les domaines sont grands.