Contenus
ToggleMéthode de coupes planes (cutting-plane)
La méthode de coupes planes (cutting-plane) a été développée par Schrijver, elle est destinée à résoudre des problèmes d’optimisation combinatoire (POC) qui se formulent sous la forme d’un programme linéaire (PL) :
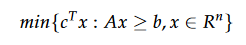
Dans le cas, où le POC est de grande taille pour le représenter explicitement en mémoire ou pour qu’il tient dans un solveur de programmation linéaire, on utilise une technique qui consiste à enlever une partie de ces contraintes et de résoudre le problème relaxé (POCR). La solution optimale de (PL) est contenue dans l’ensemble de solutions réalisables de cette relaxation. Pour un problème de minimisation la solution optimale du problème (POCR) est inférieure ou égale à la solution optimale donnée par (POC)
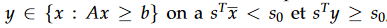
Cette méthode consiste à résoudre un problème relaxé, et à ajouter itérativement des contraintes du problème initial. On définit une contrainte pour le problème de minimisation par le couple(s,s0) où s est dans Rn et s0 dans R, cette contrainte est dite violée par la solution courante x(barre) si pour tout :
On appelle alors ces contraintes des coupes planes. On arrête l’algorithme lorsqu’il n’y a plus de contraintes violées par la solution courante, on obtient ainsi une solution optimale pour le problème initial.
La méthode des coupes planes est peu performante mais sa performance est améliorée lorsqu’elle est combinée avec la méthode Branch and Bound.
