Contenus
ToggleCutting-plane method
The cutting-plane method was developed by Schrijver, it is intended to solve combinatorial optimization (POC) problems which are formulated in the form of a linear program (PL):
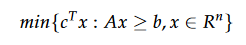
In the case, where the POC is of large size to represent it explicitly in memory or so that it fits in a solver of linear programming, we use a technique which consists in removing part of these constraints and solving the relaxed problem (POCR). The optimal solution of (PL) is contained in the set of feasible solutions of this relaxation. For a problem of minimization the optimal solution of the problem (POCR) is less than or equal to the optimal solution given by (POC)
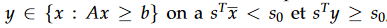
This method consists in solving a relaxed problem, and in iteratively adding constraints to the initial problem. We define a constraint for the problem of minimization by the couple (s, s0) where s is in Rnot and s0 in R, this constraint is said to be violated by the current solution x (bar) if for all:
These constraints are then called plane sections. One stops the algorithm when there are no more constraints violated by the current solution, one thus obtains an optimal solution for the initial problem.
The plane cuts method is not very efficient but its performance is improved when it is combined with the method Branch and Bound.
