Difficulté
Facile
25%
Contenus
ToggleProcessus de Poisson
Un processus de Poisson de paramètre λ est un processus stochastiques N(t) tel que N(O)=0, N(t) est incrémenté de +1 après un temps T distribué suivant une loi exponentielle de paramètre λ. On parle d’arrivées de Poisson si le temps entre deux arrivées est exponentiel.
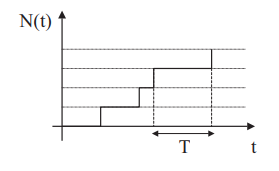
Prenons pour état la valeur de N(t), alors la chaîne de Markov en temps continu associé au processus de Poisson λ est :

Il est possible de connaitre la probabilité pour que N soit au nombre k au temps t par la formule :

N(t) est distribué suivant une loi de Poisson de paramètre λt.
Les processus de Poisson s’associe et se décompose de la façon suivant :
- La superposition de n processus de Poisson est un processus de Poisson ayant pour paramètre la somme des n paramètres
- Un processus de Poisson qui se décompose en n processus avec des probabilités pi. Ces n processus sont alors des processus de Poisson de taux respectifs λpi

