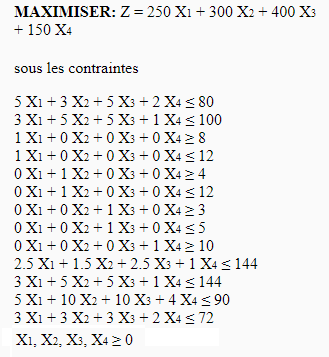Contenus
ToggleExercices Corrigés sur la modélisation linéaire à partir d'énoncé
Ci-dessus des exercices corrigés de modélisation linéaire.

Exercice 1
Une entreprise fabrique deux produits A et B, en utilisant une machine m et deux matières premières p et q. On dispose chaque jour de 8 heures de m, de 10 kg de p et de 36 kg de q. On suppose que :
- la production d’une unité de A nécessite 2 kg de p et 9 kg de q, et utilise la machine m durant 1 heure ;
- la production d’une unité de B nécessite 2 kg de p et 4 kg de q, et utilise la machine m durant 2 heure ;
- les profits réalisés sont de 50€ par unité de A et 60€ par unité de B
L’objectif que poursuit l’entreprise est de maximiser le profit qu’elle pourra tirer, par jour, de ces 2 produits en utilisant au mieux ses ressources.
- Ecrire un tableau pour récapituler les informations
- Définir les variables
- Définir les contraintes
- Définir la fonction objectif
- Le tableau suivant résume les données afférentes à ce problème de production :
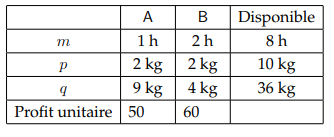
2. Ici deux données sont inconnus : le quantité de produit A à produire et la quantité de produit B à produire. Nommons les respectivement x1 et x2. Nous avons deux variables dans notre problèmes de décision.
3. Il faut comprendre comment les variables de décision sont contraintes. Pour cela, il faut se servir des données dans le cahier des charges.
- Contrainte de la machine m (première ligne) : Le temps d’utilisation de la machine m pour fabriquer les produits A et B ne peut excéder les 8 heures disponibles : m≤8.
- La machine produit une unité de A en 1h
- La machine produit une unité de B en 2h
- Reformulons la contrainte par : la quantité de A et B produite ne dépasse pas 8h
- x1 + 2*x2 ≤8
- Contrainte de la matière p : La quantité de matière p ne peut pas excéder 10kg
- Une unité de A consomme 2kg de p
- Une unité de B consomme 2kg de p
- Formulation de la contrainte : la quantité de produit utilisée par A et B ne dépasse pas 10kg
- 2* x1 + 2 *x2 ≤ 10
- Contrainte de la matière q : de même nous en concluons que la quantité de produit utilisée par A (9kg par unité) et par B (4kg par unité) ne dépasse pas 36kg
- 9 * x1 + 4 *x2 ≤ 36
- Contrainte de positivité : il est a noté que le texte ne donne pas d’information direct sur les variables de décision. Cependant, il est logique que ces dernières soient positive ou nul, il parait improbable de produire -1 unité de A.
- x1 , x2 ≥ 0
4. La fonction objectif est comme son nom l’indique l’objectif de l’industriel : maximiser son profit. Nous savons que la vente d’une unité de A rapporte 50€ et que la vente d’une unité de B rapporte 60€. Posons z le profit total, alors le fonction objectif est max z = 50 * x1 + 60 *x2 .
Le modèle mathématique linéaire, noté (P), se résume ainsi :
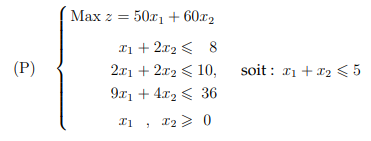
Exercice 2
Une entreprise de fabrication de châssis envisage la production de deux nouveaux modèles au moyen des capacités de ses trois ateliers. Il s’agit respectivement d’un châssis en aluminium et d’un châssis en bois.
Le premier produit nécessite le passage dans le premier atelier pour fabriquer le cadre en aluminium et dans le troisième atelier où le verre est monté sur le châssis. Tandis que le second produit nécessite le passage dans le deuxième atelier pour fabriquer le cadre en bois et dans le troisième atelier où le verre est monté sur le châssis. Les profits unitaires, les temps de fabrication de chacun des produits dans chacun des ateliers ainsi que les capacités hebdomadaires de ces ateliers sont donnés au tableau suivant :

Formuler le problème linéaire.
Les contraintes sont sur les trois premières lignes tandis que la fonction objectif est sur la dernière ligne. Ce qui donne : X1 pour le produit 1 et X2 pour le produit 2
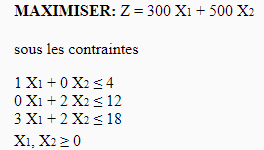
Exercice 3
Un producteur d’électricité souhaite que ces deux centrales nucléaires P et Q fournissent une quantité d’énergie aux villes A, B et C. Les quantités d’énergie minimales à satisfaire sont de 16 pour A, 12 pour B et 18 pour C.
Quand un réacteur de P produit, il envoie 2 unités à A, 1 unité à B et 1 unité à C ; et coûte 20€ par jour. Quand une réacteur de Q produit, il envoie 1 unité à A, 1 unité à B et 3 unités à C ; et il coûte 40 €. Le producteur cherche la combinaison la moins coûteuse de réacteurs de P et Q qui respectera l’exigence de consommation minimale pour les villes A, B, C. Les données sont récapitulé dans le tableau suivant :
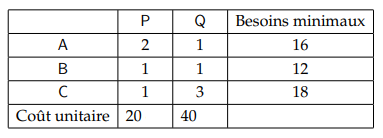
Formuler le problème linéaire.
Les contraintes sont sur les trois premières lignes tandis que la fonction objectif est sur la dernière ligne. Ce qui donne : X1 pour le producteur P, X2 pour le producteur Q
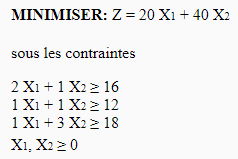
Exercice 4
La suite d’exercices ci-après ne sont pas indépendants, les contraintes s’accumulent ou changent d’une partie à l’autre.
Une usine automobile reçoit chaque semaine 100 tonnes d’aluminium et 80 tonnes d’acier. L’usine produit trois types de véhicule de chantiers : Transport, Gros oeuvre, Grue; vendu respectivement 250k€, 300k€ et 400k€.
La production de Transport demande 5 tonnes d’aluminium et 3 tonnes d’acier; le Gros Oeuvre a besoin de 3 tonnes d’aluminium et 5 tonnes d’acier; la Grue requiert 5 tonnes de chaque. Formuler le problème linéaire afin de maximiser les gains de l’usine.
Le programme linéaire est le suivant : X1 pour le Transport, X2 pour le Gros oeuvre et X3 pour la Grue
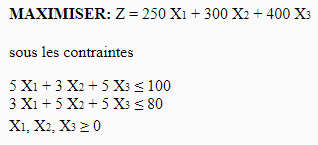
Exercice 5
L’équipe Marketing prévient l’usine que la production de véhicule ne suit pas la demande des clients. Après une étude des statistiques de ventes sur la dernière année, les analystes financiers en on déduit les données suivantes : il se vend en moyenne 10 Transport par semaine, avec un écart type de 2 véhicules (confiance de 99%); il se vend en moyenne 8 Gros Oeuvre par semaine, avec un écart type de 4 véhicules (confiance de 99%); il se vend en moyenne 4 Grues par semaine avec un écart type de 1 Grue (confiance de 99%). Formuler le problème pour maximiser les gains de l’usine.
Voici le programme linéaire avec les nouvelles contraintes :
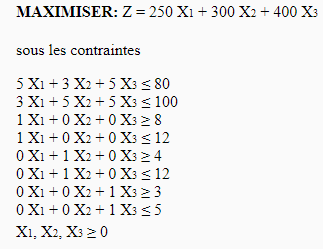
Exercice 6
Grosse erreur de votre part, en souhaitant toujours maximiser les gains, vous n’avez pas pris en compte le temps de travail et le confort des ouvriers ! Ces derniers réclament à juste titre que la production réponde à leur condition de travail. Ces derniers sont réparti en trois ateliers.
La fonderie possède deux cuves en fonctionnement 24/24h et 6/7j, 1 tonne d’aluminium prend 30min à fondre et 1 tonne d’acier prend 1h à fondre (chaque cuve est configurée pour un des deux métaux). La chaîne de montage est ouverte 15/24h et 6/7j, un Transport est monté en 5h, le Gros Oeuvre en 10h et une grue en 10h. L’atelier de finition est ouvert 12/24h et 6/7j, la finition prend 3h quelque soit le véhicule. Formuler le problème pour maximiser les gains de l’usine.
Le programme linéaire avec les nouvelles contraintes est :

Exercice 7
L’équipe de développement de l’usine a créé un nouveau véhicule révolutionnaire ! Ce véhicule Test a besoin de seulement 2 tonnes d’aluminium et 1 tonne d’acier pour un prix de vente estimé à 150k€. L’étude du marché montre qu’il peut s’en vendre au minimum 10 unités par semaine. Ce véhicule est monté en 4h et la finition ne dure que 2h. Formuler le problème pour maximiser les gains de l’usine.
Le programme linéaire après ajout d’une nouvelle variable X4