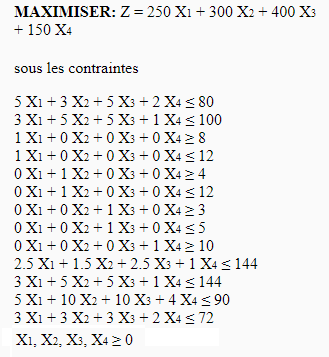Contents
ToggleCorrected exercises on linear modeling from statements
Above corrected exercises of linear modeling.

Exercise 1
A company manufactures two products A and B, using a machine m and two raw materials p and q. We have 8 hours of m, 10 kg of p and 36 kg of q every day. We suppose that :
- the production of a unit of A requires 2 kg of p and 9 kg of q, and uses the machine m for 1 hour;
- the production of a unit of B requires 2 kg of p and 4 kg of q, and uses the machine m for 2 hours;
- the profits made are € 50 per unit of A and € 60 per unit of B
The company's objective is to maximize the profit it will be able to derive, per day, from these 2 products by making the best use of its resources.
- Write a table to summarize the information
- Define the variables
- Define the constraints
- Define the objective function
- The following table summarizes the data pertaining to this production problem:
2. Here two data are unknown: the quantity of product A to produce and the quantity of product B to produce. Let us name them respectively x1 and x2. We have two variables in our decision problems.
3. Understand how the decision variables are constrained. For this, it is necessary to use the data in the specifications.
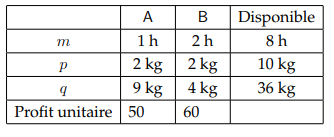
- Constraint of the machine m (first line): The time of use of the machine m to manufacture products A and B cannot exceed the 8 hours available: m≤8.
- The machine produces a unit of A in 1 hour
- The machine produces a unit of B in 2 hours
- Let us reformulate the constraint by: the quantity of A and B produced does not exceed 8h
- x1 + 2 * x2 ≤8
- Constraint of material p: The quantity of material p cannot exceed 10kg
- A unit of A consumes 2kg of p
- A unit of B consumes 2kg of p
- Formulation of the constraint: the quantity of product used by A and B does not exceed 10kg
- 2 * x1 + 2 * x2 ≤ 10
- Constraint of the material q: similarly we conclude that the quantity of product used by A (9kg per unit) and by B (4kg per unit) does not exceed 36kg
- 9 * x1 + 4 * x2 ≤ 36
- Constraint of positivity: it is noted that the text does not give direct information on the decision variables. However, it is logical that these are positive or zero, it seems unlikely to produce -1 unit of A.
- x1 , x2 ≥ 0
4. The objective function is, as its name suggests, the industrialist's objective: to maximize his profit. We know that selling a unit of A earns $ 50 and selling a unit of B earns $ 60. Let z be the total profit, then the objective function is max z = 50 * x1 + 60 * x2 .
the mathematical model linear, noted (P), can be summarized as follows:
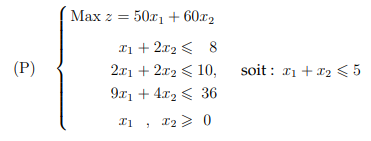
Exercise 2
A chassis manufacturing company plans to produce two new models using the capabilities of its three workshops. These are respectively an aluminum frame and a wooden frame.
The first product requires going to the first workshop to make the aluminum frame and to the third workshop where the glass is mounted on the frame. While the second product requires the passage in the second workshop to manufacture the wooden frame and in the third workshop where the glass is mounted on the frame. The unit profits, the manufacturing times of each of the products in each of the workshops as well as the weekly capacities of these workshops are given in the following table:

Formulate the linear problem.
The constraints are on the first three lines while the objective function is on the last line. Which gives: X1 for product 1 and X2 for product 2
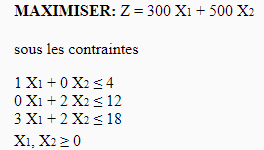
Exercise 3
An electricity producer wants these two nuclear power plants P and Q to supply a quantity of energy to cities A, B and C. The minimum quantities of energy to be satisfied are 16 for A, 12 for B and 18 for C.
When a reactor of P produces, it sends 2 units to A, 1 unit to B and 1 unit to C; and costs 20 € per day. When a reactor of Q produces, it sends 1 unit to A, 1 unit to B and 3 units to C; and it costs 40 €. The producer is looking for the cheapest combination of P and Q reactors that will meet the minimum consumption requirement for cities A, B, C. The data is summarized in the following table:
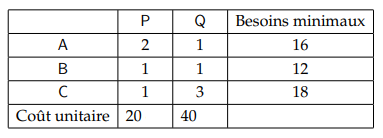
Formulate the linear problem.
The constraints are on the first three lines while the objective function is on the last line. Which gives: X1 for producer P, X2 for producer Q
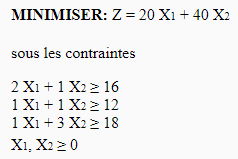
Exercise 4
The following exercises are not independent, the constraints accumulate or change from one part to another.
A car factory receives 100 tonnes of aluminum and 80 tonnes of steel every week. The factory produces three types of construction vehicle: Transport, Structural work, Crane; sold respectively 250k €, 300k € and 400k €.
The production of Transport requires 5 tonnes of aluminum and 3 tonnes of steel; the Structural Work needs 3 tonnes of aluminum and 5 tonnes of steel; the Crane requires 5 tons of each. Formulate the linear problem in order to maximize the gains of the plant.
the linear program is as follows: X1 for the Transport, X2 for the Shell and X3 for the Crane
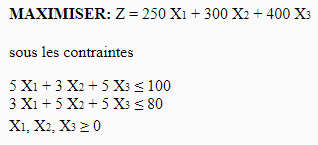
Exercise 5
The Marketing team warns the plant that vehicle production is not keeping up with customer demand. After a study of sales statistics for the last year, financial analysts deduced the following data: an average of 10 Transport per week is sold, with a standard deviation of 2 vehicles (confidence of 99%); an average of 8 Big Work per week is sold, with a standard deviation of 4 vehicles (confidence of 99%); an average of 4 Cranes is sold per week with a standard deviation of 1 Crane (confidence of 99%). Formulate the problem to maximize the gains of the plant.
Here is the linear program with the new constraints:
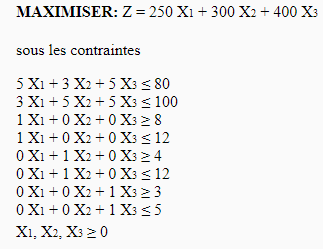
Exercise 6
Big mistake on your part, by always wishing to maximize profits, you did not take into account the working time and the comfort of the workers! The latter rightly claim that production meets their working conditions. These are divided into three workshops.
The foundry has two tanks in operation 24/7, 1 tonne of aluminum takes 30 minutes to melt and 1 tonne of steel takes 1 hour to melt (each tank is configured for one of the two metals). The assembly line is open 15 / 24h and 6 / 7d, a Transport is assembled in 5h, the Big Work in 10h and a crane in 10h. The finishing workshop is open 12 hours a day, 6 days a week, finishing takes 3 hours whatever the vehicle. Formulate the problem to maximize the gains of the plant.
The linear program with the new constraints is:

Exercise 7
The factory development team has created a revolutionary new vehicle! This Test vehicle only needs 2 tons of aluminum and 1 ton of steel for an estimated selling price of 150k €. Market research shows that it can sell at least 10 units per week. This vehicle is assembled in 4 hours and the finish only lasts 2 hours. Formulate the problem to maximize the gains of the plant.
The linear program after adding a new variable X4