Apprentissage de la quantification vectorielle

Algorithme d’apprentissage de quantification vectorielle

L’apprentissage de quantification vectorielle est lié à la carte auto-organisatrice qui est à son tour inspirée par les capacités d’auto-organisation des neurones dans le cortex visuel.

L’objectif de traitement de l’information de l’algorithme d’apprentissage de quantification vectorielle est de préparer un ensemble de vecteurs codebooks (ou prototype) dans le domaine des échantillons de données d’entrée observés et d’utiliser ces vecteurs pour classer des exemples non traités. Un pool de vecteurs initialement aléatoire est préparé qui est ensuite exposé à des échantillons d’apprentissage.

Une stratégie le gagnant prend tout est utilisée où un ou plusieurs des vecteurs les plus similaires à un modèle d’entrée donné sont sélectionnés et ajustés pour être plus proches du vecteur d’entrée, et dans certains cas, plus éloignés du gagnant pour les finalistes. La répétition de ce processus entraîne la distribution de vecteurs codebooks dans l’espace d’entrée qui se rapprochent de la distribution sous-jacente des échantillons de l’ensemble de données de test.

L’algorithme d’apprentissage de quantification vectorielle est une technique de traitement du signal où les fonctions de densité sont approximées avec des vecteurs prototypes pour des applications telles que la compression. L’apprentissage de la quantification vectorielle est similaire en principe, bien que les vecteurs prototypes soient appris par une méthode supervisée le gagnant prend tout.

L’algorithme suivant fournit un pseudocode pour préparer des vecteurs codebooks à l’aide de la méthode d’apprentissage de quantification vectorielle. Les vecteurs codebooks sont initialisés à de petites valeurs à virgule flottante ou échantillonnés à partir d’un ensemble de données disponible. L’unité de meilleure correspondance (BMU) est le vecteur codebooks du pool qui a la distance minimale à un vecteur d’entrée. Une mesure de distance entre les motifs d’entrée doit être définie. Pour les vecteurs à valeur réelle, il s’agit généralement de la distance euclidienne:

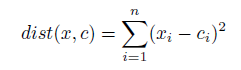
où n est le nombre d’attributs, x est le vecteur d’entrée et c est un vecteur codebooks donné.

La quantification des vecteurs d’apprentissage a été conçue pour les problèmes de classification qui contiennent des ensembles de données existants qui peuvent être utilisés pour superviser l’apprentissage par le système. L’algorithme ne prend pas en charge les problèmes de régression. LVQ est non paramétrique, ce qui signifie qu’il ne repose pas sur des hypothèses concernant la structure de la fonction qu’il est en train d’approcher. Les valeurs réelles dans les vecteurs d’entrée doivent être normalisées de telle sorte que x soit dans [0; 1].

La distance euclidienne est couramment utilisée pour mesurer la distance entre des vecteurs à valeur réelle, bien que d’autres mesures de distance puissent être utilisées (comme le produit scalaire), et des mesures de distance spécifiques aux données peuvent être requises pour les attributs non scalaires. Il doit y avoir des itérations d’entraînement suffisantes pour exposer toutes les données d’entraînement au modèle plusieurs fois. Le taux d’apprentissage est typiquement linéairement décroissant au cours de la période d’apprentissage en partant d’une valeur initiale proche de zéro. Plus la distribution des classes est complexe, plus il faudra de vecteurs codebooks, certains problèmes peuvent en nécessiter des milliers.

Plusieurs passes de l’algorithme de formation LVQ sont suggérées pour une utilisation plus robuste, où la première passe a un taux d’apprentissage élevé pour préparer les vecteurs codebooks et la seconde passe a un faible taux d’apprentissage et s’exécute pendant une longue période (peut-être 10 fois plus d’itérations).