Contenus
ToggleMéthodes de descente
Comme le nom explicite l’indique, les méthodes de descente, ou recherche locale, consiste à « glisser » le long de la fonction objectif jusqu’à trouver un optimum local, c’est-à-dire où la descente n’est plus possible. Il existe plusieurs sortes de méthode de descente qui nous décrirons ici.
Descente simple
À partir d’une solution initiale, l’algorithme de descente simple choisit une solution voisine meilleure que la solution courante, jusqu’à ne pas pouvoir effectuer un tel choix.
L’algorithme est le suivant :
S_O
faire
S(i+1) = voisin(Si)
si f(S(i+1)) < f(Si)
accepter S(i+1)
fin si
tant que f(S(i+1)) < f(Si), qqsoit S(i+1) = voisin(Si)
retourne Rn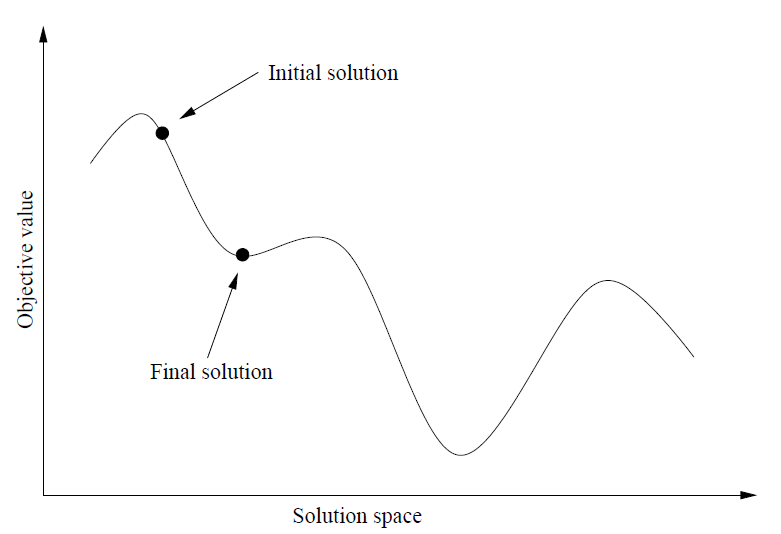
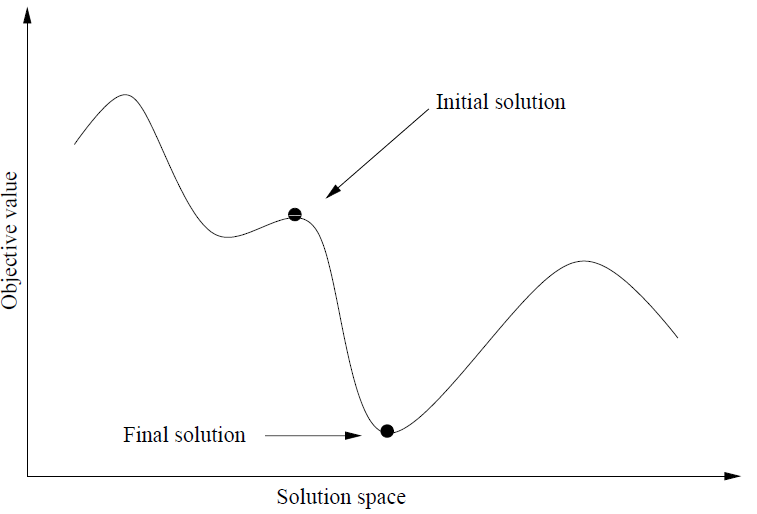
Plus grande descente
L’algorithme est principalement le même que pour la descente simple, seul un critère de sélection d’une solution voisine est modifié :
choose s' voisin de s / f(s') < f(s'') ou f(s')=f(s'') qqsoit s'' voisin de s
On choisit donc la solution voisine offrant la meilleure amélioration de la solution courant.
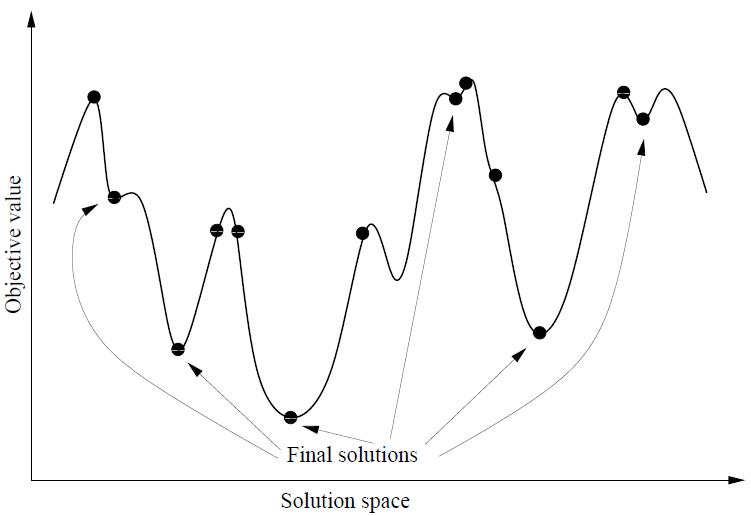
Descente multi-start
La descente multi-start effectue plusieurs instances du problème de descente simple ou de plus grande descente. L’algorithme est le suivant :
iter = 1 f(Best) = infini faire Choose a starting solution sO at random s 0) si f(s)<f(Best) alors Best tant que iter < iterMax retourne Bes