Algorithme naif / glouton / énumération

Contenus

Algorithme naif

Un algorithme naif a pour vocation de fournir un résultat de base à un problème. La méthode naïve ne fait aucun calcul préparatoire et se sert uniquement des données de base du problème.

Prenons pour exemple un problème du sac à dos. L’ algorithme naif consisterait à prendre en première les objets de la taille la plus petite jusqu’à ne plus pouvoir mettre de nouvel objet dans le sac.

pour i de 1 à n
   si w[i] + w_conso ≤ W alors
      x[i] := 1
      w_conso := w_conso + w[i]
   sinon
      x[i] := 0
   fin si
fin pour

Algorithme glouton (méthode intuitive)

Comme l’algorithme naif, un algorithme dit glouton se construit sur un principe simple : lors d’une itération, l’algorithme prend toujours la décision du « meilleur choix ». Il faut donc un choix localement optimal dans l’objectif que ce choix conduira à la solution optimale globale. Cependant, l’algorithme ne donne aucune garantie que la dernière solution soit une solution optimale.

Intuitivement, nous pouvons nous dire que pour maximiser l’utilité dans le problème du sac à dos, il suffit de mettre l’élément ayant la plus grande utilité (avec une taille compatible avec la taille restante dans le sac) jusqu’à ne plus avoir assez de place dans le sac.

Pour cela, nous allons considérer x et w les vecteurs du choix de l’objet et de son poids triés par ordre décroissant d’efficacité (efficacité = utilité/poids). Puis l’algorithme fonctionne comme la méthode naïve.

Un exemple simple permet de comprendre que ce choix n’est pas toujours optimal : prenons un objet de taille 1 et d’utilité 2, et un objet de taille et d’utilité égaux à la taille du sac. Dans ces conditions le premier objet à la plus grande utilité, il sera choisi en premier. Il n’y a plus de place pour placer le second objet. La solution optimale serait de choisir uniquement le deuxième objet dans le sac.

Force brute ou énumération

Contrairement à l’ algorithme naif, cette méthode garantit l’optimale globale, mais son temps d’exécution et sa consommation mémoire peuvent dépasser rapidement les limites d’un PC. Le principe est simple, il faut énumérer toutes les solutions possibles du problème et choisir la meilleure solution.

Généralement, l’arbre de solution est représenté comme le nom l’indique sous forme d’arbre. Prenons l’exemple du problème du sac à dos avec quatre objets avec les paramètres suivants et une taille de sac de 30 :

objet	1	2	3	4
u_i	7	3	4	3
w_i	13	8	12	10

L’arbre se construit par itération : à chaque itération, les nouvelles feuilles représentent le fait de prendre ou non le prochain objet. Nous obtenons l’arbre binaire suivant :

algorithme naïf algorithme glouton force brut énumération

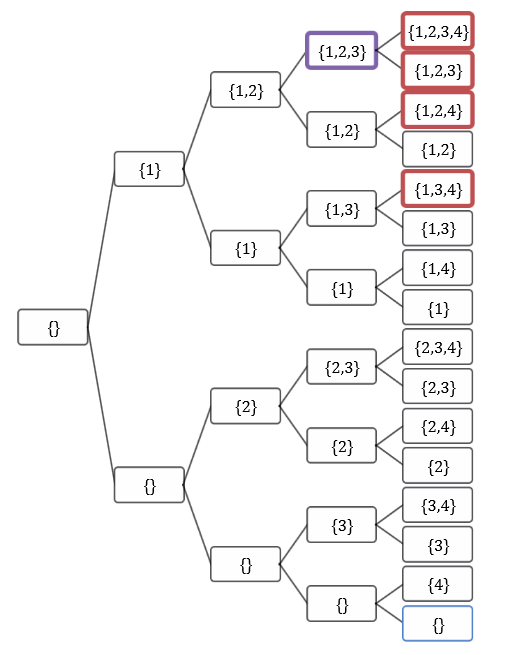
Les sommets en rouge dépasse la taille maximale du sac, le sommet en violet est la solution optimale. Comme vous pouvez le remarquer, le nombre de feuille est égale à 2^(n-1) pour l’objet n. Le nombre de nœuds générés jusqu’à l’objet n est donc 2ⁿ -1.