Complexité en temps

Contenus

La complexité en temps représente de façon asymptotique le temps que met un algorithme à trouver une solution.

Soit un problème P et M une méthode pour résoudre ce problème. L’algorithme est une description avec des structures de contrôle et de données permettant d’écrire la méthode M dans un langage reconnaissable par tout individu ou machine.

Pour rappel, les structures de contrôle sont : une séquence, un embranchement (ou sélection), une boucle (ou itération). Les structures de données sont : des constantes, des variables, des tableaux (ou espace de stockage ordonné), des structures récursives (listes, graphes etc).

Opération élémentaire

La complexité consiste à évaluer l’efficacité de la méthode M et de comparer cette dernière avec une autre méthode M’. Cette comparaison est indépendante de l’environnement (machine, système, compilateur, langage, etc). L’efficacité dépend du nombre d’opérations élémentaires. Ces dernières dépendent de la taille des données et de la nature des données.

Notons n la taille des données et T(n) le nombre d’opérations élémentaires. L’évaluation de efficacité se fera dans le meilleur des cas, le pire des cas et le cas moyen.

Dans le cas d’une structure de type séquence, l’évaluation est égale à la somme des coûts. Par exemple, si l’algorithme possède un traitement T1(n) suivit de T2(n), alors T(n)=T1(n)+T2(n).

Dans le cas d’un embranchement, l’évaluation est égale au maximum des embranchements. Par exemple, l’algorithme exécute T1(n) sinon T2(n), alors T(n)=max(T1(n), T2(n)).

Dans le cas d’une boucle, l’évaluation est égale à la somme des coûts des passages successifs. Par exemple, si l’algorithme est un « tant que faire Ti(n) avec la complexité de Ti(n) dépendant du numéro i de l’itération. Alors la complexité est T(n) = somme(i=1 à n) Ti(n).

Pour une version récursive, je vous invite à aller sur la page correspondante. Posons C(n) le traitement effectué dans une fonction en divide&conquer. Alors la complexité est T(n)=2*T(n/2)+C(n) = n log(n) si C(n)=n.

Notation de Landau

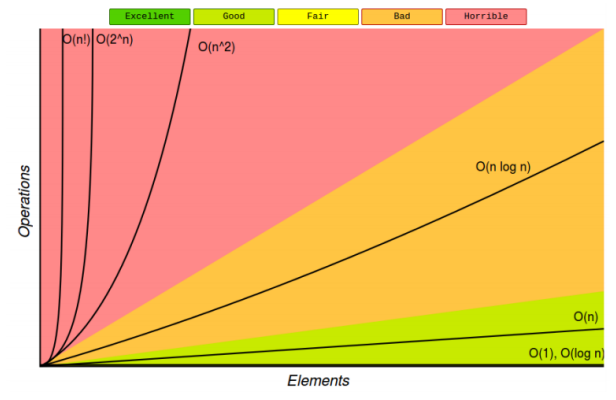
la notation de Landau caractérise le comportement asymptotique d’une fonction, c’est à dire le comportement de f(n) quand n tend vers l’infini.

On dit que f(n) est un grand O de g(n) si

\exists k>0, \exists n_0 \; \forall n>n_0 \; |f(n)| \leq |g(n)|\cdot k

complexité en temps big o notation de landau algorithme

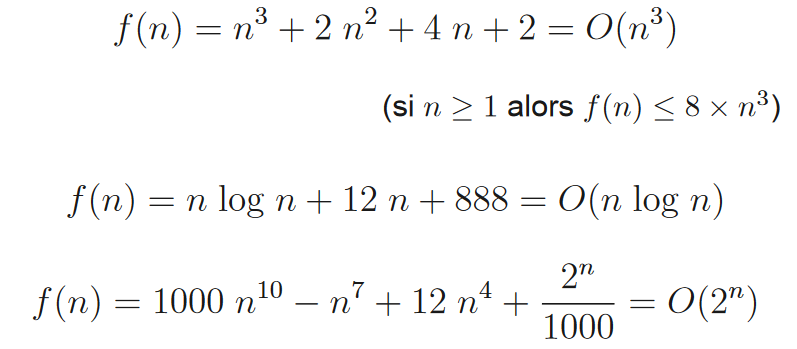
Exemples

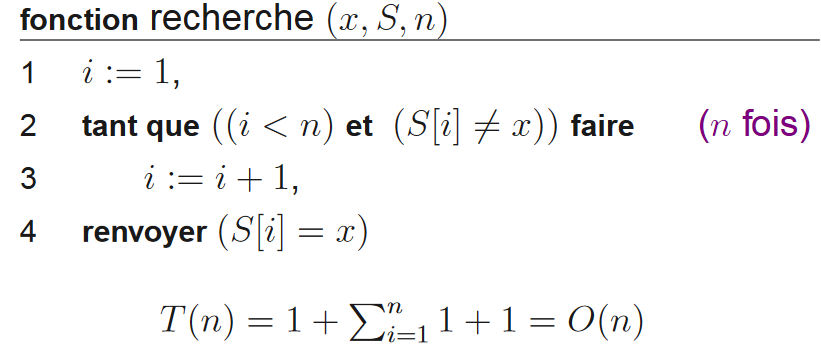
Pire, meilleur et moyenne

Nous pouvons calculer pour la plupart des algorithmes une complexité dans le pire des cas (le plus grand nombre d’opérations élémentaires), le meilleur et en moyenne. La moyenne est une somme pondérée par la probabilité de présence des complexités possibles. Le plus souvent, on utilise la complexité au pire car on souhaite connaitre une borne supérieur de temps d’exécution.

Considérons un algorithme de recherche d’un élément dans un tableau en forme itérative. L’algorithme s’arrête lorsque la valeur a été trouvée. L’algorithme se décompose ainsi : affectation de 0 à i, tant que i n’a pas parcouru le tableau on incrémente i, si tab[i]=valeur alors on retourne vrai, sinon à la fin du tableau on retourne faux. Notons C la complexité du corps de la boucle.

Au pire des cas, l’algorithme parcours tout le tableau, c’est à dire que T(n)=1+n*C=O(n). Au mieux, l’élément est au début du tableau, donc T(n)=1+C=O(1). Nous considérons qu’en moyenne, il y a 50% de chance que l’élément ne soit pas dans le tableau, et 50% qu’il soit à la moitié du tableau (ceci est bien entendu absurde, mais nous ne ferons pas toutes les possibilités). Dans ce cas, la complexité en moyenne est de T(n)=0.5*(1+n*C)+0.5*(1+n*C/2)=a*n+b avec a et b des constantes = O(n). Nous remarquons que le comportement asymptotique en moyenne est le même qu’au pire cas.

Exemples

Supposons que chacune des expressions ci-dessous donne le temps de traitement T(n) passé par un algorithme pour résoudre un problème de taille n. Sélectionnez le terme dominant (s) ayant la plus forte augmentation de n et spécifiez la complexité Big-Oh la plus basse de chaque algorithme.

Expression	Dominant	O(.)
5 + 0.001n³+ 0.025n	0.001n³	O(n³)
500n + 100n^1.5 + 50n log₁₀ n	100n^1.5	O(n^1.5)
0.3n + 5n^1.5 + 2.5 n^1.75	2.5 n^1.75	O(n^1.75)
n² log₂ n + n(log₂ n)²	n² log₂ n	O(n² log n)
n log₃ n + n log₂ n	n log₃ n, n log₂ n	O(n log n)
3 log₈ n + log₂ log₂ log₂ n	3 log₈ n	O(log n)
0. 100n + 0.01n²	0.01n²	O(n²)
0.01n + 100n²	100n²	O(n²)
2n + n^0.5 + 0.5n^1.25	0.5n^1.25	O(n^1.25)
0.01n log₂ n + n(log₂ n)²	n(log₂ n)²	O(n(log n)²)
100n log₃ n + n³ + 100n	n³	O(n³)

Les instructions ci-dessous montrent quelques caractéristiques de la notation « Big-Oh » pour les fonctions f ≡ f (n) et g ≡ g (n). Déterminez si chaque instruction est TRUE ou FALSE et corrigez la formule dans ce dernier cas.

Fonction	TRUE ou FALSE ?	Après correction
O(f + g) = O(f) + O(g)	FALSE	O(f + g) = max {O(f), O(g)}
O(f · g) = O(f) · O(g)	TRUE
if g = O(f) and h = O(f) then g = O(h)	FALSE	if g = O(f) and f = O(h) then g = O(h)
5n + 8n 2 + 100n 3 = O(n 4 )	TRUE
5n+8n 2 +100n 3 = O(n 2 log n)	FALSE	O(n³ )