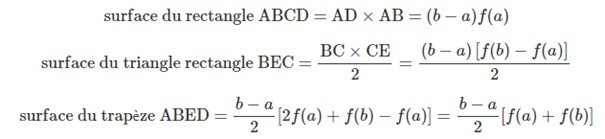Contenus
ToggleExercices corrigés avec algorithme en diviser pour régner
Les exercices corrigés suivants concernent la création d’algorithme selon la structure du diviser pour régner (divide&conquer). Les algorithmes de type dichotomie seront aussi étudiés.

Exercice 1
On va jouer au jeu du “plus petit, plus grand”. Le but est de deviner un nombre compris entre 1 et n (entier). On considère que l’algorithme prend en entrée la valeur de n et du nombre x à deviner, et qu’il retourne le nombre de coup pour trouver ce nombre.
a – Réexprimez le problème de façon plus formel.
b – Ecrire l’algorithme itératif résolvant ce problème.
c – Ecrire l’algorithme récursif résolvant ce problème.
d – Comparer les complexités.
a – Le problème pourrait se réécrire comme suit : Etant donné un tableau trié par ordre croissant d’entiers, comment déterminer si un élément appartient ou pas à ce tableau ? Le principe est bien connu : on compare l’élément recherché à l’élément médian, et le cas échéant on répète la recherche dans la partie gauche ou droite du tableau.
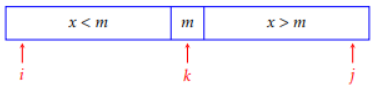
b – L’algorithme itératif est le suivant :

Puisque le tableau est coupé à chaque fois en deux, on parcourera au plus log n élément avant de trouver le bon ou de savoir qu’il n’existe pas. La complexité est donc O(log n)
c – Par défaut la réponse de l’algorithme est faux, sauf s’il y a un vrai qui est retournée ce qui donnera dans le main puis la méthode :

Puisque le fonctionnement est exactement le même que l’algorithme itératif, on se doute que la complexité est la même.
Exercice 2
On cherche la somme d’un tableau B de n éléments entiers.
1 – Écrivez un algorithme de type diviser-pour-régner qui résout ce problème.
2 – Analysez sa complexité et faire l’arbre d’appels pour le tableau [3,4,2,3,4].
3 – Comparez-la avec un algorithme itératif que vous décrirez
On définit la fonction Sum(B,i,j) qui est la somme des éléments de B entre les positions i et j. Ainsi la valeur recherchée est Sum(B,1,n). On va calculer Sum(B,i,j) en découpant le tableau B[i..j] en deux moitiés ; calculant les sommes pour chaque moitié ; et additionnant ces deux sommes. Ceci donne le code suivant :

Pour la complexité, vu qu’on n’a pas encore vu le Master Theorem on va se servir de l’arbre d’appels :

On comprend que l’on coupe en deux à chaque fois le tableau. Le calcul est simple, donc la complexité ne dépend que de la profondeur de l’arbre p tel que 2^p > n (taille du tableau) d’où p > log n et une complexité en O(log n).
L’algorithme itératif est le suivant :

Ici la complexité est de O(n).
Exercice 3
On dit qu’un tableau a un élément majoritaire si une valeur du tableau est présent au moins n/2 fois sur n éléments.
1 – Proposer un algorithme itératif pour résoudre ce problème.
2 – Proposer une méthode pour résoudre ce problème en diviser pour régner.
3 – Ecrire la méthode décrite par un algorithme.
Modifier votre algorithme en tenant compte des propriétés suivantes :
- si une seule des moitiés fournit un majoritaire, seul cet élément peut être majoritaire dans le tableau complet.
- si les deux appels récursifs fournissent des majoritaires, qu’ils sont différents, avec un nombre d’occurrences différent : le seul qui puisse être majoritaire est celui qui a la plus grand nombre d’occurrences.
- dans le cas où n est une puissance de 2, et donc les moitiés toujours de taille égale, s’il y a deux majoritaires différents avec le même nombre d’occurrences, alors il ne peut y avoir de majoritaire dans le tableau complet.
1 – On compte le nombre d’occurrence de chaque élément (pas besoin de compter vers la gauche car s’il existe alors il a déjà été compté auparavant). Pour la première boucle, on aurait pu s’arrêter à n/2 + 1 car même si tous les éléments suivant étaient identique il ne serait tout de même pas majoritaire.

2 – On va partir du principe de diviser pour régner :
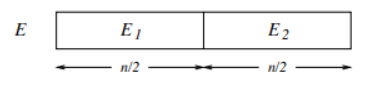
S’il existe un élément majoritaire x dans E, alors x est majoritaire dans au moins une des deux listes E1 et E2 (en effet si x non majoritaire dans E1, ni dans E2, alors dans E, nombre de x ≤ n/4 + n/4 = n/2).
Le principe de la récursion est alors le suivant : calculer les éléments majoritaires de E1 et de E2 (s’ils existent) avec le nombre total d’occurrences de chacun et en déduire si l’un des deux est majoritaire dans E.
L’algorithme suivant Majoritaire(i, j) renvoie un couple qui vaut (x, cx) si x est majoritaire dans le sous-tableau E[i..j] avec cx occurrences et qui vaut (−, 0) s’il n’y a pas de majoritaire dans E[i..j], l’appel initial étant Majoritaire(1, n). La fonction Occurence(x, i, j) calcule le nombre d’occurrences de x dans le sous-tableau E[i..j].

Il n’est pas si facile à comprendre, prenons un exemple d’un tableau de 8 éléments avec 5 éléments identiques pour bien comprendre son fonctionnement.
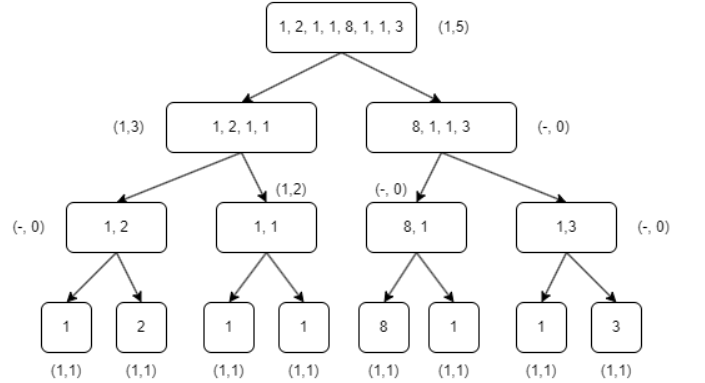
Voici l’algorithme majoritaire en tenant compte des nouvelles propriétés :

Exercice 4
1 – Proposer un algorithme en diviser pour régner cherchant le minimum d’un tableau.
2 – De même avec le maximum.
3 – De même en recherchant à la fois le minimum et le maximum.
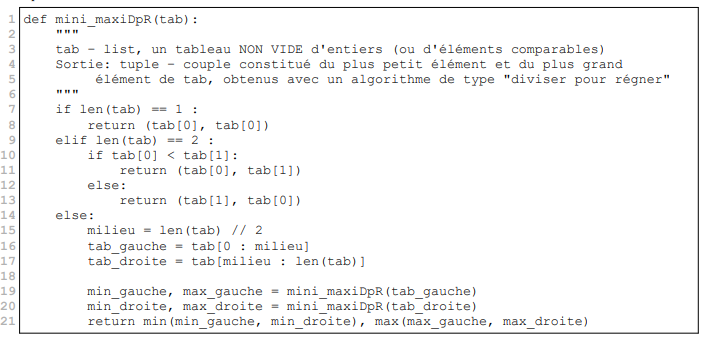
Je vais donner directement la réponse à la question 3 puisqu’elle contient la réponse aux deux précédentes. Dans cette méthode, il faut retenir les positions dans le tableau ainsi que la valeur de min et max.
Exercice 5
Voici la formule du produit matricielle :
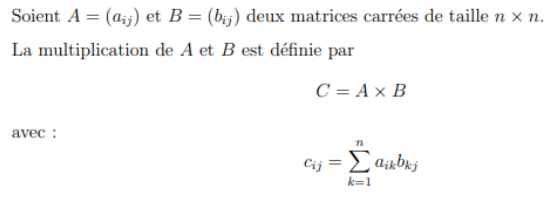
1 – Proposer un algorithme itératif et en donner la complexité.
Pour décomposer une matrice en dichotomie, il faut le faire à la fois sur les lignes et sur les colonnes, donc en 4 parties comme le schéma suivant :
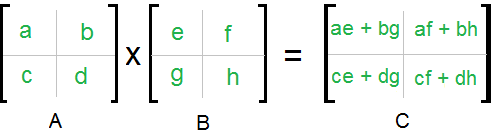
Chaque élément est une matrice carrée. Notons r=ae+bg, s=af+bh, t=ce+dg et u=cf+dh.
2 – Strassen a trouvé une méthode pour encore réduire le nombre de calcul. Il propose de calculer r, s, t, u en utilisant une combinaison linéaire (addition ou soustraction) des matrices suivantes :

Exprimer r, s, t, u en fonction des pi.
3 – Proposer un algorithme récursif basé sur les calculs de Strassen pour le produit matricielle.
1 – On remarque dans la formule qu’il va falloir faire trois boucles en fonction de i, j et k.

Au plus profond des structures à itérations, il y a trois boucles de 1 à n imbriquées, donc une complexité en O(n^3)
2 – Cela donne les relations linéaires suivantes :
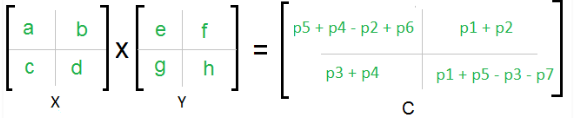
3 – L’algorithme en diviser pour régner est le suivant :

Exercice 6
Écrivez un pseudo-code pour un algorithme Diviser pour Régner permettant de trouver la position du plus grand élément dans un tableau de nombres. Écrivez un pseudo-code pour un algorithme de force brute, comparez avec le précédent. Montrez un arbre du processus de l’algorithme diviser pour mieux régner. Quel est le niveau maximal de l’arborescence pour les nombres ?

L’algorithme de force brute est trivial : une boucle.
A chaque niveau l, l’arbre binaire complet est composé de 2^(l-1) feuille. Donc le total des sommets est 2^l -1. Soit l le niveau de l’arbre, donc l=sup(log_2 (n)).
Exercice 7
Écrivez un pseudo-code pour un algorithme de division pour régner pour le problème d’exponentiation du calcul de a^n où a>0 et n est un entier positif. Écrivez un pseudo-code pour un algorithme de force brute, comparez avec le précédent. Montrez un arbre du processus de l’algorithme diviser pour mieux régner. Quel est le niveau maximum de l’arbre pour n non donné ? Vérifier la terminaison, l’exactitude et l’exhaustivité.
Exercice 8
Pour multiplier deux nombres entiers de n chiffres, une méthode naïve consiste à multiplier chaque chiffre du premier nombre par chaque chiffre du second, et de faire les bons décalages et les bonnes sommes. Le temps de calcul est alors en O(n²).
L’algorithme de Karatsuba utilise le principe que le calcul utilisé dans cette approche naïve :
(a × 10^k+ b)(c × 10k+ d) = ac × 10^2k+ (ad + bc) × 10^k+ bd
nécessitant quatre produits (ac, ad, bc et bd) peut être fait avec seulement trois produits en regroupant les calculs sous la forme suivante :
(a × 10^k + b)(c × 10^k + d) = ac × 10^2k + (ac + bd − (a − b)(c − d)) × 10^k + bd
Certes des soustractions ont été introduites, mais seulement trois produits de grands nombres sont maintenant nécessaires : ac, bd et (a − b)(c − d).
Comme les additions et les soustractions sont peu coûteuses (négligeables par rapport aux multiplications), nous allons gagner en temps de calcul. Pour information la multiplication par une puissance de la base de calcul correspond à un décalage de chiffre et est très rapide à exécuter sur une machine.
Écrire le code de la fonction karatsuba() permettant de multiplier deux grands nombres entiers de n chiffres selon ce principe.
Exercice 9
Etant donné un ensemble de points réels, trouver la distance minimale entre deux points en utilisant un algorithme de type Diviser pour régner. Pour cela on utilisera la distance Euclidienne entre deux points.
La solution évidente est de réaliser une matrice de distance entre chaque pair de points. L’algorithme de diviser pour régner coupe l’espace récursivement en 2 blocs et regarde la distance minimale dans chaque blocs. De plus, il faut ensuite regarder la plus petite distance entre points de deux blocs différents.
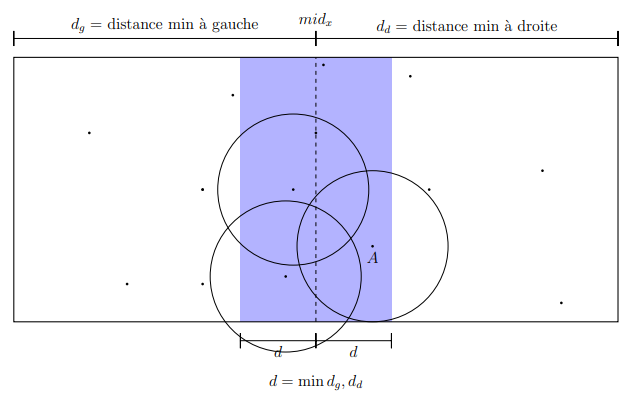
Solution diviser-pour-régner
— Trier les points relativement à leurs coordonnées x.
— Diviser les points en deux groupes : la moitié gauche et la moitié droite.
— Utiliser la récursion pour trouver dg, la distance min entre les points de
gauche.
— Utiliser la récursion pour trouver dd, la distance min entre les points de droite.
— La solution optimale est :
— soit dg,
— soit dd,
— soit la distance entre deux points A et B tels que A est dans la partie
gauche et B est dans la partie droite.
Soit midx la coordonnée x du point le plus à droite parmi les points de gauche. On remarque que dans le troisième cas cité ci-dessus, les deux points A et B se situent dans une fine bande de largeur min(dg, dd), centrée en midx.
On remarque dans la bande centrale, deux points situées du même côté de la
frontière midx sont au moins à distance d l’un de l’autre. On exploite cette information de la manière suivante :
— On commence par trier tous les points présents dans la bande centrale en fonction de leur coordonnée y.
— Pour chaque point A dans la bande centrale, on regarde la distance qui le sépare des points se trouvant dans son rayon.

Exercice 10
On s’intéresse dans cet exercice à la complexité dans le pire des cas et en nombre de comparaisons des algorithmes.
1. Pour rechercher le plus grand et deuxième plus grand élément de n entiers, donner un algorithme naïf et sa complexité.
2. Pour améliorer les performances, on se propose d’envisager la solution consistant à calculer le maximum selon le principe de Diviser pour Régner
1.

2.
Le principe est assez simple puisque cela est proche de l’algorithme Merge Sort. Lors du règne, un tuple de deux éléments est remonté (max1, max2) ou max1 > max2. Le règne consiste à comparer les tuples gauche et droit et de retourner les deux plus grands. Ainsi, chaque branche retournera les deux plus grands de son sous-tableau jusqu’à obtenir les deux plus grands du tableau dans son entièreté.
Exercice 11
Étant donné un tableau d’entiers, trouvez la somme maximale parmi tous les sous-tableaux possibles. Les sous-tableaux doivent occuper des positions consécutives dans le tableau d’origine.
Entrée : nombres[] = [2, -4, 1, 9, -6, 7, -3]
Sortie : la somme maximale du sous-tableau est de 11 (marquée en gras)
L’idée est d’utiliser la technique Divide and Conquer pour trouver la somme maximale des sous-tableaux. L’algorithme fonctionne comme suit:
- Divisez le tableau en deux sous-tableaux égaux.
- Calculer récursivement la somme maximale des sous-tableaux pour le sous-tableau gauche,
- Calculer récursivement la somme maximale des sous-tableaux pour le sous-tableau droit,
- Trouvez la somme maximale du sous-tableau qui traverse l’élément du milieu.
- Renvoie le maximum des trois sommes ci-dessus.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 | #include <stdio.h> #include <limits.h> // Utility function to find the maximum of two numbers int max(int x, int y) { return (x > y) ? x : y; } // Function to find the maximum subarray sum using divide-and-conquer int maximum_sum(int nums[], int low, int high) { // If the array contains 0 or 1 element if (high <= low) { return nums[low]; } // Find the middle array element int mid = (low + high) / 2; // Find maximum subarray sum for the left subarray, // including the middle element int left_max = INT_MIN; int sum = 0; for (int i = mid; i >= low; i—) { sum += nums[i]; if (sum > left_max) { left_max = sum; } } // Find maximum subarray sum for the right subarray, // excluding the middle element int right_max = INT_MIN; sum = 0; // reset sum to 0 for (int i = mid + 1; i <= high; i++) { sum += nums[i]; if (sum > right_max) { right_max = sum; } } // Recursively find the maximum subarray sum for the left // and right subarray, and take maximum int max_left_right = max(maximum_sum(nums, low, mid), maximum_sum(nums, mid + 1, high)); // return the maximum of the three return max(max_left_right, left_max + right_max); } int main(void) { int arr[] = { 2, –4, 1, 9, –6, 7, –3 }; int n = sizeof(arr) / sizeof(arr[0]); printf(« The maximum sum of the subarray is %d », maximum_sum(arr, 0, n – 1)); return 0; } |
Nous pouvons facilement résoudre ce problème en temps linéaire en utilisant l’algorithme de Kadane. L’idée est de maintenir un sous-tableau maximum (somme positive) « se terminant » à chaque index du tableau donné. Ce sous-tableau est soit vide (auquel cas sa somme est nulle) soit constitué d’un élément de plus que le sous-tableau maximum se terminant à l’indice précédent.
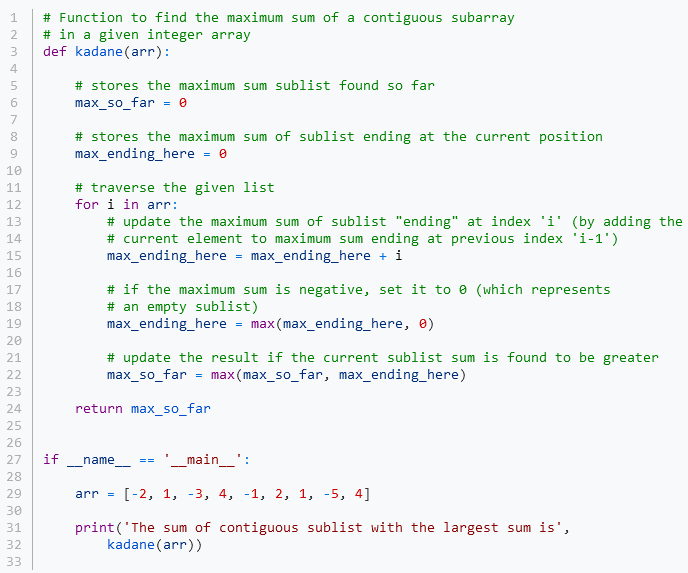
Exercice 12
Étant donné un tableau d’entiers, trouvez l’élément de pic qu’il contient. Un élément de pic est un élément supérieur à ses voisins. Il peut y avoir plusieurs éléments de pic dans un tableau et la solution doit signaler tout élément de pic.
Un élément A[i] d’un tableau A est un élément de pic s’il n’est pas plus petit que son ou ses voisins.
A[i-1] <= A[i] >= A[i+1] pour 0 < i < n-1
A[i-1] <= A[i] si je = n – 1
A[i] >= A[i+1] si je = 0
Par exemple,
Entrée : [8, 9, 10, 2, 5, 6]
Sortie : l’élément de pic est 10 (ou 6)
Entrée : [8, 9, 10, 12, 15]
Sortie : l’élément de pic est 15
Entrée : [10, 8, 6, 5, 3, 2]
Sortie : l’élément de pic est 10
Une solution naïve serait de tester tous les éléments pour le pic en exécutant une recherche linéaire sur le tableau et de renvoyer l’élément le plus grand que ses voisins. Deux cas particuliers doivent être traités. Si le tableau est trié par ordre décroissant, son élément de pic est le premier élément. Si le tableau est trié par ordre croissant, l’élément de pic est le dernier. Le problème avec cette approche est que sa complexité temporelle dans le pire des cas est O(n), où n est la taille de l’entrée.
Nous pouvons facilement résoudre ce problème en temps O(log(n)) en utilisant une idée similaire à l’algorithme de recherche binaire. L’idée est de calculer l’indice médian, et si l’élément du milieu est supérieur à ses deux voisins, renvoyez l’élément car il s’agit d’un pic. Si le voisin droit de l’index médian est supérieur à l’élément du milieu, recherchez de manière récursive le pic sur le côté droit du tableau. Si le voisin gauche de l’index médian est supérieur à l’élément du milieu, recherchez de manière récursive le pic dans le côté gauche du tableau.

Exercice 13
Étant donné un tableau trié avec éventuellement des éléments en double, la tâche consiste à trouver les index des première et dernière occurrences d’un élément x dans le tableau donné.
Exemples:
Entrée : tab[] = {1, 3, 5, 5, 5, 5, 67, 123, 125}, x = 5
Sortie : Première occurrence = 2
Dernière occurrence = 5
Entrée : tab[] = {1, 3, 5, 5, 5, 5, 7, 123, 125 }, x = 7
Sortie : Première occurrence = 6
Dernière occurrence = 6
L’idée pour résoudre ce problème est d’itérer sur les éléments d’un tableau donné et de vérifier les éléments donnés dans un tableau et de garder une trace de la première et de la dernière occurrence de l’index de l’élément trouvé.
Exécutez une boucle for et for i = 0 to n-1
Prendre premier = -1 et dernier = -1
Lorsque nous trouvons un élément pour la première fois, nous mettons d’abord à jour = i
Nous mettons toujours à jour last=i chaque fois que nous trouvons l’élément.
Nous imprimons en premier et en dernier.

Une approche efficace utilisant la recherche binaire :
1. Pour la première occurrence d’un nombre
a) Si (élevé >= faible)
b) Calculer moyen = faible + (élevé – faible)/2 ;
c) Si ((milieu == 0 || x > arr[milieu-1]) && arr[milieu] == x)
retour milieu;
d) Sinon si (x > arr[moyen])
retourner premier(arr, (moyen + 1), haut, x, n);
e) Sinon
return first(arr, low, (mid -1), x, n);
f) Sinon retourner -1 ;
2. Pour la dernière occurrence d’un nombre
a) si (haut >= bas)
b) calculer moyen = faible + (élevé – faible)/2 ;
c)if( ( milieu == n-1 || x < arr[milieu+1]) && arr[milieu] == x )
retour milieu;
d) sinon si(x < arr[milieu])
return last(arr, low, (mid -1), x, n);
e) d’autre
return last(arr, (mid + 1), high, x, n);
f) sinon retourner -1 ;

Exercice 14
Étant donné n bâtiments rectangulaires dans une ville en 2 dimensions, calcule la ligne d’horizon de ces bâtiments, en éliminant les lignes cachées. La tâche principale consiste à visualiser les bâtiments d’un côté et à supprimer toutes les sections non visibles.
Tous les bâtiments partagent un fond commun et chaque bâtiment est représenté par un triplet (gauche, ht, droite)
‘gauche’ : est la coordonnée x du côté gauche (ou du mur).
‘right’ : est la coordonnée x du côté droit
‘ht’ : est la hauteur du bâtiment.
Une ligne d’horizon est un ensemble de bandes rectangulaires. Une bande rectangulaire est représentée par une paire (gauche, ht) où gauche est la coordonnée x du côté gauche de la bande et ht est la hauteur de la bande.
Exemples:
Entrée : tableau de bâtiments
{ (1, 11, 5), (2, 6, 7), (3, 13, 9), (12, 7, 16), (14, 3, 25),
(19, 18, 22), (23, 13, 29), (24, 4, 28) }
Sortie : Skyline (un ensemble de bandes rectangulaires)
Une bande a la coordonnée x du côté gauche et de la hauteur
(1, 11), (3, 13), (9, 0), (12, 7), (16, 3), (19, 18),
(22, 3), (25, 0)
L’image ci-dessous est pour l’entrée 1 :

Nous pouvons trouver Skyline en temps Θ(nLogn) en utilisant Divide and Conquer. L’idée est similaire à Merge Sort, diviser l’ensemble donné de bâtiments en deux sous-ensembles. Construisez récursivement l’horizon pour deux moitiés et fusionnez enfin les deux horizons.
L’idée est similaire à la fusion du tri par fusion, commencez par les premières bandes de deux horizons, comparez les coordonnées x. Choisissez la bande avec la plus petite coordonnée x et ajoutez-la au résultat. La hauteur de la bande ajoutée est considérée comme le maximum des hauteurs actuelles de skyline1 et skyline2.
La hauteur de la nouvelle bande est toujours obtenue en prenant au maximum les suivants
(a) Hauteur actuelle de skyline1, dites ‘h1’.
(b) Hauteur actuelle de skyline2, dites ‘h2’
h1 et h2 sont initialisés à 0. h1 est mis à jour lorsqu’une bande de SkyLine1 est ajoutée au résultat et h2 est mis à jour lorsqu’une bande de SkyLine2 est ajoutée.
Skyline1 = {(1, 11), (3, 13), (9, 0), (12, 7), (16, 0)}
Skyline2 = {(14, 3), (19, 18), (22, 3), (23, 13), (29, 0)}
Résultat = {}
h1 = 0, h2 = 0
Comparez (1, 11) et (14, 3). Étant donné que la première bande a un x gauche plus petit, ajoutez-le au résultat et incrémentez l’index pour Skyline1.
h1 = 11, nouvelle hauteur = max(11, 0)
Résultat = {(1, 11)}
Comparez (3, 13) et (14, 3). Étant donné que la première bande a un x gauche plus petit, ajoutez-le au résultat et incrémentez l’index pour Skyline1
h1 = 13, nouvelle hauteur = max(13, 0)
Résultat = {(1, 11), (3, 13)}
De même (9, 0) et (12, 7) sont additionnés.
h1 = 7, nouvelle hauteur = max(7, 0) = 7
Résultat = {(1, 11), (3, 13), (9, 0), (12, 7)}
Comparez (16, 0) et (14, 3). Étant donné que la deuxième bande a un x gauche plus petit, elle est ajoutée au résultat.
h2 = 3, nouvelle hauteur = max(7, 3) = 7
Résultat = {(1, 11), (3, 13), (9, 0), (12, 7), (14, 7)}
Comparez (16, 0) et (19, 18). Puisque la première bande a un x gauche plus petit, elle est ajoutée au résultat.
h1 = 0, nouvelle hauteur = max(0, 3) = 3
Résultat = {(1, 11), (3, 13), (9, 0), (12, 7), (14, 7), (16, 3)}
Puisque Skyline1 n’a plus d’éléments, tous les éléments restants de Skyline2 sont ajoutés
Résultat = {(1, 11), (3, 13), (9, 0), (12, 7), (14, 7), (16, 3),
(19, 18), (22, 3), (23, 13), (29, 0)}
Une observation concernant la sortie ci-dessus est que la bande (14, 7) est redondante (il existe déjà une bande de même hauteur). Nous supprimons tous les éléments redondants
bandes.
Résultat = {(1, 11), (3, 13), (9, 0), (12, 7), (16, 3), (19, 18),
(22, 3), (23, 13), (29, 0)}
Dans le code ci-dessous, la redondance est gérée en n’ajoutant pas de bande si la bande précédente dans le résultat a la même hauteur.


Exercice 15
Étant donné un tableau de citations d’entiers où citations[i] est le nombre de citations qu’un chercheur a reçues pour son ième article et les citations sont triées par ordre croissant, retournez calculer l’index h du chercheur.
Selon la définition de h-index sur Wikipedia : un scientifique a un index h si h de ses n articles ont au moins h citations chacun, et les autres n − h articles n’ont pas plus de h citations chacun.
S’il existe plusieurs valeurs possibles pour h, la valeur maximale est prise comme indice h.
Entrée : citations = [0,1,3,5,6]
Sortie : 3
Explication : [0,1,3,5,6] signifie que le chercheur a 5 articles au total et chacun d’eux a reçu respectivement 0, 1, 3, 5, 6 citations.
Étant donné que le chercheur a 3 articles avec au moins 3 citations chacun et les deux autres avec pas plus de 3 citations chacun, leur h-index est de 3.
Juste une recherche binaire, à chaque fois vérifier les citations[mid]
cas 1 : citations[mid] == len-mid, alors cela signifie qu’il y a des citations[mid] articles qui ont au moins citations[mid] citations.
cas 2 : citations[mid] > len-mid, alors cela signifie qu’il y a des citations[mid] articles qui ont plus de citations[mid] citations, donc nous devrions continuer à chercher dans la moitié gauche
cas 3 : citations[mid] < len-mid, il faut continuer la recherche dans la partie droite
Après itération, il est garanti que right+1 est celui que nous devons trouver (c’est-à-dire que len-(right+1) papiers a au moins len-(righ+1) citations)
L’algorithme suivant est écrit sous forme itérative mais c’est bien du Diviser pour Régner :

Exercice 16
Dans le problème « Koko Eating Bananas », on nous donne un tableau de taille n qui contient le nombre de bananes dans chaque tas. En une heure, Koko peut manger au maximum K bananes. Si le tas contient moins de K bananes, dans ce cas si Koko termine toutes les bananes de ce tas, elle ne peut pas commencer à manger des bananes d’un autre tas dans la même heure.
Koko veut manger toutes les bananes en H heures. Nous sommes censés trouver la valeur minimale de K.
piles = [30,11,23,4,20], H = 6. Ici la réponse est 23.

Koko mangera des bananes de cette manière pour manger toutes les bananes en 6 heures :
Première heure : 23
Deuxième heure : 7
Troisième heure : 11
Quatrième heure : 23
Cinquième heure : 4
Sixième heure : 20
La première et la plus importante chose pour résoudre ce problème est de faire ressortir des observations. Voici quelques observations pour notre intervalle de recherche :
Koko doit manger au moins une banane par heure. C’est donc la valeur minimale de K. nommons-le comme Start
Nous pouvons limiter le nombre maximum de bananes que Koko peut manger en une heure au nombre maximum de bananes dans un tas parmi tous les tas. Il s’agit donc de la valeur maximale de K. Appelons-la End.
Nous avons maintenant notre intervalle de recherche. Supposons que la taille de l’intervalle soit Longueur et que le nombre de piles soit n. L’approche naïve pourrait être de vérifier chaque valeur dans l’intervalle. si pour cette valeur de K Koko peut manger toutes les bananes en heure H avec succès, choisissez le minimum d’entre elles. La complexité temporelle pour l’approche naïve sera Longueur*n dans le pire des cas.
Nous pouvons améliorer la complexité temporelle en utilisant la recherche binaire à la place de la recherche linéaire. L’algorithme est écrit en itératif mais il s’agit bien d’une approche Diviser pour Régner
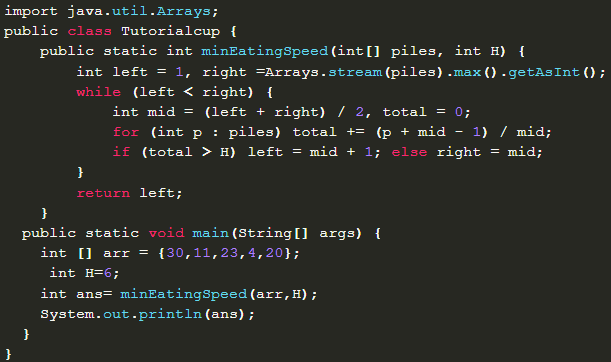
Exercice 17
Étant donné un tableau trié d’entiers distincts non négatifs, trouvez le plus petit élément non négatif manquant dans celui-ci.
Par exemple,
Entrée : nombres[] = [0, 1, 2, 6, 9, 11, 15]
Résultat : Le plus petit élément manquant est 3
Entrée : nombres[] = [1, 2, 3, 4, 6, 9, 11, 15]
Sortie : le plus petit élément manquant est 0
Entrée : nombres[] = [0, 1, 2, 3, 4, 5, 6]
Résultat : Le plus petit élément manquant est 7
Une solution naïve consisterait à exécuter une recherche linéaire sur le tableau et à renvoyer le premier index, qui ne correspond pas à sa valeur. Si aucune discordance ne se produit, renvoyez la taille du tableau. Le problème avec cette approche est que sa complexité temporelle dans le pire des cas est O(n), où n est la taille de l’entrée. Cette solution ne profite pas non plus du fait que l’entrée est triée.
Nous pouvons facilement résoudre ce problème en temps O(log(n)) en modifiant l’algorithme de recherche binaire (équivalent au Diviser pour Régner). L’idée est de comparer l’indice médian avec l’élément médian. Si les deux sont identiques, alors la non-concordance se trouve dans le bon sous-tableau ; sinon, il se trouve dans le sous-tableau de gauche. Donc, nous écartons une moitié en conséquence et revenons pour l’autre.
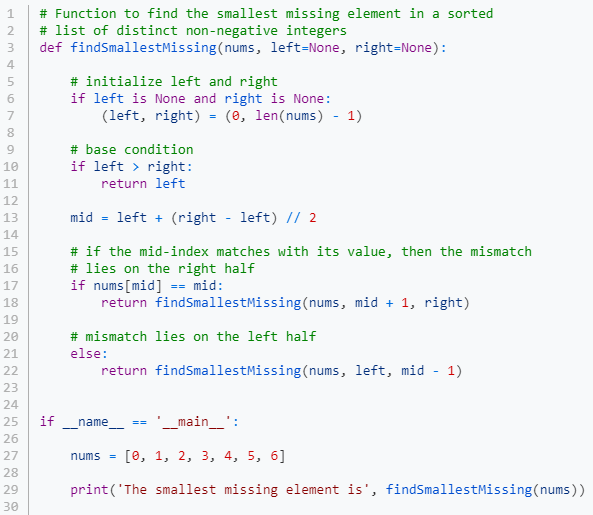
Exercice 18
Étant donné un tableau d’entiers nums et un entier k, renvoie le kème plus grand élément du tableau.
Notez qu’il s’agit du kème élément le plus grand dans l’ordre trié, et non du kème élément distinct.
Vous devez le résoudre en complexité temporelle O(nlogn).
Exemple 1:
Entrée : nombres = [3,2,1,5,6,4], k = 2
Sortie : 5
Exemple 2 :
Entrée : nombres = [3,2,3,1,2,4,5,5,6], k = 4
Sortie : 4
Pour résoudre ce problème il faut aller au plus simple. Trier le tableau en O(nlogn) puis le parcourir du plus grand au plus petit. Un compteur s’incrémente dès qu’on change de nombre, on retourne le nombre du k-ième changement.
Exercice 19
Étant donné un tableau d’entiers nums, renvoyer un tableau d’entiers counts où counts[i] est le nombre d’éléments plus petits à droite de nums[i].
Entrée : nombres = [5,2,6,1]
Sortie : [2,1,1,0]
Explication:
À droite de 5, il y a 2 éléments plus petits (2 et 1).
A droite de 2, il n’y a qu’un seul élément plus petit (1).
À droite de 6, il y a 1 élément plus petit (1).
À droite de 1, il y a 0 élément plus petit.
Les plus petits nombres à droite d’un nombre sont exactement ceux qui sautent de sa droite à sa gauche lors d’un tri stable. Je fais donc un tri par fusion avec un suivi supplémentaire de ces sauts de droite à gauche. Voici les algorithmes sous leur forme itérative.
On trie les paires (index, valeur). La valeur est utilisée pour le tri et l’index est utilisé pour le suivi des sauts.
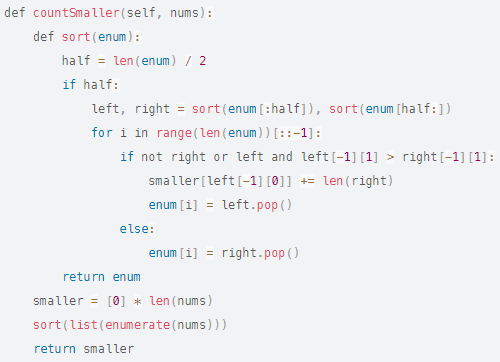
Vous pouvez également trier uniquement les index et rechercher les chiffres réels pour les comparaisons à la volée. Peut-être un peu plus facile à comprendre et à porter dans d’autres langues :

Exercice 20
Étant donné deux tableaux triés nums1 et nums2 de taille m et n respectivement, renvoie la médiane des deux tableaux triés.
La complexité globale du temps d’exécution doit être O(log (m+n)).
Exemple 1:
Entrée : nums1 = [1,3], nums2 = [2]
Sortie : 2.00000
Explication : tableau fusionné = [1,2,3] et la médiane est 2.
Exemple 2 :
Entrée : nums1 = [1,2], nums2 = [3,4]
Sortie : 2.50000
Explication : tableau fusionné = [1,2,3,4] et la médiane est (2 + 3) / 2 = 2,5.
Voyons d’abord le concept de ‘MÉDIAN’ d’une manière un peu non conventionnelle. C’est-à-dire:
« si nous coupons le tableau trié en deux moitiés de LONGUEURS ÉGALES, alors la médiane est la MOYENNE DE Max(lower_half) et Min(upper_half), c’est-à-dire les deux nombres immédiatement à côté de la coupe ».
Par exemple, pour [2 3 5 7], on fait la coupure entre 3 et 5 :
[2 3 / 5 7]
alors la médiane = (3+5)/2.
Voici l’algorithme en Diviser pour Régner :

trouver le kième élément dans les deux tableaux triés : A[aMid] <= B[bMid], x : mi-longueur de a, y : mi-longueur de b, alors on peut savoir
(1) il y aura au moins (x + 1 + y) éléments avant bMid
(2) il y aura au moins (m – x – 1 + n – y) = m + n – (x + y +1) éléments après aMid
Donc
si k <= x + y + 1, trouver le kème élément dans a et b, mais sans tenir compte de bMid et de son suffixe
si k > x + y + 1, trouver le k – (x + 1) ème élément dans a et b, mais sans considérer aMid et son préfixe

Exercice 21
Votre tâche consiste à calculer a^b mod 1337 où a est un entier positif et b est un entier positif extrêmement grand donné sous la forme d’un tableau.
Une connaissance : ab % k = (a%k)(b%k)%k
Puisque la puissance ici est un tableau, nous ferions mieux de la gérer chiffre par chiffre. Un constat :
a^1234567 % k = (a^1234560 % k) * (a^7 % k) % k = (a^123456 % k)^10 % k * (a^7 % k) % k
Ça vous paraît compliqué ? Permettez-moi de le dire autrement:
Supposons que f(a, b) calcule a^b % k ; Traduisez ensuite la formule ci-dessus en utilisant f :
f(a,1234567) = f(a, 1234560) * f(a, 7) % k = f(f(a, 123456),10) * f(a,7)%k ;
Mise en œuvre de cette idée :

Exercice 22
Pour calculer l’aire sous la courbe, il est possible d’encadrer la courbe par un rectangle et d’en déduire que l’aire de la courbe est dans l’ordre de grandeur de l’aire du rectangle.
La méthode des rectangles est une méthode algorithmique qui permet d’obtenir un encadrement d’une intégrale. Pour rappel ; une fonction positive sur un intervalle [a,b], à pour intégrale sur cet intervalle l’aire sous la courbe représentative de f et l’axe des abscisses.
Dans l’algorithme Diviser pour Régner, on subdivise l’intervalle [a,b] en n intervalles de largueur inférieur à un seuil k (k étant la précision de calcul de l’intégral).
Soit I le milieu d’un intervalle, l’aire sous la courbe dans cet intervalle est donc égale au rectangle dont la hauteur est définie par f(I). L’aire dans l’intervalle d’origine est donc égale à la somme de toutes les aires subdivisées.
Il est aussi possible d’encadrer l’aire sous la courbe en considérant qu’elle est de même grandeur que la somme des rectangles de hauteur f(a) et de même grandeur que la somme des rectangles de hauteur f(b).
Une troisième méthode existe pour simuler l’aire sous la courbe : la méthode des trapèzes.
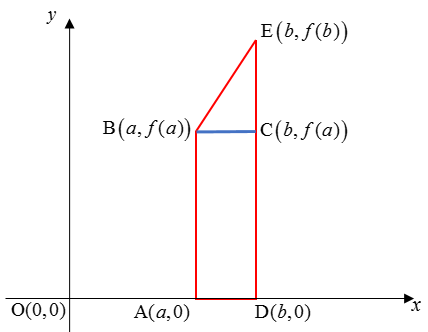
Pour calculer la surface du trapèze ABED, on fait la somme des aires du rectangle ABCD et du triangle rectangle BEC. L’aire du trapèze est une représentation de l’aire sous la courbe dans l’intervalle [a,b].
Les algorithmes sont très simple. Tant que la taille seuil n’est pas atteinte, on renvoie methode(a, (a+b)/2, fonction) + methode ((a+b)/2, b, fonction).
Ce calcul permet de sommer les parties gauche et droite de la diviser de l’intervalle. Une fois le seuil atteint, la méthode renvoie le calcul de l’aire correspondant à l’énoncé étudié.
Pour les rectangles dit à droite nous aurons comme somme totale :
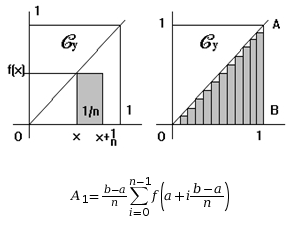
Pour les rectangles dit à gauche nous aurons comme somme totale :

Pour la méthode des trapèzes, le calcul de chaque sous-intervalle est donné par la formule suivante :