Contenus
ToggleExercices corrigés sur les algorithmes de tri
Les exercices corrigés suivants concernent les algorithmes de tri : Tri par sélection, tri par insertion, tri à bulles, tri cocktail, tri rapide et tri fusion.

Les tris itératifs : tri par sélection
Sur un tableau de n éléments (numérotés de 0 à n-1), le principe du tri par sélection est le suivant :
- rechercher le plus petit élément du tableau, et l’échanger avec l’élément d’indice 0 ;
- rechercher le second plus petit élément du tableau, et l’échanger avec l’élément d’indice 1 ;
- continuer de cette façon jusqu’à ce que le tableau soit entièrement trié.
En pseudo-code, l’algorithme s’écrit ainsi :

Dans tous les cas, pour trier n éléments, le tri par sélection effectue n(n-1)/2 comparaisons donc en O(n²).
Les tris itératifs : tri par insertion
Le tri par insertion est un algorithme de tri classique. La plupart des personnes l’utilisent naturellement pour trier des cartes à jouer.
Le tri par insertion considère chaque élément du tableau et l’insère à la bonne place parmi les éléments déjà triés. Ainsi, au moment où on considère un élément, les éléments qui le précèdent sont déjà triés, tandis que les éléments qui le suivent ne sont pas encore triés.
Pour trouver la place où insérer un élément parmi les précédents, il faut le comparer à ces derniers, et les décaler afin de libérer une place où effectuer l’insertion. Le décalage occupe la place laissée libre par l’élément considéré. En pratique, ces deux actions s’effectuent en une passe, qui consiste à faire « remonter » l’élément au fur et à mesure jusqu’à rencontrer un élément plus petit.
Voici un exemple pour mieux comprendre le principe sur le tableau [6, 5, 3, 1, 8, 7, 2, 4].

Voici son pseudo-code :

La complexité du tri par insertion est O(n²) dans le pire cas et linéaire dans le meilleur cas. Dans le pire cas, atteint lorsque le tableau est trié à l’envers, l’algorithme effectue de l’ordre de n²/2 affectations et comparaisons ; Si le tableau est déjà trié, il y a n-1 comparaisons et au plus n affectations.
Les tris itératifs : tri à bulles
Le tri à bulles ou tri par propagation est un algorithme de tri. Il consiste à comparer répétitivement les éléments consécutifs d’un tableau, et à les permuter lorsqu’ils sont mal triés. Il doit son nom au fait qu’il déplace rapidement les plus grands éléments en fin de tableau, comme des bulles d’air qui remonteraient rapidement à la surface d’un liquide.
L’algorithme parcourt le tableau et compare les éléments consécutifs. Lorsque deux éléments consécutifs ne sont pas dans l’ordre, ils sont permutés.
Après un premier parcours complet du tableau, le plus grand élément est forcément en fin de tableau, à sa position définitive. En effet, aussitôt que le plus grand élément est rencontré durant le parcours, il est mal trié par rapport à tous les éléments suivants, donc permuté avec le suivant jusqu’à arriver à la fin du parcours.
Après le premier parcours, le plus grand élément étant à sa position définitive, il n’a plus à être traité. Le reste du tableau est en revanche encore en désordre. Il faut donc le parcourir à nouveau, en s’arrêtant à l’avant-dernier élément. Après ce deuxième parcours, les deux plus grands éléments sont à leur position définitive. Il faut donc répéter les parcours du tableau, jusqu’à ce que les deux plus petits éléments soient placés à leur position définitive.
Une optimisation courante de ce tri consiste à l’interrompre dès qu’un parcours des éléments possiblement encore en désordre (boucle interne) est effectué sans permutation. En effet, cela signifie que tout le tableau est trié. Cette optimisation nécessite une variable supplémentaire.


Il est possible de mettre un Tant que à la place du premier Pour. Dans ce cas il faut incrémenté i dans l’intérieur de la boucle et plus besoin du break..
Pour le tri non optimisé, la complexité en temps est de O(n²), avec n la taille du tableau.
Pour le tri optimisé, le nombre d’itérations de la boucle externe est compris entre 1 et n. En effet, on peut démontrer qu’après la i-ème étape, les i derniers éléments du tableau sont à leur place. À chaque itération, il y a exactement n-1 comparaisons et au plus n-1 permutations.
Le pire cas (n itérations) est atteint lorsque le plus petit élément est à la fin du tableau. La complexité est alors O(n²). Le meilleur cas (une seule itération) est atteint quand le tableau est déjà trié. Dans ce cas, la complexité est linéaire.
Les tris itératifs : tri cocktail
Le tri cocktail ou tri shaker ou tri à bulles bidirectionnel est une variante du tri à bulles1 qui est à la fois un algorithme de tri et un tri par comparaison. La différence entre cet algorithme et le tri à bulles est qu’il exécute un tri dans chaque direction à chaque passe le long de la liste à trier.
Cet algorithme de tri n’est que légèrement plus difficile à comprendre et à mettre en œuvre que le tri à bulles, et il résout en partie le problème des tortues du tri à bulles (les tortues sont les petits éléments situés près de la fin de la liste d’origine, qui ne remontent que très lentement, un emplacement par itération, vers leur emplacement définitif).
Lors de la première passe, le premier parcours vers la droite déplace des éléments plus grands que leur voisin immédiat vers la droite, et, en particulier, va déplacer de proche en proche le plus grand élément de la liste à son emplacement définitif en fin de liste. Ensuite, le second parcours vers la gauche va déplacer les éléments plus petits que leur voisin immédiat vers la gauche, et, en particulier, déplacera l’élément le plus petit de la liste à son emplacement définitif en tête de liste. vers la gauche. De même, lors de la seconde passe, le second élément le plus grand et le second élément le plus petit rejoindront à leur tour leur emplacement définitif, et ainsi de suite.
Après i passes, les i premiers éléments et les i derniers éléments sont à leur emplacement définitif. Ils n’ont donc plus besoin d’être vérifiés. Il est donc possible d’optimiser cet algorithme en ne vérifiant à chaque passe que la partie centrale de la liste non encore triée définitivement. Ceci permet de réduire de moitié le nombre de comparaisons à effectuer.
Un dérivé du tri à bulles est le tri cocktail ou tri shaker. Cette méthode de tri est basée sur l’observation suivante : dans le tri à bulles, les éléments peuvent avancer rapidement vers la fin du tableau, mais ne sont déplacés vers le début du tableau que d’une position à la fois.
L’idée du tri cocktail consiste à alterner le sens du parcours. On obtient un tri un peu plus rapide, d’une part parce qu’il nécessite moins de comparaisons, d’autre part parce qu’il relit les données les plus récentes lors du changement de sens (elles sont donc encore dans la mémoire cache). Cependant, le nombre de permutations à effectuer est identique. Ainsi, le temps d’exécution est toujours proportionnel à n² donc médiocre.

La complexité au pire et au mieux en O(.) est la même que le tri à bulle.
Les tris récursifs : tri rapide
Le tri rapide (quicksort en anglais) est un algorithme de tri par comparaison, son fonctionnement est plutôt simple à comprendre et il est très utilisé sur de grandes entrées. En effet, il a pour complexité moyenne O(NlogN) et O(N²) dans le pire des cas.
Le tri rapide utilise le principe de diviser pour régner, c’est-à-dire que l’on va choisir un élément du tableau (qu’on appelle pivot), puis l’on réorganise le tableau initial en deux sous tableaux :
- L’un contenant les éléments inférieurs au pivot.
- L’autre contenant les éléments supérieurs au pivot.
On continue ce procédé (qu’on appelle partitionnement, c’est-à-dire choisir un pivot et réorganiser le tableau) jusqu’à se retrouver avec un tableau découpé en N sous tableaux (N étant la taille du tableau), qui est donc trié.
Prenons 5, 9, 7, 3, 8 comme suite de nombres, et trions la dans l’ordre croissant avec l’algorithme du tri rapide :
5, 9, 7, 3, 8 -> on choisit le pivot, dans notre cas je choisis l’élément du milieu, 7.
5, 3 | 7 | 9, 8 -> on découpe le tableau en trois parties, une partie avec des éléments inférieurs au pivot (5 et 3), la partie contenant le pivot (7), et une partie avec les éléments supérieurs au pivot (9 et 8). On peut déjà dire qu’on a placé le pivot à sa place définitive dans le tableau, puisque les autres éléments sont soit supérieurs soit inférieurs à lui.
5, 3 | 7 | 9, 8 -> on recommence en choisissant de nouveau un pivot pour chaque sous tableaux créés.
3 | 5 | 7 | 8 | 9 -> dernière étape du partitionnement, désormais aucuns sous tableaux ne contient plus d’un élément, le tri est donc terminé.

Les tris récursifs : tri fusion
Le tri par fusion est l’un des algorithmes de tri les plus populaires et les plus efficaces. Et il est basé sur le paradigme Diviser pour régner.

Supposons que nous devions trier un tableau T. Un sous-problème serait de trier une sous-section (sous-tableau) de ce tableau commençant à l’indice debut et se terminant à l’indice fin, notée T[debut..fin].
Si milieu est le point milieu entre debut et fin, alors nous pouvons diviser le sous-tableau T[debut..fin] en deux tableaux T[debut..milieu] et T[milieu + 1, fin]. Dans l’étape Régner, nous essayons de trier les sous-réseaux T[debut..milieu] et T[milieu + 1, fin]. Si nous n’avons pas encore atteint le cas de base (le sous-tableau contient un seul élément), nous divisons à nouveau ces deux sous-réseaux et essayons de les trier.
Lorsque l’étape de conquête atteint l’étape de base et que nous obtenons deux sous-tableaux triés T[debut..milieu] et T[milieu + 1, fin] pour le tableau T[debut..milieu], nous combinons les résultats en créant un tableau trié T[debut..milieu] à partir de deux sous-réseaux triés T[debut..milieu] et T[milieu + 1, fin].
La fonction triFusion divise à plusieurs reprises le tableau en deux moitiés (deux sous-tableaux) jusqu’à ce que nous atteignions un stade où nous essayons d’effectuer triFusion sur un sous-tableau de taille 1, c’est-à-dire debut == fin.
Après cela, la fonction de fusion entre en jeu et combine les tableaux triés dans un tableau plus grand jusqu’à ce que l’ensemble du tableau soit fusionné. Après cela, la fonction de fusion récupère les sous-tableaux triés et les fusionne pour trier progressivement l’ensemble du tableau.
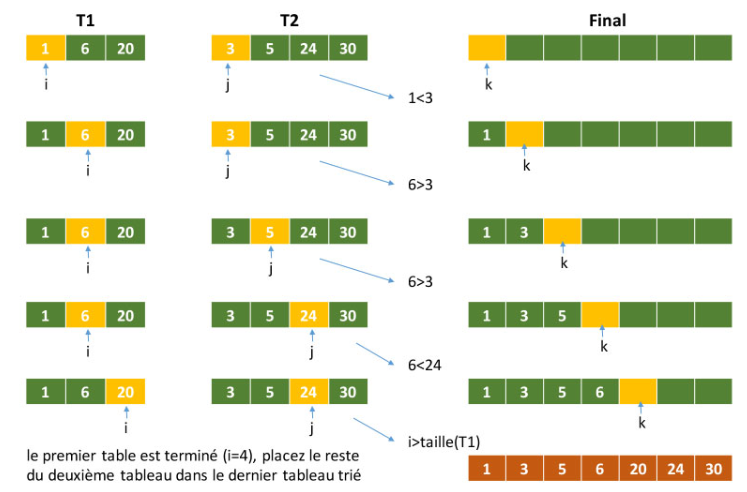
La complexité temporelle du tri par fusion est O(nLogn) dans les 3 cas (pire, moyen et meilleur) car le tri par fusion divise toujours le tableau en deux moitiés et prend un temps linéaire pour fusionner deux moitiés.
Ce pseudo-code est très simplifié :
- Dans la fonction triFusion, on utilise la récursivité pour découper puis fusionner notre tableau, et on arrête les appels récursifs lorsque le sous tableau que l’on traite n’a plus qu’un seul élément.
- La fonction fusionner est assez explicite, elle nous permet de créer à partir de deux sous tableaux triés, un tableau lui aussi trié en temps linéaire.


