Contenus
ToggleExercices corrigés sous le logiciel LARP
Les exercices corrigés suivants concernent la création d’algorithme selon la structure logigramme du logiciel LARP.

Pour bien débuter
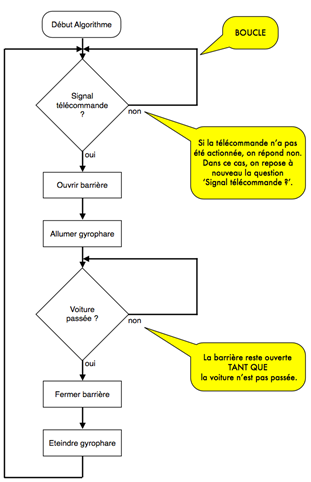
Rédige le logigramme permettant le fonctionnement suivant :
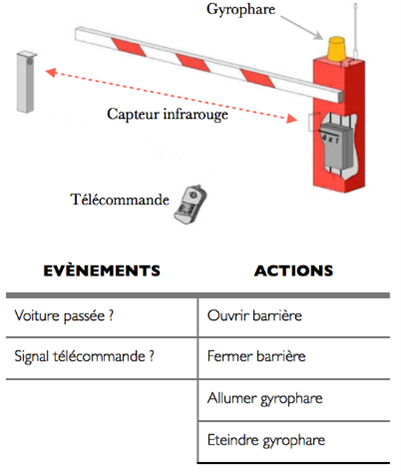
- Une barrière s’ouvre à l’aide d’une télécommande à distance.
- Le système utilise un capteur infrarouge pour savoir si la voiture est passée.
- La barrière se referme quand la voiture est passée
- Un gyrophare s’allume lorsque la barrière est ouverte et s’éteint lorsque la barrière est fermée.
Utilise uniquement les actions et événements indiqués ci-dessous :
Exercice 1
Défi 1: trouver le centre d’un cercle. Rédiger l’organigramme des opérations permettant de trouver le centre d’un cercle. Il n’est pas interdit de donner un nom à votre algorithme.
Défi 2 : Diviser un cercle en 6 parties égales. Rédiger l’organigramme des opérations permettant diviser un cercle en 6 parties égales. Il n’est pas interdit de d’utiliser un algorithme existant s’il a un nom; On peut alors l’appeler par son nom : Exécuter « monAlgo ».
Défi 1 :
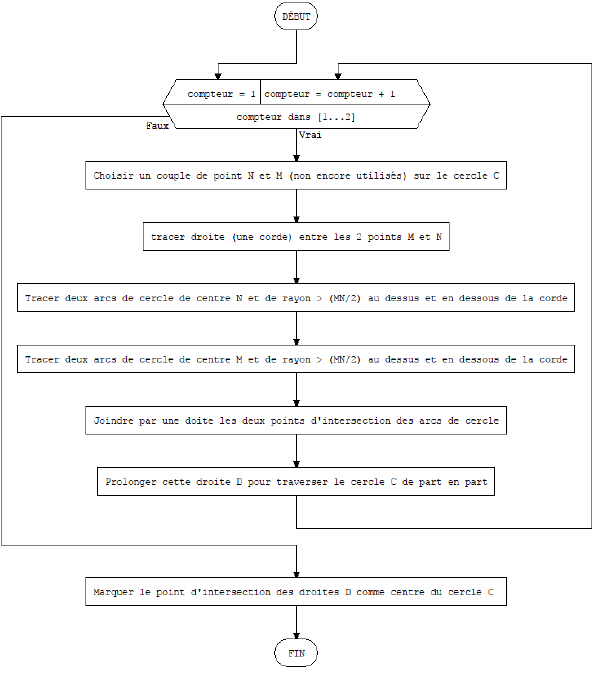
Défi 2 :

Exercice 2
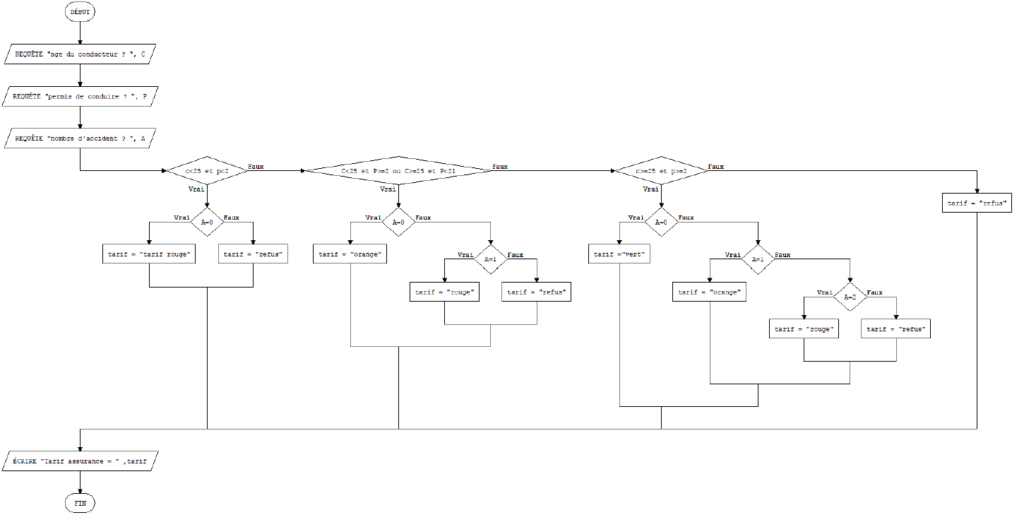
Une compagnie d’assurance propose à ses clients quatre tarifs identifiables par une couleur, du moins au plus onéreux : blanc, vert, orange, rouge.
Le tarif dépend de la situation du conducteur :
- Un conducteur de moins de 25 ans et titulaire du permis depuis moins de deux ans, se voit attribuer le tarif rouge, si toutefois il n’a jamais été responsable d’accident. Sinon, la compagnie refuse de l’assurer.
- Un conducteur de moins de 25 ans et titulaire du permis depuis plus de deux ans, ou de plus de 25 ans mais titulaire du permis depuis moins de deux ans a le droit au tarif orange s’il n’a jamais provoqué d’accident, au tarif rouge pour un accident, sinon il est refusé.
- Un conducteur de plus de 25 ans titulaire du permis depuis plus de deux ans bénéficie du tarif vert s’il n’est à l’origine d’aucun accident et du tarif orange pour un accident, du tarif rouge pour deux accidents, et refusé au-delà.
Exercice 3
Etablir le pseudo-code de l’algorithme répondant au besoin suivant :
L’algorithme commence par vous demander le montant de l’emprunt initial (à taux zéro).
Puis il enregistre le montant de vos remboursements successifs.
A chaque remboursement l’algorithme vous renvoi une information: le montant du capital restant à rembourser.
DÉBUT
REQUÊTE « montant emprunt ? « , E
TANTQUE E>0 FAIRE
REQUÊTE « montant remboursement ? » ,R
SI (E-R >=0) ALORS
E = E-R
ÉCRIRE « montant restant à remourser => « , E
SINON
ÉCRIRE « votre remboursement est trop élevé »
ÉCRIRE « valeur maximale => « , E
FINSI
FINTANTQUE
ÉCRIRE « fin du remboursement «
FIN
Exercice 4
Défi 1 : Ecrire l’organigramme d’un algorithme qui demande à l’utilisateur un nombre puis qui affiche sa valeur absolue. L’essayer avec des nombres positifs et négatifs (traiter le cas de la valeur 0)
Défi 2 : Ecrire le pseudo-code d’un algorithme qui demande à l’utilisateur deux nombres différents puis qui affiche le plus grand. L’essayer avec des couples de nombres couvrant tous les cas possibles.
Défi 3 : Ecrire l’organigramme d’un algorithme qui demande à l’utilisateur 4 nombres entiers a, b, c, d. L’algorithme doit donner la solution de l’équation ax + b = cx + d. Ou informer l’utilisateur des situations particulières de résolution de l’équation. Tester l’algorithme dans les divers cas possibles.
Défi 4 : Ecrire le pseudo-code d’un algorithme qui demande à l’utilisateur 3 nombres entiers a, b, c. L’algorithme doit donner la ou les solutions réelles de l’équation ax2 + bx + c = 0. Tester dans les diverses situations possibles.
Défi 5 : Ecrire le pseudo-code d’un algorithme qui affiche la liste des carrés des nombres tant que le carré est inférieur à 100
Défi 6 : Ecrire le pseudo-code d’un algorithme qui affiche la liste des nombres entiers multiples de 3
Défi 7 : Ecrire le pseudo-code d’un algorithme qui affiche la liste des nombres entiers multiples de 3 et de 5
Défi 1 :
DÉBUT
REQUÊTE « saisissez un nombre ? » , N
SI N>0 ALORS
val_abs = N
SINON
val_abs = -N
FINSI
ECRIRE « la valeur absolue de « , N , » est « , val_abs
FIN
Défi 2 :
DÉBUT
REQUÊTE « un premier nombre ? » , N1
REQUÊTE « un deuxième nombre ? » , N2
SI N1>N2 ALORS
ECRIRE N1, » est plus grand que « ,N2
SINON
ECRIRE N2, » est plus grand que « ,N1
FINSI
FIN
Défi 4 :
DÉBUT
REQUÊTE « saisir le coefficient a > « , a
REQUÊTE « saisir le coefficient b > « , b
REQUÊTE « saisir le coefficient c > « , c
d = b*b – 4*a*c
SI d >0 ALORS
R1 = (-b + RACINE(d)) / (2*a)
R2 = (-b + RACINE(d)) / (2*a)
ÉCRIRE » il y a deux racines : « , R1, » et « , R2
SINON SI d=0 ALORS
R = (-b) / (2*a)
ÉCRIRE » il y a une seule racine : « , R
SINON SI d <0 ALORS
ÉCRIRE » il n’y a pas de racine réelle »
FINSI
FIN
Défi 5 :
DÉBUT
nombre =1
TANTQUE (nombre * nombre <100) FAIRE
ÉCRIRE nombre , » « , nombre*nombre
nombre = nombre + 1
FINTANTQUE
FIN
Exercice 5
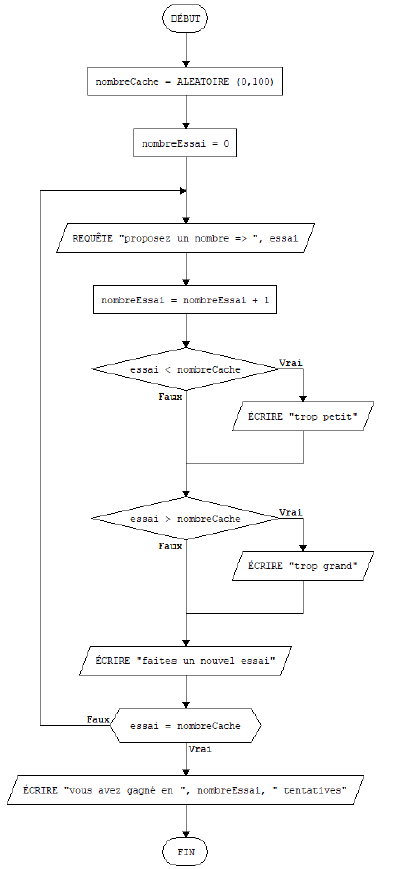
L’ordinateur choisit un nombre mystère compris ente 1 et 100. Et vous devrez le retrouver.
Pour permettre à l’ordinateur de disposer d’un nombre aléatoire compris entre deux valeurs entières et faire ainsi une proposition de réponse, vous pouvez utiliser la fonction suivante :
nombre = ALEATOIRE (p , q) pour obtenir un nombre aléatoire dans l’intervalle [p , q]
Etablir à votre choix l’organigramme ou le pseudo code (ou les deux…) d’un algorithme qui permet à l’ordinateur de répondre à vos proposition de nombre
Message « trop petit » si votre nombre est plus petit que le nombre mystère
Message « trop grand » si votre nombre est plus grand que le nombre mystère
Message « gagné » si votre nombre est le nombre mystère
Testez vos algorithmes.
Exercice 6
Défi 1 : Rédiger l’organigramme d’un programme qui
- Demande des notes (nombre de notes inconnu)
- Les rangent dans un conteneur
Le programme s’arrête de demander des notes quand il reçoit une note négative.
Ensuite
- Il calcule la moyenne des notes
- Il affiche le nombre de notes saisies et la moyenne de ces notes
Rédiger l’organigramme, l’essayer, puis le traduire en pseudo code
Défi 2 : Pour obtenir des valeurs d’entiers aléatoires utiliser la fonction ALEATOIRE (p) qui fournit un entier aléatoire dans l’intervalle ]0 , p].
Valeur = ALEATOIRE (p)
Une fois le conteneur rempli, le programme affichera le contenu du conteneur : position et valeur
Défi 3 : Rédiger en pseudo-code un programme qui
- Remplit un conteneur de valeur aléatoire (cf défi 2)
- Recherche la plus petite valeur du conteneur
- Affiche le message « la plus petite valeur est » et la valeur trouvée
Défi 4 : Rédiger l’algorithme du calcul de factorielle n! Choisir la représentation de votre choix et essayez votre algorithme avec des valeurs variées (1, 3,6, 12, 0,-4)
Défi 5 : PGCD de a et b par l’algorithme d’Euclide
- Demander les deux nombres a et b
- Exécuter la division euclidienne de a par b ; on note r le résultat de cette division
- a prend la valeur de b et b prend la valeur de r
- on recommence en 2
- quand la décision donne un reste égal à 0 le PGCD est le dernier reste non nul
- Afficher alors le PGCD
Rédigez votre algorithme et testez le pour divers couples de valeurs (a,b)
Question : que ce passe t’il si le reste d’une division est 1 ?
Corrigez et adaptez votre algorithme pour tenir compte de ce cas
Défi 6 : Vérifier la conjecture de Syracuse
- Prendre un nombre entier
- Si ce nombre est pair, le diviser par 2
- Si ce nombre est impair, prendre le triple et ajouter 1
- On obtient un nouveau nombre entier et on recommence à 2.
A la fin on obtient toujours 1.
Rédigez cet algorithme et obtenez qu’à la fin (quand on obtient 1) il affiche le nombre d’itérations effectuées.
Défi 7 : Calculer par encadrement une valeur approchée à 10-6 du nombre d’or. En utilisant la formule : La valeur entre deux valeurs successives du calcul du nombre d’or doit être inférieure à 10
Défi 9 : Vérifier si un nombre entier demandé par l’algorithme est premier ou non. L’algorithme doit répondre : le nombre est premier ou le nombre n’est pas premier. Une piste : un nombre n est premier s’il a exactement 2 diviseurs dans l’intervalle [1 , n]
Défi 10 : Vérifier si un nombre entier demandé par l’algorithme est premier ou non. L’algorithme doit répondre : le nombre est premier ou le nombre n’est pas premier. Même question mais trouver une autre approche pour un autre algorithme. Une piste : un nombre n est premier s’il existe un diviseur pour ce nombre dans l’intervalle ]1 , n[
Défi 11 : réflexion sur les algorithmes de nombre premier
Selon vous lequel de ces deux algorithmes est le plus efficace et pourquoi ?
Défi 4 :
ENTRER n
facto = 1
SI (n!=0)ALORS
POUR compteur = 1 JUSQU’À n FAIRE
facto = facto*compteur
FINPOUR
SINON
facto = 1
FINSI
RETOURNER facto
Défi 5 :

Défi 6 :
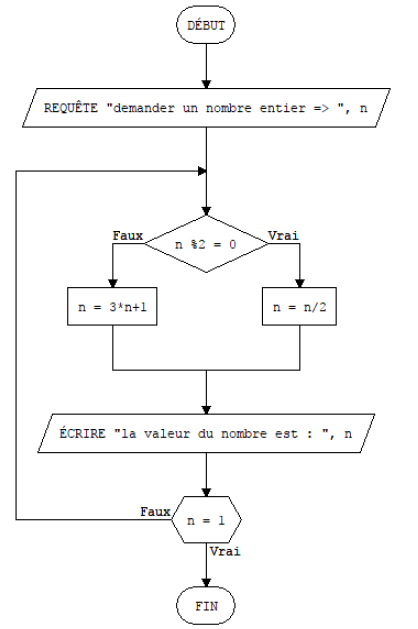
Défi 9 :
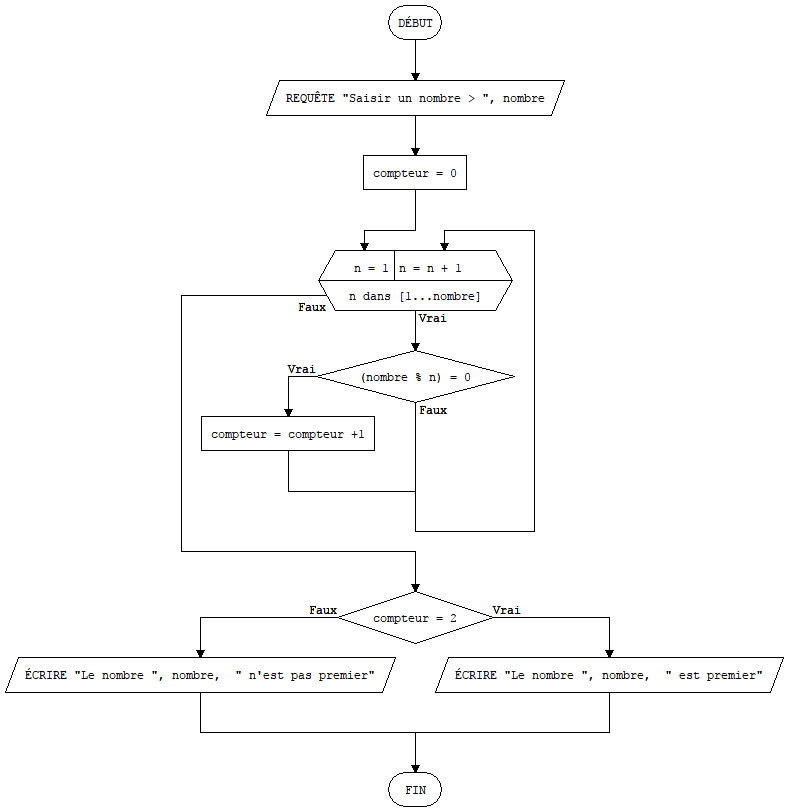
Défi 10 :
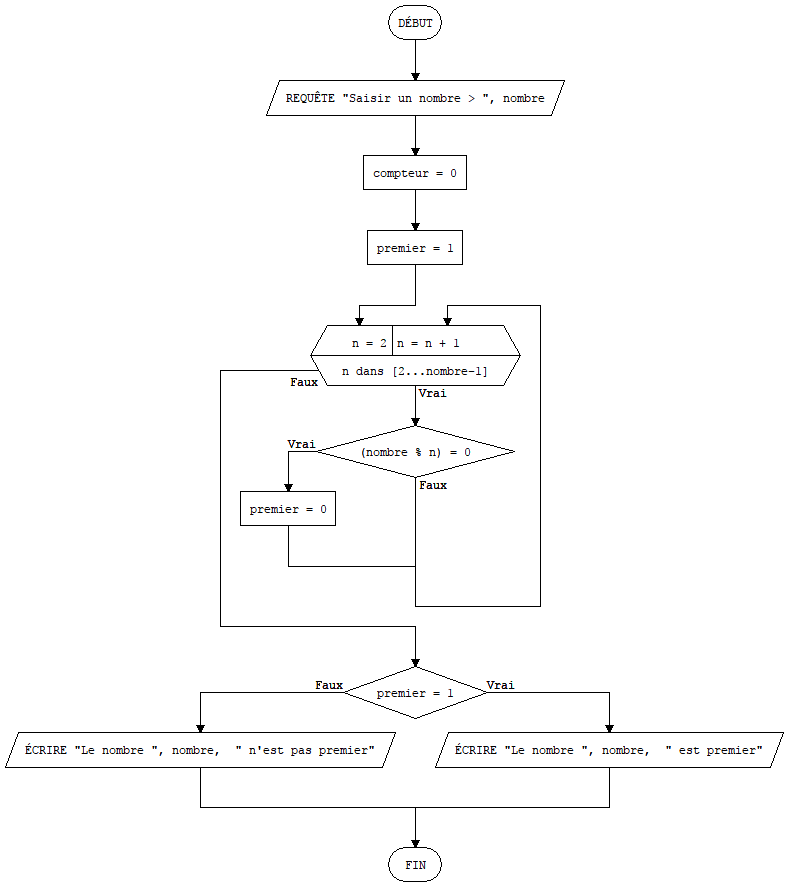
Exercice 7
Une étude menée par un institut de sondage a montré que depuis 2001.
5% des adhérents d’un parti A quittent ce parti pour le parti B.
8% des adhérents du parti B quittent ce parti pour le parti A.
En 2001 le parti A compatit 40 000 adhérents et le parti B en comptait 70 000.
Etablir l’organigramme d’un algorithme qui permettra de déterminer en quelle année le nombre d’adhérent du parti B dépassera celui du parti A.
Exercice 8
Défi 1 : Etablir l’organigramme d’un algorithme qui demande des coordonnées polaires et effectue la conversion en coordonnées cartésiennes. On se limitera à des coordonnée planes, mais si cela vous tente, … pourquoi pas en 3D.
Défi 2 : Etablir l’organigramme d’un algorithme qui demande des coordonnées cartésiennes et effectue la conversion en coordonnées polaires. Idem pour la 3D.
Défi 3 : Rédiger l’organigramme d’un programme qui
Demande quel type de conversion on souhaite effectuer (P vers C ou C vers P)
Exécute l’organigramme du défi 1 o u2 selon la réponse à la question initiale.
Défi 4 : Compléter l’organigramme précédent pour que l’exécution de l’algorithme demande après que la conversion ait été effectué, si l’on veut recommencer et recommence tant que la réponse est oui.
Défi 5 : En arithmétique, un nombre parfait est un entier naturel n tel que σ(n) = 2n où σ(n) est la somme des diviseurs positifs de n. Cela revient à dire qu’un entier naturel est parfait s’il est égal à la moitié de la somme de ses diviseurs ou encore à la somme de ses diviseurs stricts. Ainsi 6 est un nombre parfait car 2 × 6 = 12 = 1 + 2 + 3 + 6, ou encore 6 = 1 + 2 + 3
Rédiger l’organigramme d’un programme qui
Recherche et affiche les nombres premiers à partir de 1 inclus.
Pour information :
Il y a 4 nombres parfaits entre (1 et 10 000) connus de puis l’antiquité (Euclide)
Puis : 33 550 336, puis…. 2 305 843 008 139 952 128 (découvert par Leonhard Euler), puis d’autres. En tout aujourd’hui 49 dont le dernier découvert En janvier 2016.
Défi 6 : Rédiger en pseudo code, un programme qui
Effectue la somme des entiers : ∑ n pour n valant 1 jusqu’à + ∞
Affiche pour chaque valeur de n la valeur de la somme obtenue
Tester votre programme pour une valeur de n aussi grande que possible. La capacité de traitement votre ordinateur devrait vous limiter.
Evaluer la limite de cette somme pour n tendant vers + ∞ et vérifier la sommation de Ramanujan :
1 + 2 + 3 + 4 + 5 +…..à l’infini = -1/12.
Défi 7 : Rédiger en pseudo-code un algorithme qui
Calcul une valeur approchée de √150 à la 5ème décimale (x n+1-x n <10-5)
Utiliser le formule xn+1 = (x n+a/x n)/2
Défi 8 : Rédiger en pseudo-code un algorithme qui
Demande la valeur d’un placement initial puis calcule et affiche année après année l’évolution de capital à un taux de 3% par an
Le placement initial est effectué en début d’année (au 1er janvier)
L’évaluation du capital et le versement des intérêts se fait en fin d’année (le 31 décembre)
Défi 9 : Rédiger en pseudo-code un algorithme qui
Détermine la dernière valeur n des puissances de 2n telle que 2n <10 000
Défi 5 :

Ce qui donne l’algorithme suivant :

Défi 7 :
DÉBUT
REQUÊTE « valeur de a = « , nombre
Un = nombre
precision = 0.00001
compteur = 0
RÉPÉTER
U = Un
Un = (U+nombre/U)/2.0
ecart = ABSOLU(Un-U)
compteur = compteur +1
JUSQU’À (ecart < precision)
ÉCRIRE « la racine de « ,nombre, » est « ,ARRONDIR(Un)
ÉCRIRE « resultat obtenu en « ,compteur , »tours de boucle »
FIN
Défi 8 :
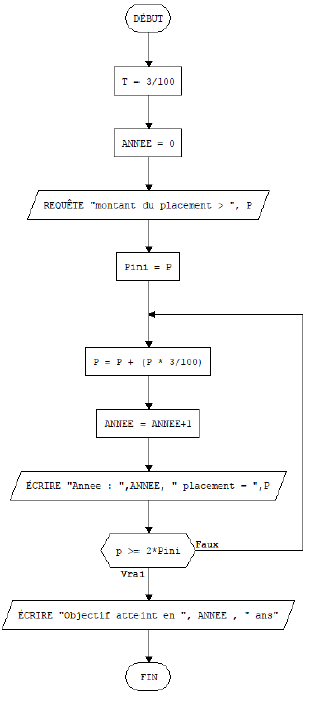
DÉBUT
T = 3/100
ANNEE = 0
REQUÊTE « montant du placement > « , P
Pini = P
RÉPÉTER
P = P + (P * 3/100)
ANNEE = ANNEE+1
ÉCRIRE « Annee : « ,ANNEE, » placement = « ,P
JUSQU’À p >= 2*Pini
ÉCRIRE « Objectif atteint en « , ANNEE , » ans »
FIN
Exercice 9
On étale un ensemble d’allumettes (par exemple 17), chaque joueur retire à son tour de jeu de 1 à 3 allumettes. Le gagnant est celui retire la dernière allumette (jeu de Nim).
La stratégie gagnante est de laisser à votre adversaire un nombre d’allumettes égal à 1modulo 4.
Rédiger l’organigramme de l’algorithme du jeu dans lequel
- L’ordinateur demande le nombre d’allumettes du jeu
- Fait jouer le joueur humain
- Joue à son tour en supprimant
- Le nombre d’allumettes nécessaire pour en laisser 1 modulo 4 si cela est possible
- Un nombre aléatoire entre 1 et 3 sinon
- Et ainsi de suite jusqu’à ce qu’il ne reste plus qu’une allumette
- Le programme désigne alors le gagnant
Pour permettre à l’ordinateur de disposer d’un nombre aléatoire compris entre deux valeurs entières et faire ainsi une proposition de réponse, vous pouvez utiliser la fonction suivante :
nombre = ALEATOIRE (p,q) pour obtenir un nombre aléatoire dans l’intervalle [p , q]
EN CONSTRUCTION