Programmation récursive

Contenus

La programmation récursive est une technique de programmation remplaçant les instructions de boucle par des appels de fonctions. Le mécanisme consiste donc, dans la grande majorité des cas, à créer une fonction qui s’appelle elle-même une ou plusieurs fois selon différents critères.

La structure d’un algorithme récursif est la suivant :

 algo ()
{
   condition 1
   condition 2
   ...
   condition n
}

Les conditions sont généralement des if, ils incluent les conditions d’arrêts (ne retourne pas la fonction) ou des conditions de continuité (relance la fonction ou retourne la fonction). Les conditions de continuité modifient les entrées de la fonction relancée. Une fonction récursive possède obligatoirement au moins une condition d’arrêt.

Récursivité simple

Une fonction simplement récursive s’appelle elle-même une seule fois au plus dans chaque condition.

Le programme mathématique est du type suivant (exemple pour le calcul d’une puissance) :

programmation récursive récursion terminal algorithmique puissance

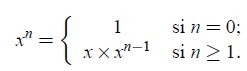
Voici un exemple simple permettant de calculer la factorielle de n :

 int fact(n)
{
   if (n==0) return 1;
   else return n*fact(n-1);
}

Ici, nous voyons bien le fait que la récursivité se comporte comme une boucle.

Récursivité multiple

Une fonction récursive multiple peut s’appeler elle-même plusieurs fois dans chaque condition.

Le programme mathématique est du type suivant (exemple pour la relation de Pascal) :

programmation récursive récursion terminal algorithmique récursivité multiple pascal

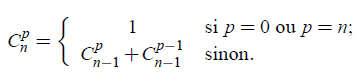
Donnera pour programme :

 int pascal(n, p)
{
   if (p==0 || p==n) return 1;
   else return pascal(p, n-1)+pascal(p-1,n-1);
}

Autres types

Deux algorithmes sont « mutuellement » récursifs si l’un fait appel à l’autre et réciproquement.

Un algorithme contient une récursivité « imbriquée » s’il un paramètre de la récursion est un appel à lui-même.

Pile d’exécution

La pile d’exécution du programme en cours est un emplacement mémoire destiné à mémoriser les paramètres, les variables locales ainsi que les adresses de retour des fonctions en cours d’exécution.

Cette pile fonctionne selon le principe des LIFO (last in first out) et possède une taille fixée. Voici la pile pour la factorielle simple, dès que le programme lit une méthode, il l’exécute en retenant le reste des informations dans la pile, et il ajoute les nouveaux résultats en haut de la pile. Puisqu’elle est LIFO, cette dernière information sera ensuite lue en premier, c’est pourquoi cela donne une impression de pyramide d’exécution :

Appel à fact(3)
   3*fact(2)
   Appel à fact(2)
      2*fact(1)
      Appel à fact(1)
         1*fact(0)
         Appel à fact(0)
            Retourne la valeur 1
         Retourne 1*1
      Retourne 2*1
   Retourne 3*2
Retourne 6

La pile d’exécution de la suite de Fibonacci suit le même principe :

int fibo(n)
{
   return (n<2) ? 1 : fibo(n-1)+fibo(n-2);
}

Fibo(3)
   Fibo(2)+attente
   Appel à Fibo(2)
      Fibo(1)+attente
      Appel à Fibo(1)
         Retourne 1
      1+Fibo(0)
      Appel à Fibo(0)
         Retourne 1
      Retourne 1+1
   2+Fibo(1)
   Appel à Fibo(1)
      Retourne 1
   Retourne 2+1
Retourne 3

Nous voyons bien ici un effet de montagnes russes dû au dépilement successif de la fonction à gauche dès qu’elle est rencontrée. Il est plus facile de représenter la pile d’une fonction récursive multiple par un parcours en profondeur (on va le plus loin dans les successeurs) de l’arbre de ses appels récursif :

programmation récursive récursion terminal algorithmique récursivité multiple arbre d'appel Fibonacci

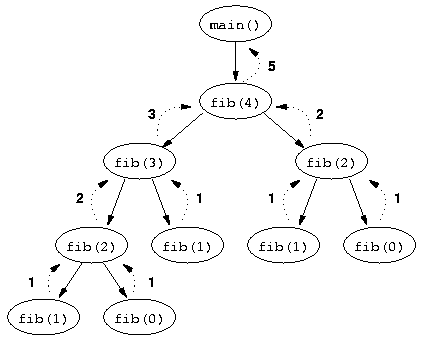
Récursivité terminale

On dit qu’une fonction est récursive terminale si le résultat de cet appel est le résultat de la fonction.

Ainsi, la pile n’a rien en mémoire tout au long de la récursivité. Cela signifie que la valeur retournée est directement la valeur obtenue sans qu’il n’y ait aucune opération supplémentaire. Reprenons l’exemple de la factorielle de façon récursive terminale :

 int fact(n,a)
{
   if (n==0) return a;
   else return fact (n-1, n*a);
} // attention, la valeur de a au départ est très importante

Cela revient exactement à écrire la boucle suivante :

 while (n != 0
{
   n*=a;
   n--;
}