La mesure d’impureté (de Gini) implémente des arbres de décision binaires et les trois mesures d’impuretés ou critères de division couramment utilisés dans les arbres de décision binaires sont l’impureté de Gini (IG), l’entropie (IH) et l’erreur de classification (IE).

Contenus
ToggleImpureté de Gini
Utilisée par l’algorithme CART (arbre de classification et de régression) pour les arbres de classification, l’impureté Gini est une mesure de la fréquence à laquelle un élément choisi au hasard dans l’ensemble serait incorrectement étiqueté s’il était étiqueté de manière aléatoire en fonction de la distribution des étiquettes dans le sous-ensemble.
Mathématiquement, nous pouvons écrire l’impureté de Gini comme suit :
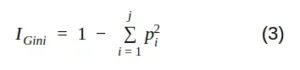
où j est le nombre de classes présentes dans le nœud et p est la distribution de la classe dans le nœud.
Simulation simple avec un ensemble de données sur les maladies cardiaques comprenant 303 lignes et 13 attributs. La cible comprend 138 valeurs 0 et 165 valeurs 1
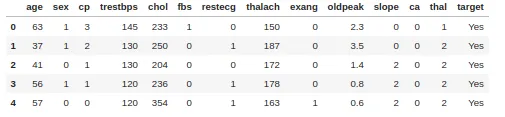
Afin de créer un arbre de décision à partir de l’ensemble de données et de déterminer quelle séparation est la meilleure, nous avons besoin d’un moyen de mesurer et de comparer l’impureté dans chaque attribut. La valeur d’impureté la plus basse lors de la première itération sera le nœud racine. on peut écrire l’équation 3 sous la forme :
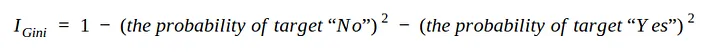
Dans cette simulation, utilisez uniquement les attributs sexe, fbs (glycémie à jeun), exang (angor induit par l’exercice) et cible.
Comment mesurer l’impureté dans l’attribut Sexe :

- Noeud gauche = 0.29
- Noeud droite = 0.49
Maintenant que nous avons mesuré l’impureté pour les deux nœuds feuilles. Nous pouvons calculer l’impureté totale avec la moyenne pondérale. Le nœud gauche représentait 138 patients tandis que le nœud droit représentait 165 patients.
Impureté totale de Gini — Nœud feuille

On procède de même avec les autres attributs :
- I_fbs_left = 0.268; droite = 0.234; I_fbs = 0.249
- I_exang_left =0.596; droite = 0.234; I_Exang = 0.399
Fbs (glycémie à jeun) a l’impureté Gini la plus faible, alors utilisez-le au niveau du nœud racine.
Impureté de Gini en données quantitatives
Comme le poids qui est l’un des attributs permettant de déterminer les maladies cardiaques, par exemple nous avons l’attribut poids :

Après avoir ordonné par ordre croissant, faites la moyenne par pair consécutive et calculer l’impureté pour chaque valeur.
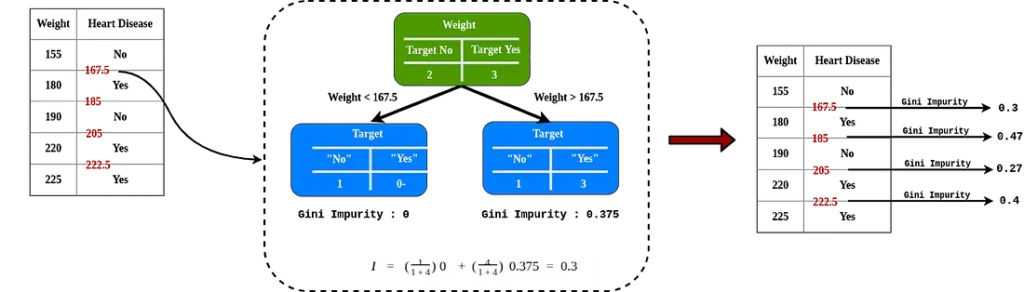
L’impureté Gini la plus basse est un poids < 205, il s’agit de la valeur seuil et de la valeur de l’impureté si elle est utilisée lorsque nous comparons avec un autre attribut.
Pour des soucis de calcul, il est aussi possible de faire par quantile.
Impureté de Gini en données qualitative
Nous avons un attribut de couleur préféré pour déterminer le sexe d’une personne :

Afin de connaître l’impureté cet attribut, calculez un score d’impureté pour chacun (en tant que valeur booléenne) ainsi que chaque combinaison possible.
Entropie
Utilisé par les algorithmes de génération d’arborescence ID3, C4.5 et C5.0. Le gain d’information est basé sur la notion d’entropie, la mesure de l’entropie est définie comme :
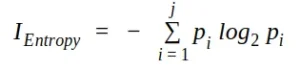
où j est le nombre de classes présentes dans le nœud et p est la distribution de la classe dans le nœud.
Dans le même cas et le même ensemble de données, nous avons besoin d’un moyen de mesurer et de comparer l’entropie dans chaque attribut. La valeur d’entropie la plus élevée lors de la première itération sera le nœud racine.
Nous devons d’abord calculer l’entropie dans l’attribut Target = 0.994.
On utilise le même split pour sex :
- sex = 0 a pour entropie 0.666
- sex = 1 a pour entropie 0.988
Maintenant que nous avons mesuré l’entropie pour les deux nœuds feuilles. Nous reprenons la moyenne des poids pour calculer la valeur d’entropie totale.

Entropie pour la colonne Fbs = 0.389
Entropie pour la colonne Exang = 0.224
Fbs (glycémie à jeun) a l’entropie la plus élevée, nous l’utiliserons donc au niveau du nœud racine, exactement les mêmes résultats que nous avons obtenus avec l’impureté Gini.
Erreur de classification / Misclassification impurity
Une autre mesure d’impureté est l’impureté de classification erronée ou erreur de classification. Mathématiquement, nous pouvons écrire l’impureté de classification erronée comme suit :
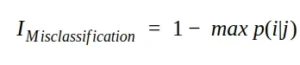
En termes de performances qualitatives, cet indice n’est pas le meilleur choix car il n’est pas particulièrement sensible aux différentes distributions de probabilité (qui peuvent facilement conduire la sélection vers une subdivision en utilisant Gini ou l’entropie).
