Après avoir réalisé une analyse descriptive des données, rempli les vides et sélectionner les premières colonnes. Il est important de continuer de réduire les dimensions, pour cela, ce tutoriel sur le t-SNE présente la réduction de dimensions par analyse non-linéaire.

Contenus
ToggleTutoriel sur le t-SNE et réduction de dimensions non-linéaire
La plupart des ensembles de données du monde réel ont de nombreuses fonctionnalités, parfois plusieurs milliers. Chacun d’eux peut être considéré comme une dimension dans l’espace des points de données. Par conséquent, le plus souvent, nous traitons des ensembles de données de grande dimension, où la visualisation complète est assez difficile.
Pour examiner un ensemble de données dans son ensemble, nous devons réduire le nombre de dimensions utilisées dans la visualisation sans perdre beaucoup d’informations sur les données. Cette tâche est appelée réduction de dimensionnalité et est un exemple de problème d’apprentissage non supervisé car nous devons dériver de nouvelles caractéristiques de faible dimension à partir des données elles-mêmes, sans aucune entrée supervisée.
L’une des méthodes bien connues de réduction de la dimensionnalité est l’analyse en composantes principales (ACP), que nous étudierons plus loin dans ce cours. Sa limitation est qu’il s’agit d’un algorithme linéaire qui implique certaines restrictions sur les données.
Il existe également de nombreuses méthodes non linéaires, appelées collectivement Manifold Learning. L’un des plus connus d’entre eux est le t-SNE, d’où ce tutoriel sur le t-SNE 🙂
Le nom de la méthode semble complexe et un peu intimidant : t-distributed Stohastic Neighbor Embedding. Ses mathématiques sont également impressionnantes (nous ne nous y attarderons pas ici, mais, si vous vous sentez courageux, voici l’article original de Laurens van der Maaten et Geoffrey Hinton de JMLR).
Son idée de base est simple : trouver une projection pour un espace de caractéristiques de grande dimension sur un plan (ou un hyperplan 3D, mais il est presque toujours 2D) de telle sorte que les points qui étaient éloignés dans l’espace initial à n dimensions se termineront loin l’un de l’autre dans le plan. Ceux qui étaient proches à l’origine resteront proches les uns des autres.
Essentiellement, l’incorporation de voisins est une recherche d’une représentation de données nouvelle et moins dimensionnelle qui préserve le voisinage des exemples.
Représentation du t-SNE
Maintenant, pratiquons un peu. Tout d’abord, nous devons importer des classes supplémentaires :
from sklearn.manifold import TSNE
from sklearn.preprocessing import StandardScalerNous laisserons de côté les fonctionnalités State et Churn et convertirons les valeurs « Oui »/ »Non » des fonctionnalités binaires en valeurs numériques à l’aide de pandas.Series.map() :
X = df.drop(['Churn', 'State'], axis=1)
X['International plan'] = X['International plan'].
map({'Yes': 1, 'No': 0})
X['Voice mail plan'] = X['Voice mail plan'].
map({'Yes': 1, 'No': 0})Nous devons également normaliser les données. Pour cela, nous allons soustraire la moyenne de chaque variable et la diviser par son écart-type. Tout cela peut être fait avec StandardScaler.
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)Construisons maintenant une représentation t-SNE :
%%time tsne = TSNE(random_state=17)
tsne_repr = tsne.fit_transform(X_scaled)CPU times: user 1min 32s, sys: 7.86 s, total: 1min 39s
Wall time: 1min 39s
Colorons cette représentation t-SNE en fonction du churn (vert pour les clients fidèles, et rouge pour ceux qui sont partis).
plt.scatter(tsne_repr[:, 0], tsne_repr[:, 1],
c=df['Churn'].map({False: 'green', True: 'red'}));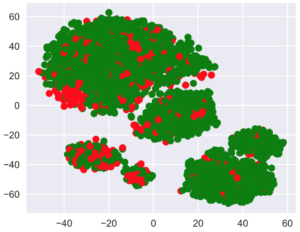
Nous pouvons voir que les clients qui se sont détournés sont concentrés dans quelques zones de l’espace des caractéristiques de dimension inférieure.
Multi t-SNE
Pour mieux comprendre l’image, nous pouvons également la colorer avec les fonctionnalités binaires restantes : Forfait international et Messagerie vocale. Les points verts indiquent ici les objets qui sont positifs pour la caractéristique binaire correspondante.
_, axes = plt.subplots(1, 2, sharey=True, figsize=(12, 5))for i, name in enumerate(['International plan', 'Voice mail plan']):
axes[i].scatter(tsne_repr[:, 0], tsne_repr[:, 1],
c=df[name].map({'Yes': 'green', 'No': 'red'}))
axes[i].set_title(name)

Or force est de constater que, par exemple, de nombreux clients mécontents qui ont résilié leur abonnement sont entassés dans le cluster le plus au sud-ouest qui représente les personnes ayant le forfait international mais pas de messagerie vocale.
Désavantages du t-SNE
Enfin, notons quelques inconvénients dans ce tutoriel sur le t-SNE :
Grande complexité de calcul. Il est peu probable que l’implémentation dans scikit-learn soit réalisable dans une tâche réelle. Si vous avez un grand nombre d’échantillons, vous devriez plutôt essayer Multicore-TSNE.
L’intrigue peut beaucoup changer en fonction de la graine aléatoire, ce qui complique l’interprétation. Voici un bon tutoriel sur t-SNE. En général, vous ne devriez pas tirer de conclusions de grande envergure sur la base de tels graphiques, car cela peut équivaloir à de simples suppositions. Bien sûr, certaines découvertes dans les images t-SNE peuvent inspirer une idée et être confirmées par des recherches plus approfondies sur toute la ligne, mais cela n’arrive pas très souvent.
