Contenus
ToggleCART régression et classification : utilisation de l'arbre de décision
Voici un tutoriel pour l’implémentation de CART Régression et de CART Classification.
Comme cela a été expliqué, les arbres de décision sont l’approche d’apprentissage supervisé non paramétrique. En plus de la classification avec des données continues sur la cible, on retrouve aussi souvent des cas avec des données discrètes sur la cible appelés régression. Dans la régression, le moyen le plus simple peut être d’utiliser la régression linéaire pour résoudre ce cas. Cette fois, la manière de résoudre le cas de régression utilisera un arbre de décision.

CART et Moindres carrés pour la régression
Pour les arbres de régression, deux mesures d’impuretés courantes sont :
Moindres carrés. Cette méthode est similaire à la minimisation des moindres carrés dans un modèle linéaire. Les divisions sont choisies pour minimiser la somme des carrés résiduelle entre l’observation et la moyenne dans chaque nœud.
Les moindres écarts absolus. Cette méthode minimise l’écart absolu moyen par rapport à la médiane au sein d’un nœud. L’avantage de cette méthode par rapport aux moindres carrés est qu’elle n’est pas aussi sensible aux valeurs aberrantes et fournit un modèle plus robuste. L’inconvénient réside dans l’insensibilité lorsqu’il s’agit d’ensembles de données contenant une grande proportion de zéros.
CART dans les cas de classification utilise Gini Impurity dans le processus de division de l’ensemble de données en un arbre de décision. D’un autre côté, CART dans les cas de régression utilise les moindres carrés, les divisions sont choisies intuitivement pour minimiser la somme des carrés résiduelle entre l’observation et la moyenne dans chaque nœud. Afin de connaître la « meilleure » répartition, nous devons minimiser le RSS :

Découpage et optimisation
Cette simulation utilise un ensemble de données « factice » comme suit

Comme mentionné précédemment, afin de connaître la « meilleure » répartition, nous devons minimiser le RSS. tout d’abord, nous calculons RSS en le divisant en deux régions, en commençant par l’index 0
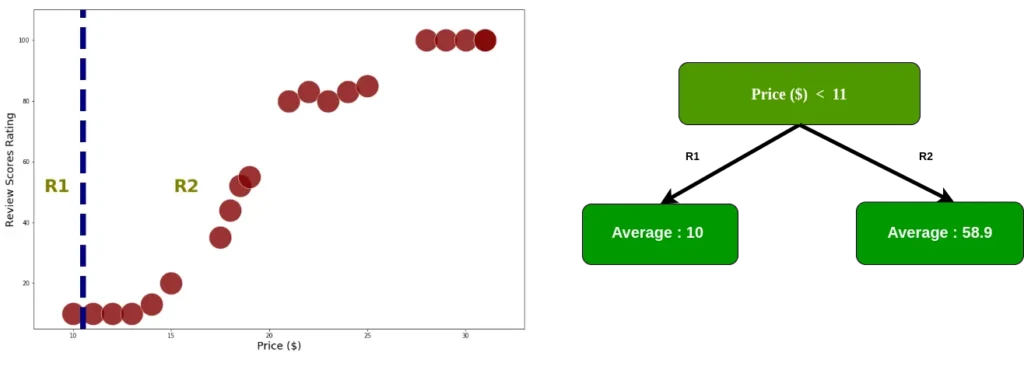
Les données étant déjà divisées en deux régions, nous additionnons le carré résiduel pour chaque donnée d’index. de plus, nous calculons RSS chaque nœud en utilisant l’équation 2.0
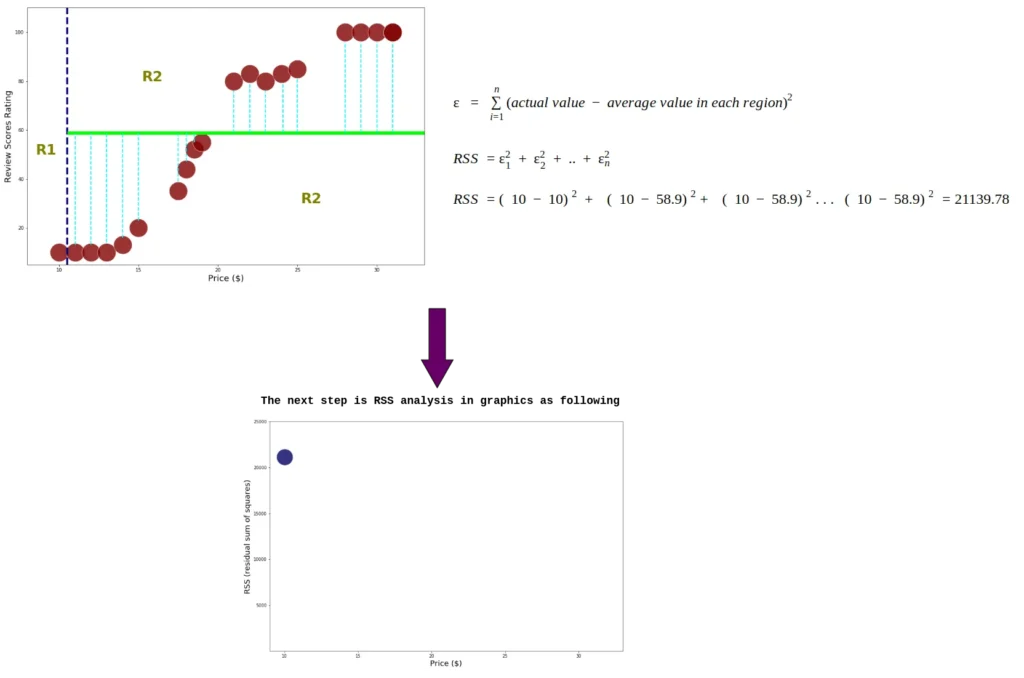
Ce processus se poursuit jusqu’au calcul du RSS dans le dernier index :

Le prix avec le seuil 19 a un RSS le plus petit, dans R1 il y a 10 données dans un prix < 19, nous allons donc diviser les données dans R1. Afin d’éviter le surajustement, nous définissons les données minimales pour chaque région >= 6. Si la région contient moins de 6 données, le processus de division dans cette région s’arrête.
Divisez les données avec le seuil 19

calculer RSS dans R1, le processus dans cette section est le même que le processus précédent, effectué uniquement pour R1. Il est possible de faire autant d’embranchement que l’on souhaite, attention a garder une masse de points consistant !

Ce qui donne l’arbre de régression suivant après 2 embranchement :

Avec de multiples colonnes
Il suffit de calculer le RSS pour chaque predicateur et de mettre en racine/embranchement celui avec le plus petit RSS (attention à utiliser un préprocessing et une métrique adéquate en cas de données non-balancées !)
CART pour la classification
Pour la classification, nous utilisons l’impureté de Gini. Nous prenons pour exemple un ensemble de données sur les maladies cardiaques comportant 303 lignes et 13 attributs. La cible comprend 138 valeurs 0 et 165 valeurs 1
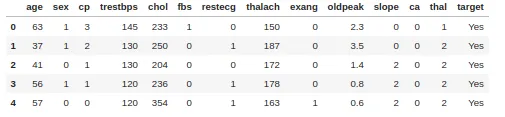
Calculons l’impureté de Gini pour la colonne Sex


Pour Fbs nous avons 0.360. Pour Exang 0.381. Fbs a la plus petite impureté de Gini, ce sera donc notre racine.
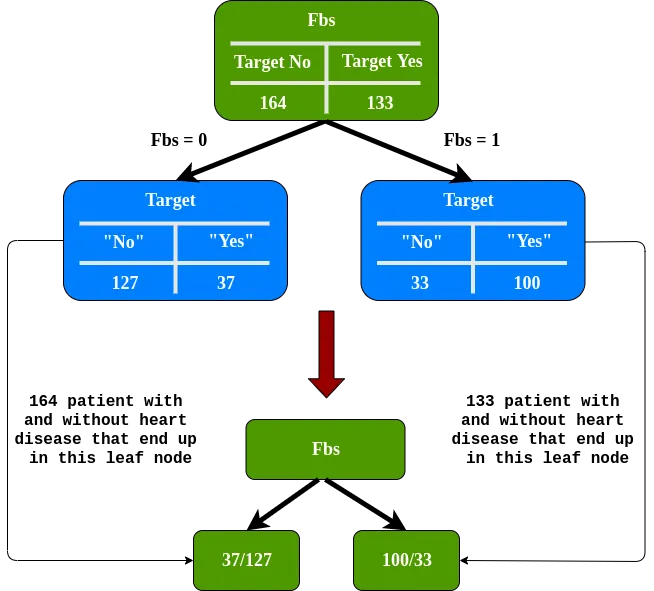
nous devons déterminer dans quelle mesure Sex et Exang séparent ces patients dans le nœud gauche de Fbs
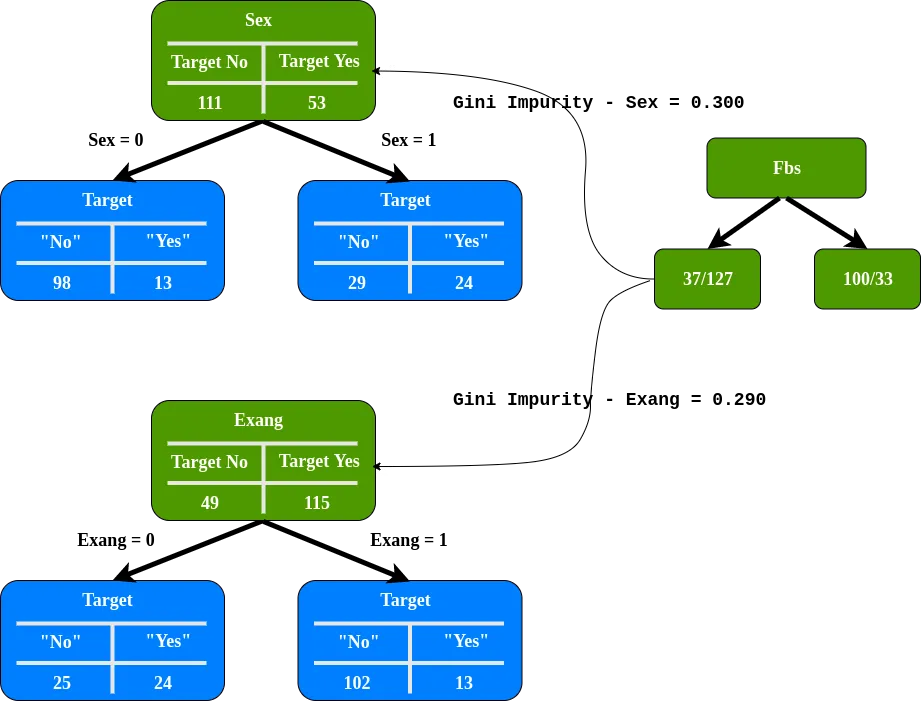
L’Exang (angor induit par l’exercice) a l’impureté Gini la plus faible, nous l’utiliserons au niveau de ce nœud pour séparer les patients.
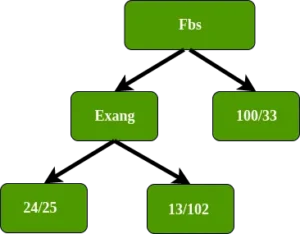
Dans le nœud gauche d’Exang, dans quelle mesure cela sépare ces 49 patients (24 avec une maladie cardiaque et 25 sans maladie cardiaque. Comme il ne reste que l’attribut sexe, nous mettons l’attribut sexe dans le nœud gauche d’Exang.
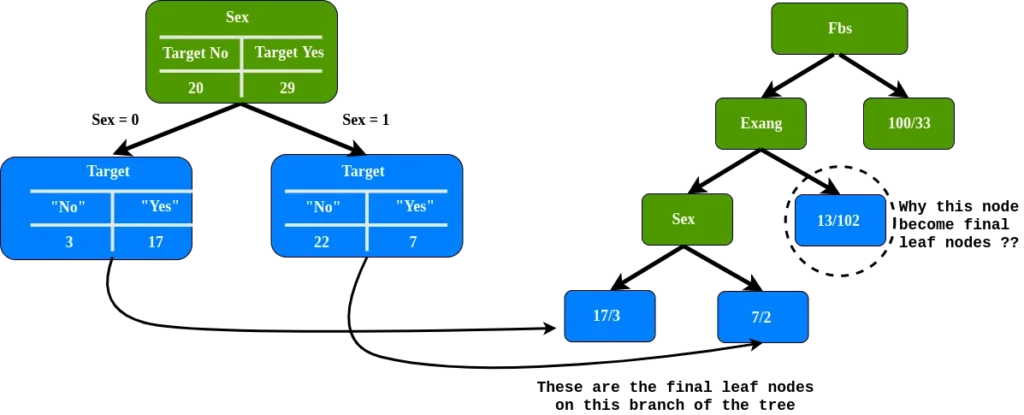
Comme nous pouvons le voir, nous avons des nœuds feuilles finaux sur cette branche, mais pourquoi le nœud feuille est-il encerclé, y compris le nœud final ?
A noter : le nœud de la feuille cerclé, 89% n’ont pas de maladies cardiaques
Ces nouvelles feuilles séparent-elles mieux les patients qu’avant ?
Afin de répondre à ces questions, nous devons comparer l’impureté de Gini en utilisant l’attribut sexe et l’impureté de Gini avant d’utiliser l’attribut sexe pour séparer les patients.

L’impureté de Gini avant d’utiliser le sexe pour séparer les patients est la plus faible, nous ne séparons donc pas ce nœud en utilisant le sexe. Le nœud final de la feuille sur cette branche de l’arbre. On fait pareil pour la branche droite de la racine, ce qui donne l’arbre de décision suivant :
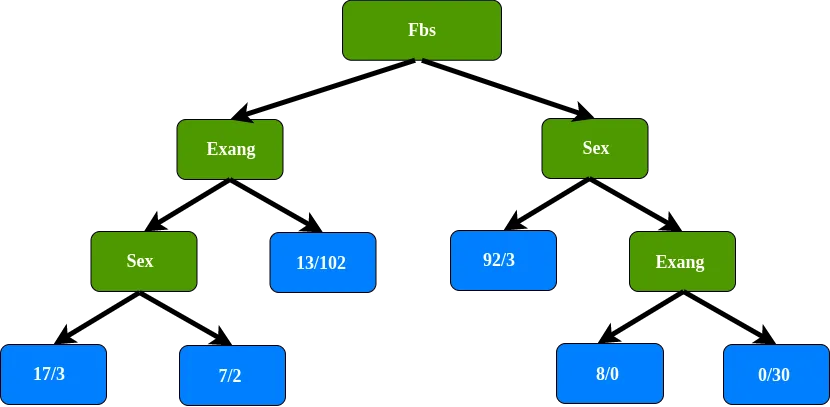
Récap' classification
Point principal lors du processus de fractionnement de l’ensemble de données
1. calculer tout le score d’impureté Gini
2. comparez le score d’impureté Gini, après n avant d’utiliser un nouvel attribut pour séparer les données. Si le nœud lui-même a le score le plus bas, il ne sert à rien de séparer les données
3. Si la séparation des données entraîne une amélioration, choisissez la séparation avec le score d’impureté le plus bas.
