Contenus
ToggleRétropropagation
Les réseaux de neurones à action directe sont inspirés par le traitement de l’information d’une ou plusieurs cellules neuronales (appelées neurones). Un neurone accepte les signaux d’entrée via son axone, qui transmettent le signal électrique au corps cellulaire. Les dendrites transmettent le signal aux synapses, qui sont les connexions des dendrites d’une cellule aux axones d’autres cellules.
Dans une synapse, l’activité électrique est convertie en activité moléculaire (molécules de neurotransmetteurs traversant la fente synaptique et se liant aux récepteurs). La liaison moléculaire développe un signal électrique qui est transmis à l’axone des cellules connectées. L’algorithme de rétropropagation est un régime d’entraînement pour les réseaux de neurones multicouches à action directe et n’est pas directement inspiré par les processus d’apprentissage du système biologique.
L’objectif de traitement de l’information de la technique est de modéliser une fonction donnée en modifiant les pondérations internes des signaux d’entrée pour produire un signal de sortie attendu. Le système est formé à l’aide d’une méthode d’apprentissage supervisé, où l’erreur entre la sortie du système et une sortie attendue connue est présentée au système et utilisée pour modifier son état interne. L’état est maintenu dans un ensemble de pondérations sur les signaux d’entrée.
Les poids sont utilisés pour représenter une abstraction de la mise en correspondance des vecteurs d’entrée avec le signal de sortie pour les exemples auxquels le système a été exposé pendant la formation. Chaque couche du réseau fournit une abstraction du traitement de l’information de la couche précédente, permettant la combinaison de sous-fonctions et d’une modélisation d’ordre supérieur.
L’algorithme de rétropropagation est une méthode d’apprentissage des poids dans un réseau neuronal à rétroaction multicouche. En tant que tel, il nécessite la définition d’une structure de réseau d’une ou plusieurs couches où une couche est entièrement connectée à la couche suivante. Une structure de réseau standard est une couche d’entrée, une couche cachée et une couche de sortie. Le procédé concerne principalement l’adaptation des poids à l’erreur calculée en présence de motifs d’entrée, et le procédé est appliqué en arrière de la couche de sortie du réseau à la couche d’entrée.
L’algorithme suivant fournit un pseudocode pour préparer un réseau à l’aide de la méthode de rétropropagation. Un poids est initialisé pour chaque entrée plus un poids supplémentaire pour une entrée biais constante qui est presque toujours fixée à 1,0. L’activation d’un seul neurone sur un modèle d’entrée donné est calculée comme suit:

où n est le nombre de poids et d’entrées, x_ki est l’attribut k-ème sur le i-ème motif d’entrée, et w_bias est le poids de biais. Une fonction de transfert logistique (sigmoïde) est utilisée pour calculer la sortie d’un neurone dans [0; 1] et fournit des non-linéarités entre les signaux d’entrée et de sortie: 1/(1+exp(-a)), où a représente l’activation des neurones.

Les mises à jour de pondération utilisent la règle delta, en particulier une règle delta modifiée dans laquelle l’erreur est propagée vers l’arrière à travers le réseau, en commençant à la couche de sortie et pondérée à travers les couches précédentes. Ce qui suit décrit la propagation inverse des mises à jour d’erreur et de poids pour un modèle unique.
Un signal d’erreur est calculé pour chaque nœud et renvoyé à travers le réseau. Pour les nœuds de sortie, il s’agit de la somme de l’erreur entre les sorties de nœud et les sorties attendues:
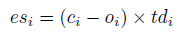
où es_i est le signal d’erreur pour le i-ème nœud, c_i est la sortie attendue et o_i est la sortie réelle pour le i-ème nœud. Le terme td est la dérivée de la sortie du i-ème nœud. Si la fonction de transfert sigmod est utilisée, td_i serait o_i*(1-o_i). Pour les nœuds cachés, le signal d’erreur est la somme des signaux d’erreur pondérés de la couche suivante.
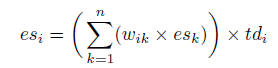
où es_i est le signal d’erreur pour le i-ème nœud, w_ik est le poids entre le i-ème et le k-ème nœuds, et es_k est le signal d’erreur du k-ème nœud.
Les dérivées d’erreur pour chaque poids sont calculées en combinant l’entrée de chaque nœud et le signal d’erreur pour le nœud.
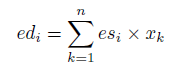
où ed_i est la dérivée d’erreur pour le i-ème nœud, es_i est le signal d’erreur pour le i-ème nœud et x_k est l’entrée du k-ème nœud dans la couche précédente. Ce processus inclut l’e biais qui a une valeur constante.
Les poids sont mis à jour dans une direction qui réduit la dérivée d’erreur ed_i (erreur affectée au poids), mesurée par un coefficient d’apprentissage.

où w_i (t + 1) est le i-ème poids mis à jour, ed_k est la dérivée d’erreur pour le k-ème nœud et learn_rate est un paramètre de coefficient de mise à jour.
L’algorithme de rétropropagation peut être utilisé pour entraîner un réseau multicouche à approximer des fonctions non linéaires arbitraires et peut être utilisé pour des problèmes de régression ou de classification.
Les valeurs d’entrée et de sortie doivent être normalisées de telle sorte que x soit dans [0;1]. Les poids initiaux sont généralement de petites valeurs aléatoires dans [0;0,5]. Les poids peuvent être mis à jour de manière en ligne (après l’exposition à chaque modèle d’entrée) ou par lots (après qu’un nombre fixe de modèles a été observé). Les mises à jour par lots devraient être plus stables que les mises à jour en ligne pour certains problèmes complexes.
Une fonction de transfert logistique (sigmoïde) est couramment utilisée pour transférer l’activation à une valeur de sortie binaire, bien que d’autres fonctions de transfert puissent être utilisées telles que la tangente hyperbolique (tanh), la gaussienne et le softmax. Il est recommandé d’exposer le système à des modèles d’entrée dans un ordre aléatoire différent à chaque itération.
Généralement, un petit nombre de couches est utilisé, de 2 à 4, étant donné que l’augmentation des couches entraîne une augmentation de la complexité du système et du temps requis pour entraîner les poids. Le taux d’apprentissage peut varier pendant la formation, et il est courant d’introduire un terme d’élan pour limiter le taux de changement. Les poids d’un réseau donné peuvent être initialisés avec une méthode d’optimisation globale avant d’être affinés à l’aide de l’algorithme de rétropropagation.
Un nœud de sortie est courant pour les problèmes de régression, tout comme un nœud de sortie par classe est courant pour les problèmes de classification.
