Contenus
ToggleRecherche tabou
La recherche tabou a été proposée par Fred Glover en 1986 (dont vous trouverez les schémas dans le déroulement de l’algorithme). La méthode utilise une mémoire (ou plusieurs mémoires) qui est mise à jour et exploitée au cours de la recherche.
À chaque itération, l’algorithme tabou choisit le meilleur voisin non tabou, même si celui-ci dégrade la fonction de coût. Pour cette raison, on dit de la recherche avec tabou qu’elle est une méthode agressive.
Liste tabou
Pour certains types de problème, l’interdiction d’un attribut peut éliminer des configurations utiles pour échapper à un optimum local. Un mécanisme, appelé critère d’aspiration, permet d’assouplir l’interdiction dans certaines conditions. Il est important de noter qu’un mauvais critère d’aspiration pour faire boucler l’algorithme sur un cycle de solutions.
Que ce soit le choix d’interdiction ou le critère d’aspiration, ces deux mécanismes doivent être adaptés au cas par cas par rapport aux problèmes rencontrés.
Déroulement de l’algorithme
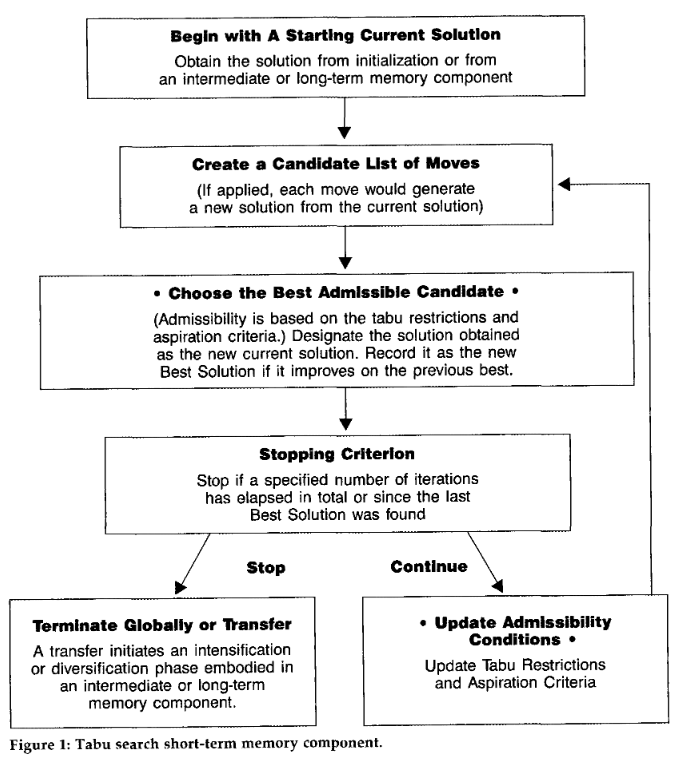
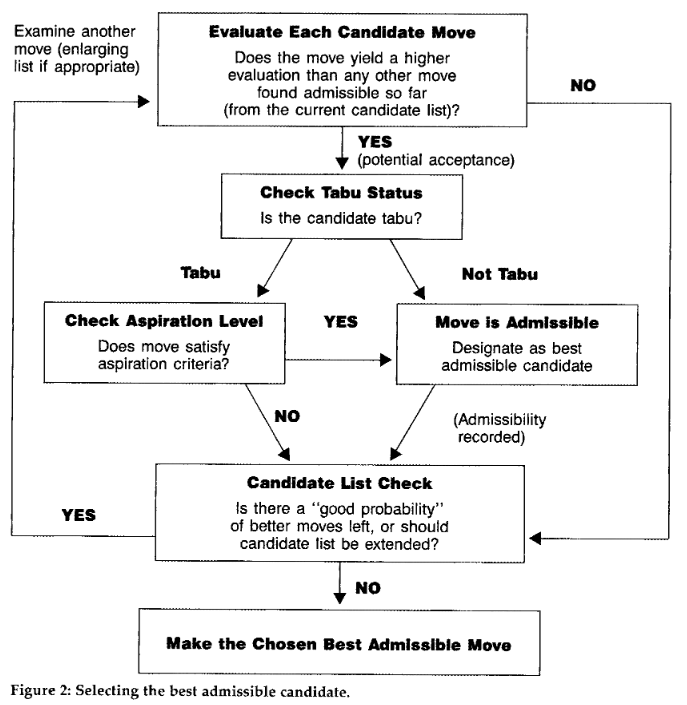
s ← s0 sBest ← s tabuList ← [] while (not stoppingCondition()) candidateList ← [] bestCandidate ← null for (sCandidate in sNeighborhood) if ( (not tabuList.contains(sCandidate)) and (fitness(sCandidate) > fitness(bestCandidate)) ) bestCandidate ← sCandidate end if end for s ← bestCandidate if (fitness(bestCandidate) > fitness(sBest)) sBest ← bestCandidate end if tabuList.push(bestCandidate); if (tabuList.size > maxTabuSize) tabuList.removeFirst() end if end while return sBes
Exemple d’application
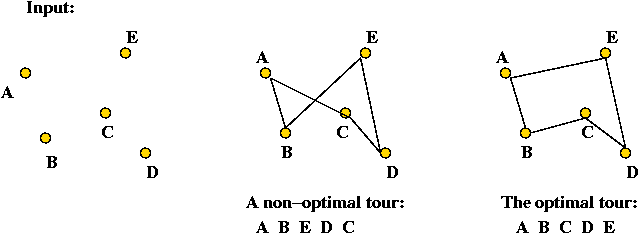
Nous prendrons l’exemple du voyageur du commerce (TSP). Soit un ensemble de villes, nous connaissons la distance entre toutes paires de villes. L’objectif est de visiter chaque ville, l’une après l’autre jusqu’à retour à la ville première, tout en minimisant la distance totale parcourue.
Le parcours est représenté par un ensemble d’arcs, les sommets étant les villes. Une configuration initiale consiste à choisir un cycle hamiltonien (un cycle qui passe une et une seule fois par chaque sommet) arbitraire, comme par exemple prendre la prochaine ville dans la liste.
Le voisinage est construit par mouvement. Un mouvement consiste à retirer deux arcs pour les « croiser ». Par exemple la paire d’arcs <(a,c), (e,b)> devient <(a,e), (c,b)>. Ainsi le cycle hamiltonien est préservé. Nous avons alors des arcs « enlevés » et des arcs « ajoutés ».
Afin de ne pas répéter le même mouvement, nous introduisons deux listes taboues : IN contenant les arcs supprimés (a,c) et (e,b); OUT contenant les arcs rajoutés (a,e) et (c,b). À chaque itération les mouvements interdits sont : introduire un arc de IN et retirer un arc de OUT. Ici l’interdiction est infinie.