Contenus
ToggleMéthode multiplicative de Holt-Winters
Voici comment fonctionne la méthode multiplicative de Holt-Winters ou triple smoothing.

Lissage exponentiel simple / Exponential Smoothing
Dans le lissage exponentiel simple (alias simple), la valeur prévue au temps i+1 est basée sur la valeur au temps i et la valeur prévue au temps i (et donc indirectement sur toutes les valeurs temporelles précédentes). En particulier, pour certains α où 0 ≤ α ≤ 1, pour tout i > 1, on définit
![]()
Notez que nous n’incluons pas le temps i = 1 dans les calculs de MAE et MSE.
En algèbre simple, cette itération peut aussi être exprimée comme
![]()
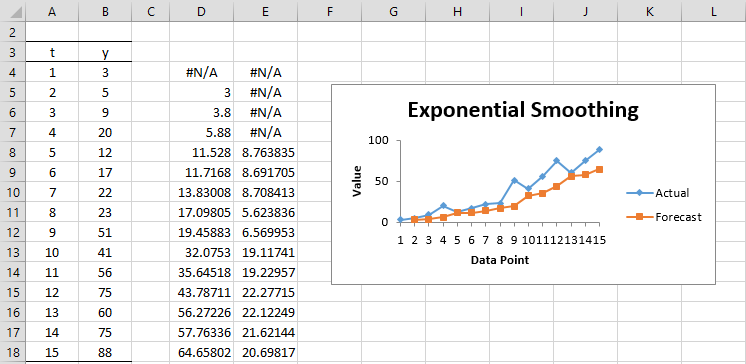
Regardons la formule avec Excel. La formule dans la cellule C4 est =B4 et la formule dans la cellule C5 est =C4+B$21*(B4-C4).

La prévision pour la prochaine valeur de la série chronologique est 74,0 (cellule C19), en utilisant la formule =C18+B$21*(B18-C18)
Excel fournit l’outil d’analyse de données Exponential Smoothing pour simplifier les calculs décrits ci-dessus.
Pour utiliser cet outil par exemple, sélectionnez Données > Analyse|Analyse des données et choisissez Lissage exponentiel dans le menu qui apparaît. Une boîte de dialogue apparaît maintenant. Un champ Facteur d’amortissement est utilisé à la place du champ Intervalle. Si ce champ est laissé vide, sa valeur par défaut est 0,7.
Le facteur d’amortissement est seulement de 1 – α. Ainsi, par exemple, vous devez utiliser 0,6 comme facteur d’amortissement.
Le résultat est présenté dans les colonnes D et E de la figure avec le graphique.
Tendance linéaire de Holt
Les données de la figure précédente du lissage exponentiel simple (ainsi que les chiffres précédents sur cette page Web) montrent une nette tendance à la hausse. Les méthodes de moyenne mobile et de lissage exponentiel simple ne modélisent pas cela de manière adéquate, mais la méthode de tendance linéaire de Holt (alias double lissage exponentiel) le fait. Ceci est accompli en ajoutant un deuxième modèle de lissage exponentiel unique pour capturer la tendance (à la hausse ou à la baisse). Le modèle prend la forme suivante pour tout i > 1.
![]()
![]()
![]()
où 0 ≤ α ≤ 1 et 0 < β ≤ 1.
Une forme alternative de ces équations est
![]()
![]()
![]()
Où![]()
Si beta=0 alors on a l’exponentiation simple.
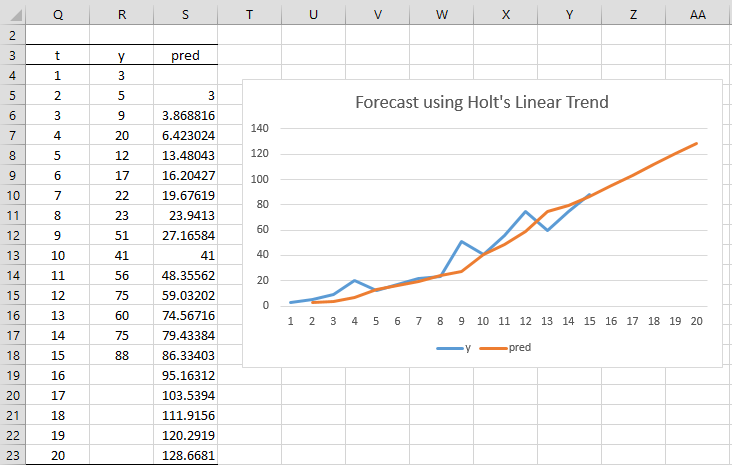
Le résultat est présenté sur la figure. Ici, la cellule C4 contient la formule =B4, la cellule D4 contient la valeur 0, la cellule C5 contient la formule =B$21*B5+(1-B$21)*(C4+D4), la cellule D5 contient la formule =C$21*( C5-C4)+(1-C$21)*D4 et la cellule E5 contient la formule =C4+D4.

Pour toute valeur de i, la prévision au temps i+h est donnée par la formule
![]()
Méthode de Holt-Winters multiplicative
Dans la méthode Holt-Winters (alias triple lissage exponentiel), nous ajoutons une composante saisonnière au modèle de tendance linéaire de Holt. Nous explorons deux de ces modèles : le modèle de saisonnalité multiplicatif et le modèle de saisonnalité additive. Nous considérons le premier de ces modèles sur cette page Web. Voir Modèle additif Holt-Winters pour le deuxième modèle.
Soit c la durée d’un cycle saisonnier. Ainsi, c = 12 pour les mois d’une année, c = 7 pour les jours d’une semaine et c = 4 pour les trimestres d’une année. Le modèle prend la forme récursive suivante pour tout i > c
![]()
![]()
![]()
où 0 ≤ α ≤ 1, 0 ≤ β ≤ 1 et 0 ≤ γ ≤ 1.
Les valeurs ui représentent la ligne de base, les valeurs vi représentent la tendance (c’est-à-dire la pente) et les valeurs si représentent la composante saisonnière. Dans le modèle multiplicatif, pour toute c périodes de temps consécutives, la somme des valeurs si est approximativement égale à c (au moins pour des valeurs raisonnables de α, β, γ).
Les prédictions pour les éléments de données yi peuvent être exprimées par
![]()
Pour les prévisions à des heures futures, nous utilisons le formulaire
![]()
où h′ =INT((h–1)/c)+1.
Formes alternatives
Nous pouvons également utiliser la version alternative suivante du terme de saisonnalité :
![]()
Sur la base de cette version du terme de saisonnalité, nous avons la forme alternative suivante des équations récursives :
![]()
![]()
![]()
Les valeurs initiales du modèle, c’est-à-dire où 1 ≤ i ≤ c, sont
![]()
Alternativement, nous pouvons fixer la valeur de tendance initiale en utilisant la pente moyenne des deux premières années, à savoir :
![]()
Notez que si γ = 0, alors le modèle Holt-Winters est équivalent au modèle de tendance linéaire de Holt, et si β = 0 et γ = 0, alors le modèle Holt-Winters est équivalent au modèle de lissage exponentiel simple.
Calculez les valeurs prévues de la série chronologique indiquée dans la plage C4:C19 de la figure à l’aide de la méthode Holt-Winter avec α = 0,5, β = 0,5 et γ = 0,5.
Le résultat est présenté sur la figure. Tout d’abord, nous calculons s1, s2, s3, s4, où c = 4, comme indiqué dans la plage F4:F7. Nous faisons cela en insérant la formule =C4/AVERAGE(C$4:C$7) dans la cellule F4, en mettant en surbrillance la plage F4:F7 et en appuyant sur Ctrl-D.
Ensuite, nous calculons uc et vc en plaçant la formule =C7/F7 dans la cellule D7 et la valeur 0 dans la cellule E7.
Nous insérons maintenant la formule =C$22*C8/F4+(1-C$22)*(D7+E7) dans la cellule D8, la formule =D$22*(D8-D7)+(1-D$22)*E7 dans la cellule E8, =E$22*(C8/D8)+(1-E$22)*F4 dans la cellule F8 et la formule =(D7+E7)*F4 dans la cellule G8, puis mettez en surbrillance la plage D8:F19 et appuyez sur Ctrl- D.
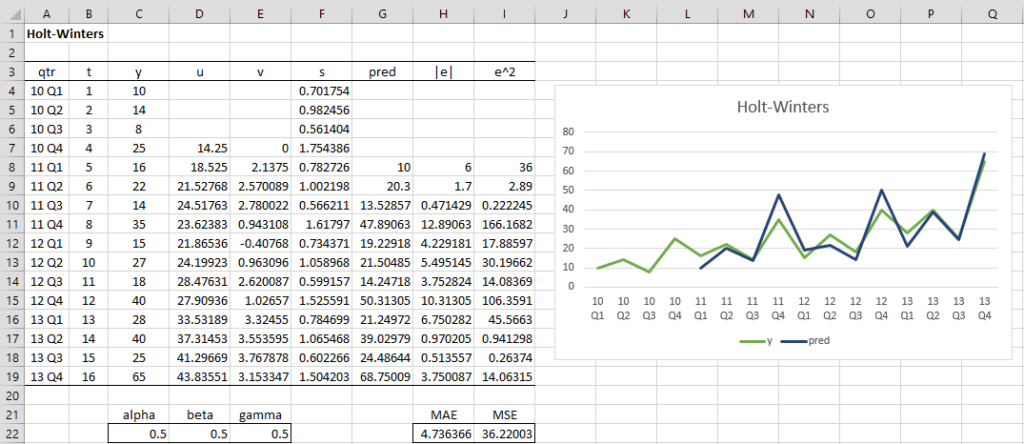
Nous pouvons utiliser Solver pour déterminer quelles valeurs d’alpha, bêta et gamma donnent le meilleur ajustement Holt-Winters pour les données de l’exemple.
L’approche d’optimisation utilisant le Solveur d’Excel est cependant susceptible de trouver un minimum local au lieu d’un minimum global. Pour cette raison, les valeurs optimisées pour alpha, bêta et gamma sont sensibles aux valeurs initiales utilisées. Vous pouvez demander à Solver d’essayer différentes valeurs initiales pour trouver les valeurs de paramètres qui réduisent la valeur de MAE.
Pour ce faire, sélectionnez Données > Analyse | Solveur et appuyez sur le bouton Options de la boîte de dialogue Solveur. La boîte de dialogue Solveur contient automatiquement les valeurs collectées par l’outil d’analyse des données Basic Forecasting. Maintenant, choisissez l’option Multistart dans l’onglet GRG Nonlinear de la boîte de dialogue Options. Le solveur s’exécutera désormais plusieurs fois en utilisant différentes valeurs de départ, en sélectionnant les valeurs qui produisent le meilleur résultat. Le coût de cette option réside dans des temps d’exécution plus lents.
Méthode additive Holt-Winters
Le modèle additif de Holt-Winters est identique au modèle multiplicatif, sauf que la saisonnalité est considérée comme additive. Cela signifie que la valeur prévue pour chaque élément de données est la somme des composants de référence, de tendance et de saisonnalité. La somme des composantes de saisonnalité pour c périodes consécutives est d’environ 1.
L’approche récursive du modèle additif est
![]()
![]()
![]()
où 0 ≤ α ≤ 1, 0 ≤ β ≤ 1 et 0 ≤ γ ≤ 1.
Les prédictions pour les éléments de données yi sont données par
![]()
Pour les prévisions à des heures futures, nous utilisons le formulaire
![]()
où h′ =INT((h–1)/c)+1.Une version alternative du terme de saisonnalité est :
![]()
Sur la base de cette version du terme de saisonnalité, nous avons la forme alternative suivante des équations récursives :
Prévoyez les valeurs y pour 2014 (c’est-à-dire les quatre prochains trimestres) à l’aide de la méthode additive de Holt-Winter basée sur les données de la plage E4:F19 de la figure en utilisant les valeurs alpha, bêta et gamma qui minimisent la statistique MSE.
C’est le même problème que l’exemple de la méthode multiplicative de Holt-Winters, sauf que nous devons maintenant appliquer la méthode additive.
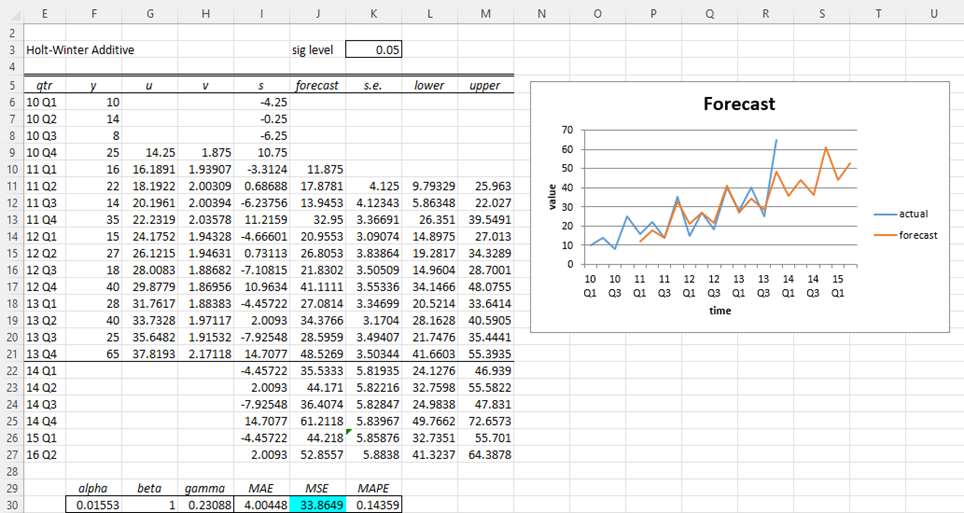
Nous pouvons calculer l’erreur standard et les intervalles de prédiction pour les prévisions du modèle additif Holt-Winters comme décrit dans Intervalle de confiance de lissage exponentiel, sauf que maintenant l’erreur standard de k pas d’avance est
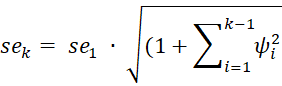
où
![]()
Les erreurs types et les intervalles de prédiction de la figure sont calculés exactement comme pour la tendance linéaire de Holt (voir Intervalle de confiance de la tendance linéaire de Holt) à l’exception de la cellule J26 puisqu’il s’agit d’une entrée où c|i-1. La formule dans la cellule J26 est
=22 K$*SQRT((K25/K$22)^2-1+(F$30*(1+(ROW(J26)-ROW(J$22))*G$30+(1-F$30)*H$30) )^2+1)
Le terme (1-F$30)*H$30 dans cette formule ne se trouve pas dans les autres formules d’erreur type (bien qu’un tel terme soit inclus dans les 5 pas d’avance, 9 pas d’avance, 13 pas d’avance, etc. erreurs types).
