Contenido
PalancaMétodo multiplicativo de Holt-Winters
Así funciona el método de suavizado multiplicativo o triple de Holt-Winters.

Suavizado exponencial simple
En el suavizado exponencial simple (también conocido como simple), el valor predicho en el momento i+1 se basa en el valor en el momento i y el valor predicho en el momento i (y, por lo tanto, indirectamente en todos los valores de tiempo anteriores). En particular, para algún α donde 0 ≤ α ≤ 1, para todo i > 1, definimos
![]()
Tenga en cuenta que no incluimos el tiempo i = 1 en los cálculos de MAE y MSE.
En álgebra simple, esta iteración también se puede expresar como
![]()
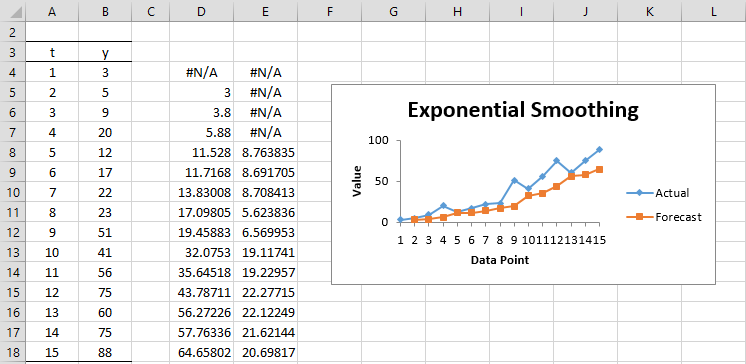
Veamos la fórmula con Excel. La fórmula en la celda C4 es =B4 y la fórmula en la celda C5 es =C4+B$21*(B4-C4).

El pronóstico para el siguiente valor en la serie temporal es 74,0 (celda C19), usando la fórmula =C18+B$21*(B18-C18)
Excel proporciona la herramienta de análisis de datos de suavizado exponencial para simplificar los cálculos descritos anteriormente.
Para utilizar esta herramienta, por ejemplo, seleccione Datos > Análisis|Análisis de datos y elija Suavizado exponencial en el menú que aparece. Ahora aparece un cuadro de diálogo. Se utiliza un campo Factor de amortiguación en lugar del campo Intervalo. Si este campo se deja en blanco, su valor predeterminado es 0,7.
El factor de amortiguación es sólo 1 – α. Así, por ejemplo, debería utilizar 0,6 como factor de amortiguación.
El resultado se presenta en las columnas D y E de la figura con el gráfico.
tendencia lineal de Holt
Los datos de la figura anterior de suavizado exponencial simple (así como las cifras anteriores de esta página web) muestran una clara tendencia al alza. Los métodos de media móvil y de suavizado exponencial único no modelan esto adecuadamente, pero el método de tendencia lineal de Holt (también conocido como suavizado doble exponencial) sí lo hace. Esto se logra agregando un segundo modelo de suavizado exponencial único para capturar la tendencia (al alza o a la baja). El modelo toma la siguiente forma para todo i > 1.
![]()
![]()
![]()
donde 0 ≤ α ≤ 1 y 0 < β ≤ 1.
Una forma alternativa de estas ecuaciones es
![]()
![]()
![]()
O![]()
Si beta=0 entonces tenemos una exponenciación simple.
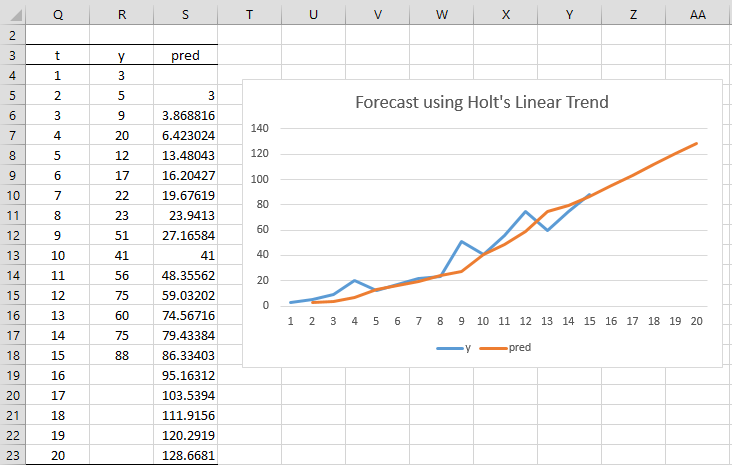
El resultado se presenta en la figura. Aquí, la celda C4 contiene la fórmula =B4, la celda D4 contiene el valor 0, la celda C5 contiene la fórmula =B$21*B5+(1-B$21)*(C4+D4), la celda D5 contiene la fórmula =C$21* (C5-C4 )+(1-C$21)*D4 y la celda E5 contiene la fórmula =C4+D4.

Para cualquier valor de i, el pronóstico en el momento i+h viene dado por la fórmula
![]()
Método multiplicativo de Holt-Winters
En el método Holt-Winters (también conocido como suavizado triple exponencial), agregamos un componente estacional al modelo de tendencia lineal de Holt. Exploramos dos de estos modelos: el modelo de estacionalidad multiplicativa y el modelo de estacionalidad aditiva. Consideramos el primero de estos modelos en esta página web. Consulte el modelo aditivo de Holt-Winters para el segundo modelo.
Sea c la duración de un ciclo estacional. Así, c = 12 para los meses de un año, c = 7 para los días de una semana y c = 4 para los trimestres de un año. El modelo toma la siguiente forma recursiva para todo i > c
![]()
![]()
![]()
donde 0 ≤ α ≤ 1, 0 ≤ β ≤ 1 y 0 ≤ γ ≤ 1.
Los valores de ui representan la línea de base, los valores de vi representan la tendencia (es decir, la pendiente) y los valores de si representan el componente estacional. En el modelo multiplicativo, para cualquier c períodos de tiempo consecutivos, la suma de los valores de si es aproximadamente igual a c (al menos para valores razonables de α, β, γ).
Las predicciones para los elementos de datos yi se pueden expresar como
![]()
Para pronósticos en tiempos futuros, utilizamos el formulario
![]()
donde h′ =INT((h–1)/c)+1.
Formas alternativas
También podemos utilizar la siguiente versión alternativa del término estacionalidad:
![]()
Con base en esta versión del término de estacionalidad, tenemos la siguiente forma alternativa de las ecuaciones recursivas:
![]()
![]()
![]()
Los valores iniciales del modelo, es decir, donde 1 ≤ i ≤ c, son
![]()
Alternativamente, podemos establecer el valor de la tendencia inicial utilizando la pendiente promedio de los dos primeros años, a saber:
![]()
Tenga en cuenta que si γ = 0, entonces el modelo de Holt-Winters es equivalente al modelo de tendencia lineal de Holt, y si β = 0 y γ = 0, entonces el modelo de Holt-Winters es equivalente al modelo de suavizado exponencial simple.
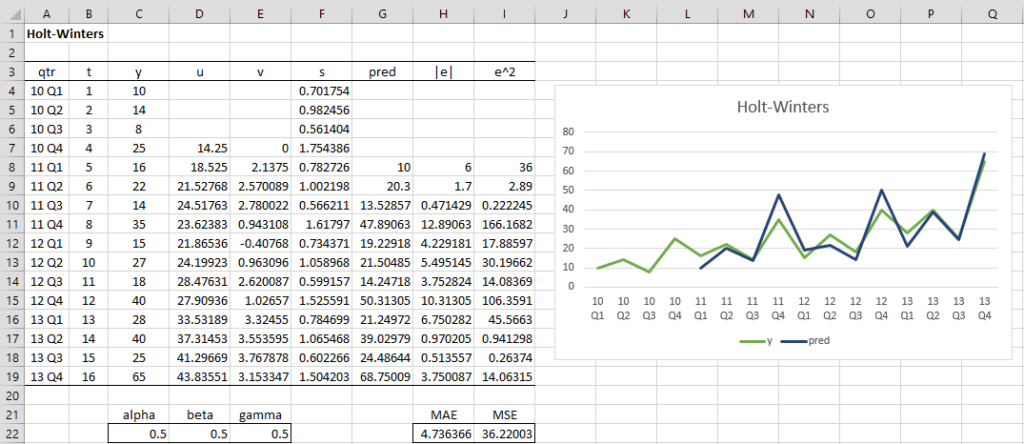
Calcule los valores predichos de la serie temporal que se muestra en el rango C4:C19 de la figura utilizando el método Holt-Winter con α = 0,5, β = 0,5 y γ = 0,5.
El resultado se presenta en la figura. Primero, calculamos s1, s2, s3, s4, donde c = 4, como se muestra en el rango F4:F7. Hacemos esto insertando la fórmula =C4/PROMEDIO(C$4:C$7) en la celda F4, resaltando el rango F4:F7 y presionando Ctrl-D.
A continuación, calculamos uc y vc colocando la fórmula =C7/F7 en la celda D7 y el valor 0 en la celda E7.
Ahora insertamos la fórmula =C$22*C8/F4+(1-C$22)*(D7+E7) en la celda D8, la fórmula =D$22*(D8-D7)+(1-D$22)*E7 en la celda E8, =E$22 *(C8/D8)+(1-E$22)*F4 en la celda F8 y la fórmula =(D7+E7)*F4 en la celda G8, luego resalte el rango D8:F19 y presione Ctrl-D.
Podemos usar Solver para determinar qué valores de alfa, beta y gama proporcione el mejor ajuste de Holt-Winters para los datos de ejemplo.
Sin embargo, es probable que el enfoque de optimización que utiliza Excel Solver encuentre un mínimo local en lugar de un mínimo global. Por esta razón, los valores optimizados para alfa, beta y gamma son sensibles a los valores iniciales utilizados. Puede pedirle a Solver que pruebe diferentes valores iniciales para encontrar los valores de los parámetros que reducen el valor MAE.
Para hacer esto, seleccione Datos > Análisis | Solver y presione el botón Opciones en el cuadro de diálogo Solver. El cuadro de diálogo Solver contiene automáticamente los valores recopilados por la herramienta de análisis de datos de Pronóstico básico. Ahora elija la opción Multistart en la pestaña GRG Nonlinear del cuadro de diálogo Opciones. El solucionador ahora se ejecutará varias veces utilizando diferentes valores iniciales, seleccionando los valores que produzcan el mejor resultado. El costo de esta opción son tiempos de ejecución más lentos.
Método aditivo de Holt-Winters
El modelo aditivo de Holt-Winters es idéntico al modelo multiplicativo, excepto que la estacionalidad se considera aditiva. Esto significa que el valor previsto para cada elemento de datos es la suma de los componentes de referencia, tendencia y estacional. La suma de los componentes de estacionalidad para c períodos consecutivos es aproximadamente 1.
El enfoque recursivo del modelo aditivo es
![]()
![]()
![]()
donde 0 ≤ α ≤ 1, 0 ≤ β ≤ 1 y 0 ≤ γ ≤ 1.
Las predicciones para los elementos de datos yi están dadas por
![]()
Para pronósticos en tiempos futuros, utilizamos el formulario
![]()
donde h′ =INT((h–1)/c)+1. Una versión alternativa del término de estacionalidad es:
![]()
Con base en esta versión del término de estacionalidad, tenemos la siguiente forma alternativa de las ecuaciones recursivas:
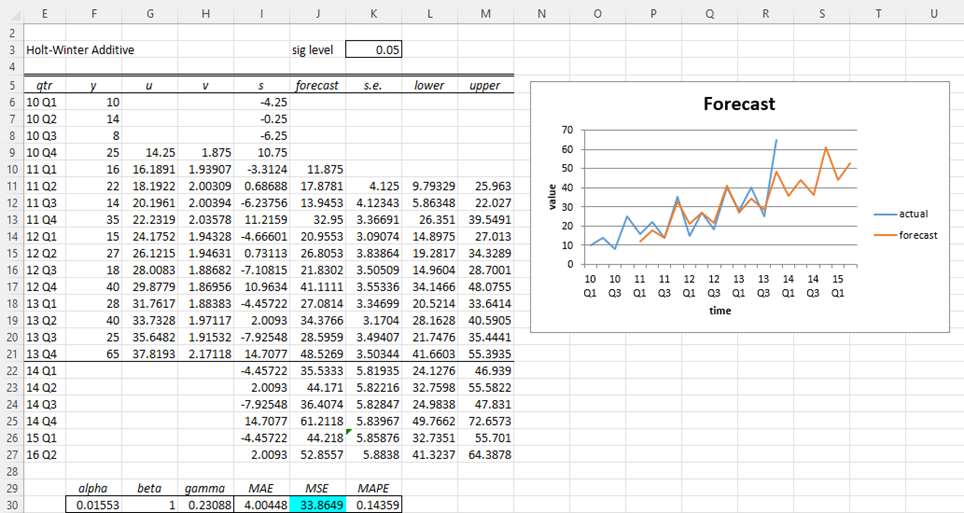
Pronostique los valores de y para 2014 (es decir, los próximos cuatro trimestres) utilizando el método aditivo de Holt-Winter basado en datos del rango E4:F19 de la figura utilizando valores alfa, beta y gamma que minimizan la estadística MSE.
Este es el mismo problema que el ejemplo del método multiplicativo de Holt-Winters, excepto que ahora necesitamos aplicar el método aditivo.
Podemos calcular el error estándar y los intervalos de predicción para los pronósticos del modelo aditivo de Holt-Winters como se describe en Intervalo de confianza de suavizado exponencial, excepto que ahora el error estándar de k pasos adelante es
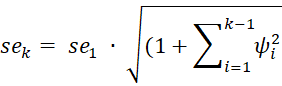
o
![]()
Los errores estándar y los intervalos de predicción en la figura se calculan exactamente igual que para la tendencia lineal de Holt (consulte el intervalo de confianza de la tendencia lineal de Holt), con la excepción de la celda J26, ya que es una entrada donde c|i-1. La fórmula en la celda J26 es
=22 K$*SQRT((K25/K$22)^2-1+(F$30*(1+(FILA(J26)-FILA(J$22))*G$30+(1-F$30)*H$30) )^2+1)
El término (1-F$30)*H$30 en esta fórmula no se encuentra en otras fórmulas de error estándar (aunque dicho término se incluye en los errores estándar de avance de 5 pasos, avance de 9 pasos, avance de 13 pasos, etc.).
