Contenido
PalancaPrueba de Diebold-Mariano y HLN
Aquí en detalle la prueba de Diebold-Mariano y la medición de Harvey, Leybourne y Newbold.

Bases
Supongamos que tenemos dos pronósticos f1,…, fn y g1,…, gn para una serie de tiempo si y1,…, yn y queremos ver cuál pronóstico es mejor, en el sentido de que tiene la mejor precisión predictiva. El enfoque obvio es seleccionar el pronóstico que tenga la medida de error más pequeña basándose en una de las medidas de error descritas en Errores de pronóstico. Pero necesitamos ir más allá y determinar si esta diferencia es significativa (con fines predictivos) o simplemente se debe a la elección específica de los valores de los datos en la muestra.
Utilizamos la prueba de Diebold-Mariano para determinar si las dos predicciones son significativamente diferentes. Sean ei y ri los residuos de los dos pronósticos, es decir
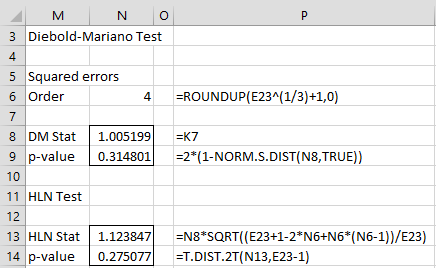
![]()
y se define como una de las siguientes medidas (u otras medidas similares):
![]()
La serie temporal di se denomina pérdida diferencial. Obviamente, la primera de estas fórmulas está relacionada con la estadística de error MSE y la segunda está relacionada con la estadística de error MAE. ahora definimos
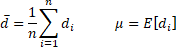
Para n > k ≥ 1, definimos
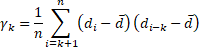
Como se describe en la función de autocorrelación, γk es la autocovarianza en el retraso k.
Para h ≥ 1, defina el estadístico de Diebold-Mariano de la siguiente manera:
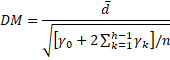
Generalmente es suficiente utilizar el valor h = n1/3 + 1.
Bajo el supuesto de que μ = 0 (la hipótesis nula), DM sigue una distribución normal estándar:
DM ∼ N(0, 1)
Por tanto, existe una diferencia significativa entre las previsiones si |DM| > zcrit donde zcrit es el valor crítico bilateral para la distribución normal estándar; es decir.
zcrit = DISTR.NORM.S.(1–α/2, VERDADERO)
El supuesto clave para utilizar la prueba de Diebold-Mariano es que la serie temporal de pérdidas diferenciales di es estacionaria (consulte Serie temporal estacionaria).
Utilice la prueba de Diebold-Mariano para determinar si existe una diferencia significativa en las predicciones de las columnas B y C de la Figura 1 para los datos de la columna A.
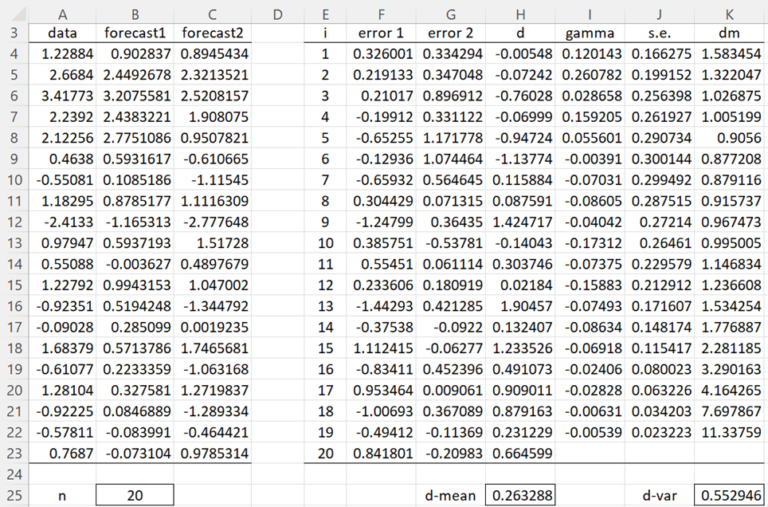
Cálculo con Excel
Comenzamos calculando los residuos de los 20 elementos de datos en función de las dos predicciones (columnas F y G). Por ejemplo. la celda F4 contiene la fórmula =A4-B4 y la celda G4 contiene =A4-C4. A partir de estos valores podemos calcular los diferenciales de pérdidas en la columna H. Ej. la celda H4 contiene =F4^2-G4^2. Ahora podemos calcular la media y la varianza de la serie temporal di mediante las fórmulas =PROMEDIO(H4:H23) y =VAR.P(H4:H23), como se muestra en las celdas H25 y K25.
Los valores de γi ahora se pueden calcular como se muestra en la columna I. Por ej. la celda I4 contiene la fórmula matricial
=SUMPRODUCTO(H5:H$23-H$25,OFFSET(H$4:H$23,0,0,E$23-E4)-H$25)/E$23
Alternativamente, la celda I4 se puede calcular usando la fórmula =ACVF(H$4:H$23,E4), como se describe en Función de autocorrelación. Luego se pueden calcular los errores estándar (columna J) y los estadísticos de Diebold-Mariano (columna K). Por ejemplo. la celda J4 contiene la fórmula =SQRT(J25/E23), la celda J5 contiene =SQRT((J$25+2*SUMPRODUCT(I$4:I4))/E$23) (y lo mismo para las otras celdas en la columna J) y la celda K4 contiene la fórmula =G$25/J4.
Podemos leer los valores estadísticos de DM de la columna K. Por ejemplo. el estadístico DM para el orden h = 4 es 1,005199, como se muestra en la celda K7. Tenga en cuenta que, dado que h = n1/3 + 1 = 201/3 + 1 = 3,7, h = 4 parece un buen valor de orden para usar. Dado que el valor p = 2*(1-NORM.S.DIST(K7,TRUE)) = 0,3148 > 0,05 = α, concluimos que no existe una diferencia significativa entre las dos predicciones.
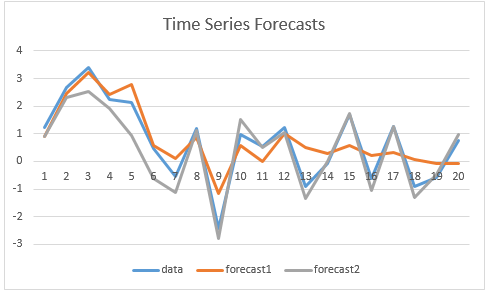
En la figura, trazamos ambas predicciones para los datos de la columna A, de modo que usted pueda juzgar por sí mismo si el gráfico es consistente con los resultados de la prueba de Diebold-Mariano.
prueba HLN
La prueba de Diebold-Mariano tiende a rechazar la hipótesis nula con demasiada frecuencia para muestras pequeñas. Una prueba mejor es la prueba de Harvey, Leybourne y Newbold (HLN), que se basa en lo siguiente:
Sobre todo porque, por ejemplo, tenemos una muestra pequeña, utilizamos la prueba HLN como se muestra en la figura. Una vez más vemos que no hay diferencia significativa entre las previsiones.