Contenus
ToggleTest de Diebold-Mariano et HLN
Voici en détail le test de Diebold-Mariano et la mesure de Harvey, Leybourne, and Newbold.

Bases
Supposons que nous ayons deux prévisions f1, …, fn et g1, …, gn pour une série chronologique si y1, …, yn et que nous voulions voir quelle prévision est la meilleure, dans le sens où elle a la meilleure précision prédictive. L’approche évidente consiste à sélectionner la prévision qui présente la mesure d’erreur la plus petite en fonction de l’une des mesures d’erreur décrites dans Erreurs de prévision. Mais nous devons aller plus loin et déterminer si cette différence est significative (à des fins prédictives) ou simplement due au choix spécifique des valeurs de données dans l’échantillon.
Nous utilisons le test de Diebold-Mariano pour déterminer si les deux prévisions sont significativement différentes. Soit ei et ri les résidus des deux prévisions, c’est-à-dire
![]()
et soit défini comme l’une des mesures suivantes (ou d’autres mesures similaires)
![]()
La série chronologique di est appelée perte différentielle. De toute évidence, la première de ces formules est liée à la statistique d’erreur MSE et la seconde est liée à la statistique d’erreur MAE. Nous définissons maintenant
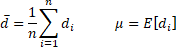
Pour n > k ≥ 1, on définit
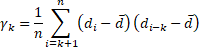
Comme décrit dans la fonction d’autocorrélation, γk est l’autcovariance au décalage k.
Pour h ≥ 1, définissez la statistique Diebold-Mariano comme suit :
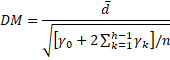
Il suffit généralement d’utiliser la valeur h = n1/3 + 1.
Sous l’hypothèse que μ = 0 (l’hypothèse nulle), DM suit une distribution normale standard :
DM ∼ N(0, 1)
Il existe donc une différence significative entre les prévisions si |DM| > zcrit où zcrit est la valeur critique bilatérale pour la distribution normale standard ; c’est à dire.
zcrit = NORM.S.DIST(1–α/2, VRAI)
L’hypothèse clé pour l’utilisation du test de Diebold-Mariano est que la série chronologique différentielle de pertes di est stationnaire (voir Série chronologique stationnaire).
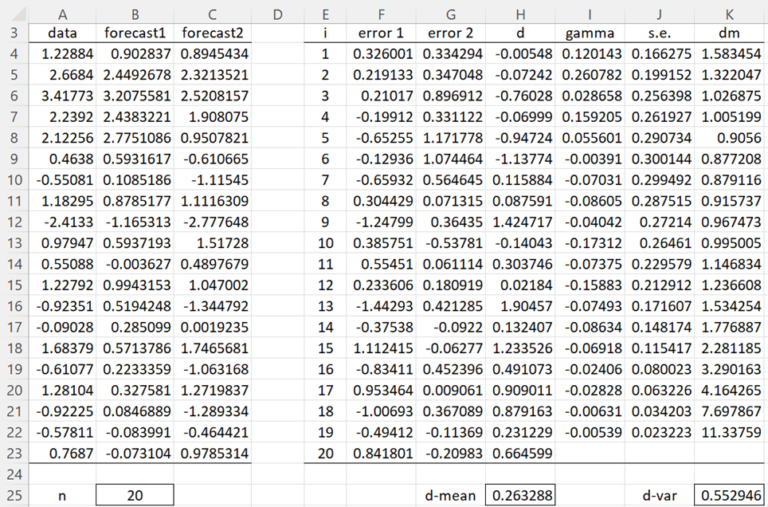
Utilisez le test de Diebold-Mariano pour déterminer s’il existe une différence significative dans les prévisions des colonnes B et C de la figure 1 pour les données de la colonne A.
Calcul avec Excel
Nous commençons par calculer les résidus pour les 20 éléments de données en fonction des deux prévisions (colonnes F et G). Par exemple. la cellule F4 contient la formule =A4-B4 et la cellule G4 contient =A4-C4. À partir de ces valeurs, nous pouvons calculer les différentiels de pertes dans la colonne H. Par ex. la cellule H4 contient =F4^2-G4^2. Nous pouvons maintenant calculer la moyenne et la variance de la série chronologique di via les formules =AVERAGE(H4:H23) et =VAR.P(H4:H23), comme indiqué dans les cellules H25 et K25.
Les valeurs γi peuvent maintenant être calculées comme indiqué dans la colonne I. Par ex. la cellule I4 contient la formule matricielle
=SOMMEPRODUIT(H5:H$23-H$25,OFFSET(H$4:H$23,0,0,E$23-E4)-H$25)/E$23
Alternativement, la cellule I4 peut être calculée à l’aide de la formule =ACVF(H$4:H$23,E4), comme décrit dans Fonction d’autocorrélation. Les erreurs types (colonne J) et les statistiques de Diebold-Mariano (colonne K) peuvent ensuite être calculées. Par exemple. la cellule J4 contient la formule =SQRT(J25/E23), la cellule J5 contient =SQRT((J$25+2*SUMPRODUCT(I$4:I4))/E$23) (et de même pour les autres cellules de la colonne J) et la cellule K4 contient la formule =G$25/J4.
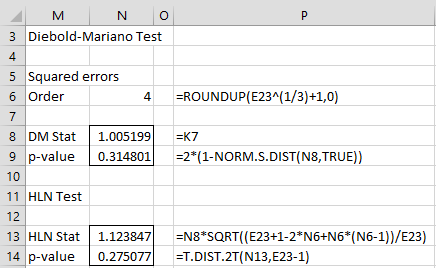
Nous pouvons lire les valeurs statistiques DM de la colonne K. Par exemple. la statistique DM pour l’ordre h = 4 est 1,005199, comme indiqué dans la cellule K7. Notez que puisque h = n1/3 + 1 = 201/3 + 1 = 3,7, h = 4 semble être une bonne valeur d’ordre à utiliser. Puisque la valeur p = 2*(1-NORM.S.DIST(K7,TRUE)) = 0,3148 > 0,05 = α, nous concluons qu’il n’y a pas de différence significative entre les deux prévisions.
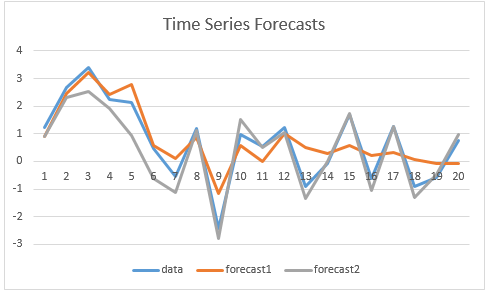
Dans la figure, nous traçons les deux prévisions pour les données de la colonne A, et vous pouvez ainsi juger par vous-même si le graphique est cohérent avec les résultats du test Diebold-Mariano.
Test de HLN
Le test de Diebold-Mariano a tendance à rejeter trop souvent l’hypothèse nulle pour les petits échantillons. Un meilleur test est le test de Harvey, Leybourne et Newbold (HLN), qui est basé sur les éléments suivants :
D’autant plus que par exemple nous avons un petit échantillon, nous utilisons le test HLN comme le montre la figure. Encore une fois, on constate qu’il n’y a pas de différence significative entre les prévisions.