Contenus
ToggleTest de Dickey-Fuller
Le test de Dickey-Fuller est un moyen de déterminer si le processus (série temporelle) a une racine unitaire.

Bases
Nous considérons le processus stochastique de forme
![]()
où |φ| ≤ 1 et εi est un bruit blanc. Si |φ| = 1, on a ce qu’on appelle une racine unitaire. En particulier, si φ = 1, on a une marche aléatoire (sans dérive), qui n’est pas stationnaire. En fait, si |φ| = 1, le processus n’est pas stationnaire, alors que si |φ| < 1, le processus est stationnaire. Nous ne considérerons pas le cas où |φ| > 1 de plus puisque dans ce cas le processus est dit explosif et s’accentue avec le temps.
Ce processus est un processus autorégressif de premier ordre, AR(1), que nous étudions plus en détail dans Processus autorégressifs. Nous verrons également pourquoi de tels processus sans racine unitaire sont stationnaires et pourquoi le terme « racine » est utilisé.
Le test de Dickey-Fuller est un moyen de déterminer si le processus ci-dessus a une racine unitaire. L’approche utilisée est assez simple. Calculez d’abord la première différence, c’est-à-dire
![]()
c’est-à-dire
Si nous utilisons l’opérateur delta, défini par Δyi = yi – yi-1 et définissons β = φ – 1, alors l’équation devient l’équation de régression linéaire
![]()
où β ≤ 0 et donc le test pour φ est transformé en un test selon lequel le paramètre de pente β = 0. Ainsi, nous avons un test unilatéral (puisque β ne peut pas être positif) où
H0 : β = 0 (équivalent à φ = 1)
H1 : β < 0 (équivalent à φ < 1)
Sous l’hypothèse alternative, si b est l’estimation des moindres carrés ordinaires (MCO) de β, et donc φ-bar = 1 + b est l’estimation des moindres carrés ordinaires (MCO) de φ, alors pour n suffisamment grand
![]()
où
Nous pouvons utiliser l’approche de régression linéaire habituelle, sauf que lorsque l’hypothèse nulle est vérifiée, le coefficient t ne suit pas une distribution normale et nous ne pouvons donc pas utiliser le test t habituel. Au lieu de cela, ce coefficient suit une distribution tau, et notre test consiste donc à déterminer si la statistique tau τ (qui est équivalente à la statistique t habituelle) est inférieure à τcrit sur la base d’un tableau de valeurs statistiques tau critiques présenté dans le tableau Dickey-Fuller. .
Si la valeur tau calculée est inférieure à la valeur critique du tableau des valeurs critiques, alors nous avons un résultat significatif ; sinon, nous acceptons l’hypothèse nulle selon laquelle il existe une racine unitaire et que la série chronologique n’est pas stationnaire.
Il existe les trois versions suivantes du test de Dickey-Fuller :
Type 0 Pas de constante, pas de tendance Δyi = β1 yi-1 + εi
Type 1 Constante, pas de tendance Δyi = β0 + β1 yi-1 + εi
Type 2 Constante et tendance Δyi = β0 + β1 yi-1 + β2 i+ εi
Chaque version du test utilise un ensemble différent de valeurs critiques, comme indiqué dans le tableau Dickey-Fuller. Il est important de sélectionner la version correcte du test pour la série chronologique analysée. Notez que le test de type 2 suppose qu’il existe un terme constant (qui peut être significativement égal à zéro).
Exemple
Les gains quotidiens nets d’un petit joueur sont répertoriés dans la colonne B de la figure 1. Utilisez le test de Dickey-Fuller pour déterminer si la série chronologique est stationnaire.
Nous commençons par supposer que le bon modèle est de type 1, à savoir constant mais sans tendance.
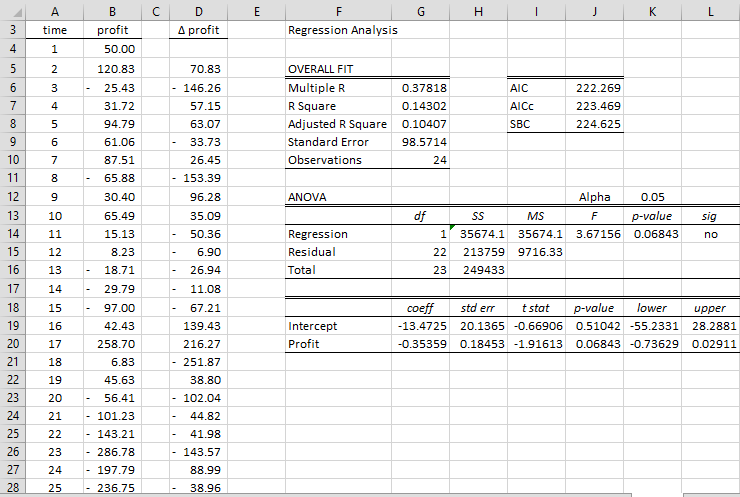
Puisque nous utilisons le modèle de régression
(constante, pas de tendance), nous utilisons l’outil d’analyse de données de régression linéaire Real Statistics en utilisant la plage B4 : B27 et la plage de données X et D5 : D28 comme plage de données Y. Notez que les valeurs de la colonne D sont calculées en plaçant la formule =B5-B4 dans la cellule D5, en mettant en surbrillance la plage D5:D28 et en appuyant sur Ctrl-D.
Le résultat de l’analyse de régression est présenté sur le côté droit de la figure. En particulier, nous voyons que la statistique t (cellule I20) pour le coefficient β1 est de -1,91613. C’est la statistique tau. Nous regardons maintenant dans le tableau Dickey-Fuller et constatons que la valeur critique de tau pour un test de type 1 est de -2,986 lorsque n = 25 et α = 0,05. Puisque τcrit = -2,986 < – 1,91613 = τ, nous ne pouvons pas rejeter l’hypothèse nulle selon laquelle la série chronologique n’est pas stationnaire.
Notez que le coefficient β1 (cellule G20) est négatif comme prévu. Si au contraire le coefficient était positif, alors nous saurions que ce type de test de Dickey-Fuller est inapproprié puisque β1 = φ – 1 ≤ 0.
Nous affichons maintenant dans la figure un tracé des valeurs des séries chronologiques de la figure précédente.
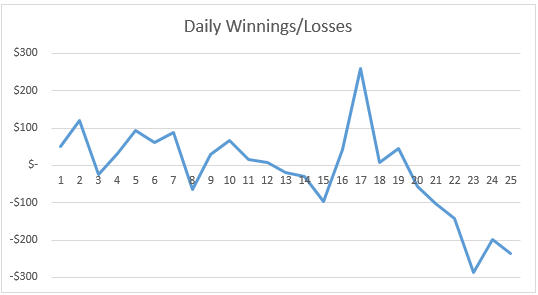
Nous constatons une tendance apparente à la baisse vers la fin de la période de 25 jours et il n’est donc pas surprenant que la série chronologique ne soit pas stationnaire. En fait, cela nous amène à choisir le test de Dickey-Fuller de type 2 (avec constante et tendance). Le résultat de ce test est présenté sur la figure.
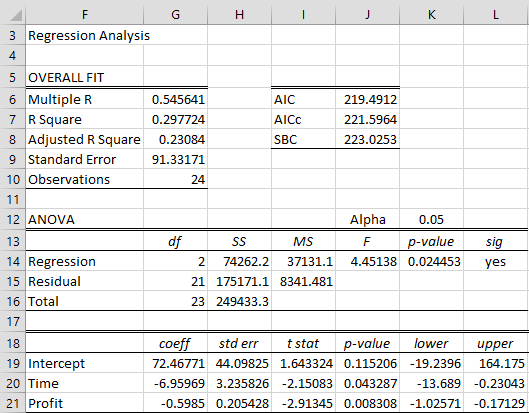
Puisque nous utilisons le modèle de régression
Δyi = β0 + β1i + β2yi-1 + εi
cette fois, nous utilisons A4:B27 de la figure 1 comme plage de données X et D5:D28 comme plage de données Y. Nous voyons sur la figure 3 que la statistique t (cellule I21) pour le coefficient β2 est de -2,91345. Nous regardons maintenant dans le tableau Dickey-Fuller et constatons que la valeur critique de tau est de -3,60269 pour un test de type 2 lorsque n = 25 et α = 0,05. Puisque τcrit = -3,60269 < -2,91345 = τ, nous ne pouvons pas rejeter l’hypothèse nulle selon laquelle la série chronologique n’est pas stationnaire.
