Contenus
ToggleDétection des anomalies dans les séries temporelles
Ce tutoriel répond à la problématique de la détection des anomalies en préprocessing pour le forecasting des séries temporelles.

Contexte
Lors de l’analyse des données de séries chronologiques, nous devons nous assurer des valeurs aberrantes, tout comme nous le faisons pour les données statiques. Si vous avez travaillé avec des données à quelque titre que ce soit, vous savez à quel point les valeurs aberrantes sont pénibles pour un analyste. Ces valeurs aberrantes sont appelées « anomalies » dans le jargon des séries chronologiques.
Le code de Aayush Bajaj, à l’origine de ce tutoriel, est disponible : PIPELINE
D’un point de vue traditionnel, une valeur aberrante/anomalie est :
« Une observation qui s’écarte tellement des autres observations qu’elle fait soupçonner qu’elle a été générée par un mécanisme différent. »
Par conséquent, vous pouvez considérer les valeurs aberrantes (outliers) comme des observations qui ne suivent pas le comportement attendu.
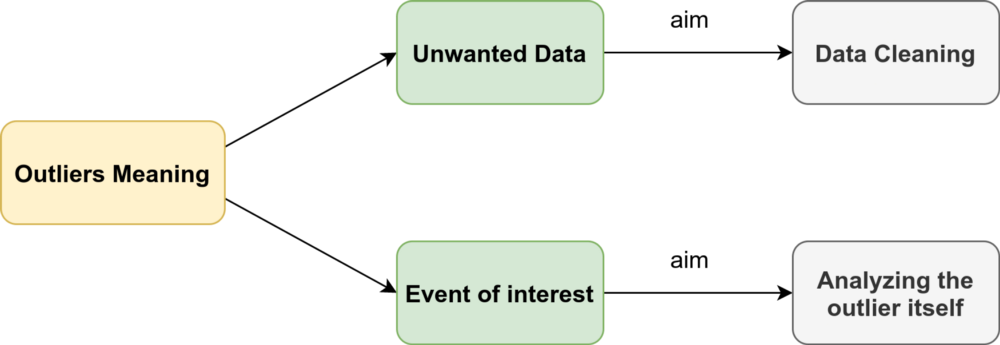
Comme le montre la figure ci-dessus, les valeurs aberrantes dans les séries chronologiques peuvent avoir deux significations différentes. La distinction sémantique entre eux repose principalement sur votre intérêt en tant qu’analyste ou sur le scénario particulier.
Ces observations ont été liées à du bruit, à des données erronées ou indésirables, qui en soi n’intéressent pas l’analyste. Dans ces cas, les valeurs aberrantes doivent être supprimées ou corrigées pour améliorer la qualité des données et générer un ensemble de données plus propre pouvant être utilisé par d’autres algorithmes d’exploration de données. Par exemple, les erreurs de transmission des capteurs sont éliminées pour obtenir des prédictions plus précises, car l’objectif principal est de faire des prédictions.
Néanmoins, ces dernières années – notamment dans le domaine des données de séries chronologiques – de nombreux chercheurs se sont efforcés de détecter et d’analyser des phénomènes inhabituels mais intéressants. La détection de la fraude est un bon exemple : l’objectif principal est de détecter et d’analyser la valeur aberrante elle-même. Ces observations sont souvent appelées anomalies.
Le problème de détection d’anomalies pour les séries chronologiques est généralement formulé comme l’identification de points de données aberrants par rapport à une norme ou à un signal habituel. Jetez un œil à quelques types de valeurs aberrantes :

Point Outlier
Une valeur aberrante ponctuelle est une donnée qui se comporte de manière inhabituelle dans une instance temporelle spécifique par rapport aux autres valeurs de la série chronologique (valeur aberrante globale) ou à ses points voisins (valeur aberrante locale).
Les valeurs aberrantes ponctuelles peuvent être univariées ou multivariées, selon qu’elles affectent respectivement une ou plusieurs variables dépendantes du temps.
La figure contient deux valeurs aberrantes ponctuelles univariées, O1 et O2, tandis que la série chronologique multivariée est composée de trois variables et présente des valeurs aberrantes ponctuelles univariées (O3) et multivariées (O1 et O2).
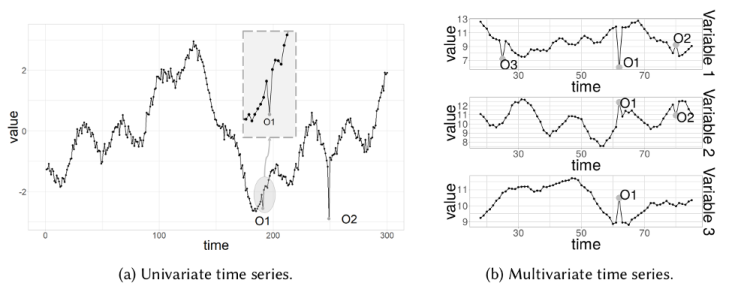
Nous examinerons plus en détail les valeurs aberrantes univariées dans la section Détection des anomalies.
Sous-séquence outlier
Cela signifie des points consécutifs dans le temps dont le comportement conjoint est inhabituel, bien que chaque observation prise individuellement ne soit pas nécessairement un point aberrant. Les valeurs aberrantes de sous-séquence peuvent également être globales ou locales et peuvent affecter une (valeur aberrante de sous-séquence univariée) ou plusieurs (valeur aberrante de sous-séquence multivariée) variables dépendantes du temps.
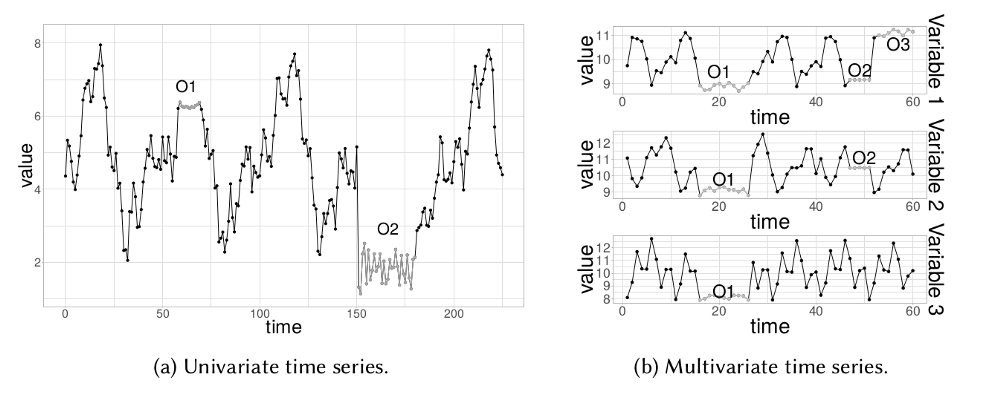
Détection par décomposition
STL signifie procédure de décomposition des tendances saisonnières basée sur LOESS. Cette technique vous donne la possibilité de diviser votre signal de série chronologique en trois parties : saisonnière, tendance et résiduelle.
Il fonctionne pour les séries chronologiques saisonnières, qui sont également le type de données de séries chronologiques le plus populaire. Pour générer un tracé de décomposition STL, nous utilisons simplement les modèles de statistiques toujours étonnants pour faire le gros du travail à notre place.
plt.rc('figure',figsize=(12,8))
plt.rc('font',size=15)
result = seasonal_decompose(lim_catfish_sales,model='additive')
fig = result.plot()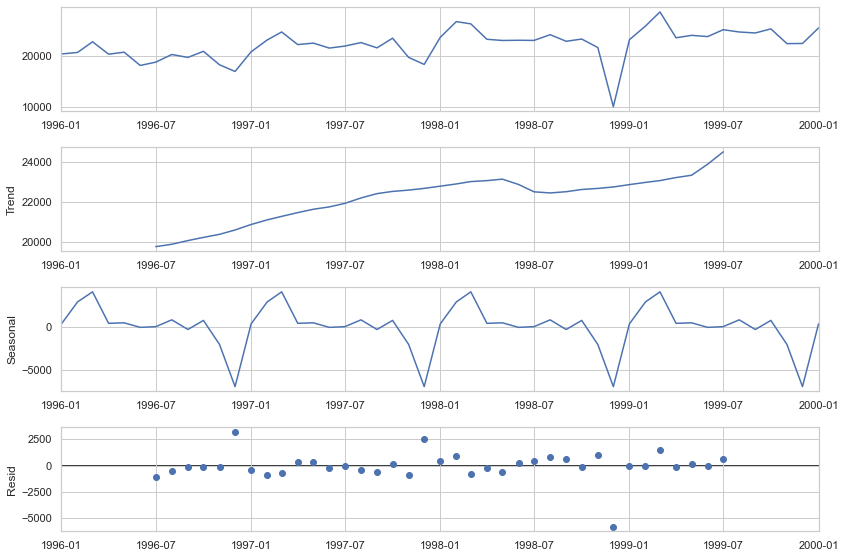
Si nous analysons l’écart des résidus et introduisons un seuil pour celui-ci, nous obtiendrons un algorithme de détection d’anomalies. Pour mettre en œuvre cela, nous n’avons besoin que des données sur les résidus de la décomposition.
plt.rc('figure',figsize=(12,6))
plt.rc('font',size=15)
fig, ax = plt.subplots()
x = result.resid.index
y = result.resid.values
ax.plot_date(x, y, color='black',linestyle='--')
ax.annotate('Anomaly', (mdates.date2num(x[35]), y[35]), xytext=(30, 20),
textcoords='offset points', color='red',arrowprops=dict(facecolor='red',arrowstyle='fancy'))
fig.autofmt_xdate()
plt.show()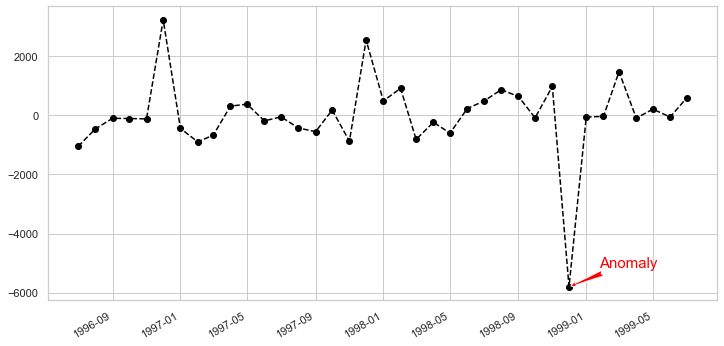
C’est simple, robuste, il peut gérer de nombreuses situations différentes et toutes les anomalies peuvent toujours être interprétées intuitivement.
Le plus gros inconvénient de cette technique réside dans les options de réglage rigides. Hormis le seuil et peut-être l’intervalle de confiance, vous ne pouvez pas faire grand-chose à ce sujet. Par exemple, vous suivez les utilisateurs de votre site Web qui a été fermé au public puis a été soudainement ouvert. Dans ce cas, vous devez suivre séparément les anomalies qui se produisent avant et après les périodes de lancement.
Détection par arbres de régression
Nous pouvons utiliser la puissance et la robustesse des arbres de décision pour identifier les valeurs aberrantes/anomalies dans les données de séries chronologiques.
L’idée principale, qui diffère des autres méthodes populaires de détection des valeurs aberrantes, est qu’Isolement Forest identifie explicitement les anomalies au lieu de profiler les points de données normaux. Isolation Forest, comme toute méthode d’ensemble d’arbres, est basée sur des arbres de décision.
En d’autres termes, Isolation Forest détecte les anomalies uniquement sur la base du fait que les anomalies sont des points de données peu nombreux et différents. L’isolement des anomalies est mis en œuvre sans recourir à aucune mesure de distance ou de densité.
Lors de l’application d’un modèle IsolationForest, nous définissons contamination = outliers_fraction, ce qui indique au modèle quelle proportion de valeurs aberrantes est présente dans les données. Il s’agit d’une métrique d’essai/erreur. Ajuster et prédire (données) effectue une détection des valeurs aberrantes sur les données et renvoie 1 pour la normale, -1 pour l’anomalie. Enfin, nous visualisons les anomalies avec la vue Time Series.
Faisons-le étape par étape. Tout d’abord, visualisez les données de la série chronologique :
plt.rc('figure',figsize=(12,6))
plt.rc('font',size=15)
catfish_sales.plot()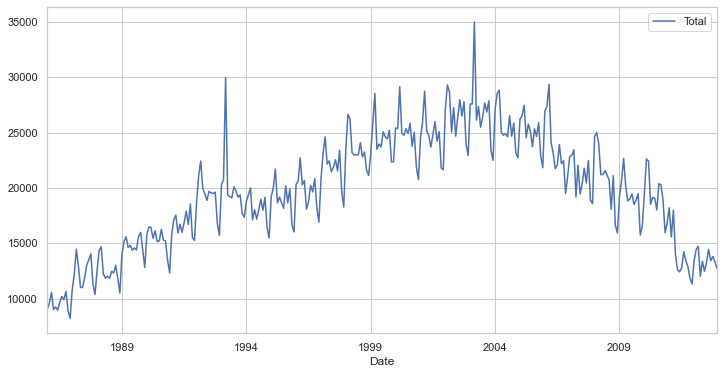
Ensuite, nous devons définir certains paramètres comme la fraction aberrante et entraîner notre modèle IsolationForest. Nous pouvons utiliser le scikit-learn très utile pour implémenter l’algorithme Isolation Forest (voir git au début de la page).
outliers_fraction = float(.01)
scaler = StandardScaler()
np_scaled = scaler.fit_transform(catfish_sales.values.reshape(-1, 1))
data = pd.DataFrame(np_scaled)
# train isolation forest
model = IsolationForest(contamination=outliers_fraction)
model.fit(data)catfish_sales['anomaly'] = model.predict(data)
# visualization
fig, ax = plt.subplots(figsize=(10,6))
a = catfish_sales.loc[catfish_sales['anomaly'] == -1, ['Total']] #anomaly
ax.plot(catfish_sales.index, catfish_sales['Total'], color='black', label = 'Normal')
ax.scatter(a.index,a['Total'], color='red', label = 'Anomaly')
plt.legend()
plt.show();
Comme vous pouvez le constater, l’algorithme a fait un très bon travail en identifiant nos anomalies implantées, mais il a également qualifié au début quelques points de « valeurs aberrantes ». Cela est dû à deux raisons :
- Au départ, l’algorithme est assez naïf pour pouvoir comprendre ce qui constitue une anomalie. Plus il obtient de données, plus il est capable de voir de variance et il s’ajuste lui-même.
- Si vous voyez beaucoup de vrais négatifs, cela signifie que votre paramètre de contamination est trop élevé. À l’inverse, si vous ne voyez pas les points rouges là où ils devraient être, le paramètre de contamination est réglé trop bas.
Le plus grand avantage de cette technique est que vous pouvez introduire autant de variables ou de fonctionnalités aléatoires que vous le souhaitez pour créer des modèles plus sophistiqués.
La faiblesse est qu’un nombre croissant de fonctionnalités peuvent commencer à avoir un impact assez rapidement sur vos performances de calcul. Dans ce cas, vous devez sélectionner les fonctionnalités avec soin.
Détection par prédiction
La détection d’anomalies à l’aide de la prévision est basée sur une approche selon laquelle plusieurs points du passé génèrent une prévision du point suivant avec l’ajout d’une variable aléatoire, qui est généralement du bruit blanc.
Comme vous pouvez l’imaginer, les points prévus dans le futur généreront de nouveaux points et ainsi de suite. Son effet évident sur l’horizon de prévision est que le signal devient plus fluide.
La partie difficile de l’utilisation de cette méthode est que vous devez sélectionner le nombre de différences, le nombre d’autorégressions et les coefficients d’erreur de prévision. Chaque fois que vous travaillez avec un nouveau signal, vous devez créer un nouveau modèle de prévision.
Un autre obstacle est que votre signal doit rester stationnaire après la différenciation. En termes simples, cela signifie que votre signal ne doit pas dépendre du temps, ce qui constitue une contrainte importante.
Nous pouvons utiliser différentes méthodes de prévision telles que les moyennes mobiles, l’approche autorégressive et ARIMA avec ses différentes variantes. La procédure de détection des anomalies avec ARIMA est la suivante :
- Prédisez le nouveau point à partir des données passées et trouvez la différence d’ampleur avec celles des données d’entraînement.
- Choisissez un seuil et identifiez les anomalies en fonction de ce seuil de différence.
Pour tester cette technique, nous allons utiliser un module populaire dans les séries chronologiques appelé fbprophet. Ce module s’adresse spécifiquement à la stationnarité et à la saisonnalité, et peut être réglé avec certains hyper-paramètres.
from fbprophet import Prophetdef fit_predict_model(dataframe, interval_width = 0.99, changepoint_range = 0.8):
m = Prophet(daily_seasonality = False, yearly_seasonality = False, weekly_seasonality = False,
seasonality_mode = 'additive',
interval_width = interval_width,
changepoint_range = changepoint_range)
m = m.fit(dataframe)
forecast = m.predict(dataframe)
forecast['fact'] = dataframe['y'].reset_index(drop = True)
return forecast
pred = fit_predict_model(t)Définissons maintenant la fonction de prévision. Une chose importante à noter ici est que fbprophet ajoutera des métriques supplémentaires en tant que fonctionnalités, afin de mieux identifier les anomalies. Par exemple, la variable de série chronologique prévue (par le modèle), les limites supérieure et inférieure de la variable de série chronologique cible et la mesure de tendance.
Nous devons maintenant pousser la variable pred vers une autre fonction, qui détectera les anomalies en fonction d’un seuil de limite inférieure et supérieure dans la variable de série temporelle.
def detect_anomalies(forecast):
forecasted = forecast[['ds','trend', 'yhat', 'yhat_lower', 'yhat_upper', 'fact']].copy()
forecasted['anomaly'] = 0
forecasted.loc[forecasted['fact'] > forecasted['yhat_upper'], 'anomaly'] = 1
forecasted.loc[forecasted['fact'] < forecasted['yhat_lower'], 'anomaly'] = -1
#anomaly importances
forecasted['importance'] = 0
forecasted.loc[forecasted['anomaly'] ==1, 'importance'] =
(forecasted['fact'] - forecasted['yhat_upper'])/forecast['fact']
forecasted.loc[forecasted['anomaly'] ==-1, 'importance'] =
(forecasted['yhat_lower'] - forecasted['fact'])/forecast['fact']
return forecasted
pred = detect_anomalies(pred)
Cet algorithme gère bien différents paramètres de saisonnalité, tels que mensuels ou annuels, et prend en charge nativement toutes les métriques de séries chronologiques.
Étant donné que cette technique est basée sur la prévision, elle aura des difficultés dans des scénarios de données limitées. La qualité de la prédiction dans des données limitées sera moindre, tout comme la précision de la détection des anomalies.
Détection par clustering
L’approche est assez simple. Les instances de données qui ne font pas partie des clusters définis peuvent potentiellement être marquées comme anomalies.
Par souci de visualisation, nous utiliserons un ensemble de données différent qui correspond à une série temporelle multivariée avec une ou plusieurs variables temporelles. L’ensemble de données sera un sous-ensemble de celui trouvé ici (les colonnes/caractéristiques sont les mêmes).
Description de l’ensemble de données : Les données contiennent des informations sur les achats et les achats ainsi que des informations sur la compétitivité des prix.
Maintenant, pour traiter les k-moyennes, nous devons d’abord connaître le nombre de clusters que nous allons traiter. La méthode Elbow fonctionne assez efficacement pour cela.
La méthode Elbow est un graphique du nombre de clusters par rapport à la variance expliquée/objectif/score
Pour implémenter cela, nous utiliserons l’implémentation de K-means par scikit-learn.
data = df[['price_usd', 'srch_booking_window', 'srch_saturday_night_bool']]
n_cluster = range(1, 20)
kmeans = [KMeans(n_clusters=i).fit(data) for i in n_cluster]
scores = [kmeans[i].score(data) for i in range(len(kmeans))]
fig, ax = plt.subplots(figsize=(10,6))
ax.plot(n_cluster, scores)
plt.xlabel('Number of Clusters')
plt.ylabel('Score')
plt.title('Elbow Curve')
plt.show();
À partir de la courbe coudée ci-dessus, nous voyons que le graphique se stabilise après 10 clusters, ce qui implique que l’ajout de clusters supplémentaires n’explique pas beaucoup plus la variance de notre variable pertinente ; dans ce cas, price_usd.
Nous définissons n_clusters = 10 et, lors de la génération de la sortie k-means, utilisons les données pour tracer les clusters 3D.
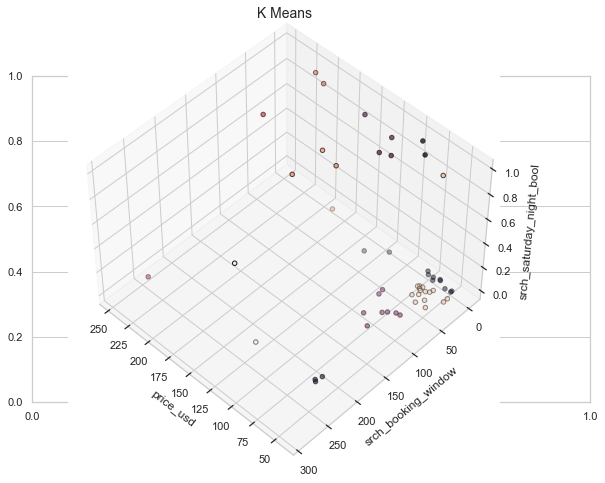
Il nous faut maintenant connaître le nombre de composants (fonctionnalités) à conserver.
data = df[['price_usd', 'srch_booking_window', 'srch_saturday_night_bool']]
X = data.values
X_std = StandardScaler().fit_transform(X)
#Calculating Eigenvecors and eigenvalues of Covariance matrix
mean_vec = np.mean(X_std, axis=0)
cov_mat = np.cov(X_std.T)
eig_vals, eig_vecs = np.linalg.eig(cov_mat)
# Create a list of (eigenvalue, eigenvector) tuples
eig_pairs = [ (np.abs(eig_vals[i]),eig_vecs[:,i]) for i in range(len(eig_vals))]
eig_pairs.sort(key = lambda x: x[0], reverse= True)
# Calculation of Explained Variance from the eigenvalues
tot = sum(eig_vals)
var_exp = [(i/tot)*100 for i in sorted(eig_vals, reverse=True)] # Individual explained variance
cum_var_exp = np.cumsum(var_exp) # Cumulative explained variance
plt.figure(figsize=(10, 5))
plt.bar(range(len(var_exp)), var_exp, alpha=0.3, align='center', label='individual explained variance', color = 'y')
plt.step(range(len(cum_var_exp)), cum_var_exp, where='mid',label='cumulative explained variance')
plt.ylabel('Explained variance ratio')
plt.xlabel('Principal components')
plt.legend(loc='best')
plt.show();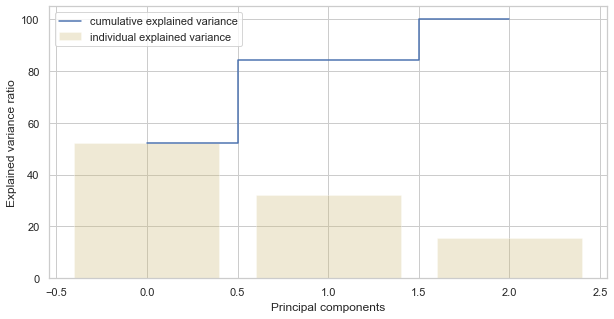
On voit que la première composante explique près de 50 % de la variance. La deuxième composante explique plus de 30 %. Cependant, notez que presque aucun des composants n’est vraiment négligeable. Les 2 premiers composants contiennent plus de 80 % des informations. Nous définirons donc n_components=2.
L’hypothèse sous-jacente à la détection des anomalies basée sur le clustering est que si nous regroupons les données, les données normales appartiendront à des clusters tandis que les anomalies n’appartiendront à aucun cluster ou appartiendront à de petits clusters.
Nous utilisons les étapes suivantes pour rechercher et visualiser les anomalies :
- Calculez la distance entre chaque point et son centre de gravité le plus proche. Les plus grandes distances sont considérées comme des anomalies.
- Nous utilisons outliers_fraction pour fournir des informations à l’algorithme sur la proportion de valeurs aberrantes présentes dans notre ensemble de données, de la même manière que l’algorithme IsolationForest. Il s’agit en grande partie d’un hyperparamètre qui nécessite un hit/essai ou une recherche sur grille pour être correctement défini – comme chiffre de départ, estimons, outliers_fraction=0,1
- Calculez number_of_outliers à l’aide de outliers_fraction.
- Définissez le seuil comme distance minimale de ces valeurs aberrantes.
- Le résultat de l’anomalie d’anomalie1 contient la méthode ci-dessus Cluster (0 : normal, 1 : anomalie).
- Visualisez les anomalies avec la vue cluster.
- Visualisez les anomalies avec la vue Time Series.
# return Series of distance between each point and its distance with the closest centroid
def getDistanceByPoint(data, model):
distance = pd.Series()
for i in range(0,len(data)):
Xa = np.array(data.loc[i])
Xb = model.cluster_centers_[model.labels_[i]-1]
distance.at[i]=np.linalg.norm(Xa-Xb)
return distance
outliers_fraction = 0.1
# get the distance between each point and its nearest centroid. The biggest distances are considered as anomaly
distance = getDistanceByPoint(data, kmeans[9])
number_of_outliers = int(outliers_fraction*len(distance))
threshold = distance.nlargest(number_of_outliers).min()
# anomaly1 contain the anomaly result of the above method Cluster (0:normal, 1:anomaly)
df['anomaly1'] = (distance >= threshold).astype(int)
fig, ax = plt.subplots(figsize=(10,6))
colors = {0:'blue', 1:'red'}
ax.scatter(df['principal_feature1'], df['principal_feature2'], c=df["anomaly1"].apply(lambda x: colors[x]))
plt.xlabel('principal feature1')
plt.ylabel('principal feature2')
plt.show();
Désormais, afin de voir les anomalies par rapport aux fonctionnalités du monde réel, nous traitons la trame de données que nous avons créée à l’étape précédente.
df = df.sort_values('date_time')
fig, ax = plt.subplots(figsize=(10,6))
a = df.loc[df['anomaly1'] == 1, ['date_time', 'price_usd']] #anomaly
ax.plot(pd.to_datetime(df['date_time']), df['price_usd'], color='k',label='Normal')
ax.scatter(pd.to_datetime(a['date_time']),a['price_usd'], color='red', label='Anomaly')
ax.xaxis_date()
plt.xlabel('Date Time')
plt.ylabel('price in USD')
plt.legend()
fig.autofmt_xdate()
plt.show()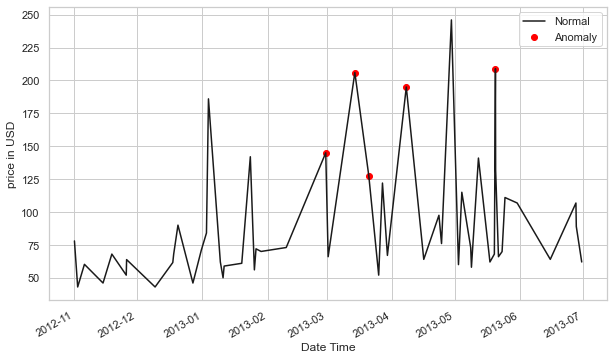
Cette méthode est capable d’encapsuler assez bien les pics, avec quelques ratés bien sûr. Une partie du problème peut être due au fait que outlier_fraction n’a pas joué avec de nombreuses valeurs.
Le plus grand avantage de cette technique est similaire à d’autres techniques non supervisées, à savoir que vous pouvez introduire autant de variables ou de fonctionnalités aléatoires que vous le souhaitez pour créer des modèles plus sophistiqués.
La faiblesse est qu’un nombre croissant de fonctionnalités peuvent commencer à avoir un impact assez rapidement sur vos performances de calcul. En plus de cela, il y a davantage d’hyper-paramètres à régler et à corriger, il y a donc toujours un risque de variation élevée des performances du modèle.
Détection par autoencodeur
Les auto-encodeurs sont une technique non supervisée qui recrée les données d’entrée tout en extrayant leurs caractéristiques à travers différentes dimensions. Donc, en d’autres termes, si l’on utilise la représentation latente des données des auto-encodeurs, cela correspond à une réduction de dimensionnalité. De nombreuses techniques basées sur la distance (par exemple les KNN) souffrent de la malédiction de la dimensionnalité lorsqu’elles calculent les distances de chaque point de données dans l’espace complet des fonctionnalités. La haute dimensionnalité doit être réduite.
Il existe de nombreux outils utiles, tels que l’analyse en composantes principales (ACP), pour détecter les valeurs aberrantes. Pourquoi avons-nous besoin d’auto-encodeurs ? La raison en est que l’ACP utilise l’algèbre linéaire pour transformer. En revanche, les techniques d’auto-encodeur peuvent effectuer des transformations non linéaires grâce à leur fonction d’activation non linéaire et leurs multiples couches.
Il est plus efficace d’entraîner plusieurs couches avec un encodeur automatique, plutôt que d’entraîner une énorme transformation avec PCA. Les techniques d’auto-encodeur montrent ainsi leurs mérites lorsque les problèmes de données sont de nature complexe et non linéaire.
Nous pouvons implémenter des auto-encodeurs avec des frameworks populaires comme TensorFlow ou Pytorch, mais – par souci de simplicité – nous allons utiliser un module python appelé PyOD, qui construit des auto-encodeurs en interne en utilisant quelques entrées de l’utilisateur.
Pour la partie données, utilisons la fonction utilitaire generate_data() de PyOD pour générer 25 variables, 500 observations et dix pour cent de valeurs aberrantes.
import numpy as np
import pandas as pd
from pyod.models.auto_encoder import AutoEncoder
from pyod.utils.data import generate_data
contamination = 0.1 # percentage of outliers
n_train = 500 # number of training points
n_test = 500 # number of testing points
n_features = 25 # Number of features
X_train, y_train, X_test, y_test = generate_data(
n_train=n_train, n_test=n_test,
n_features= n_features,
contamination=contamination,random_state=1234)
X_train = pd.DataFrame(X_train)
X_test = pd.DataFrame(X_test)from sklearn.preprocessing import StandardScaler
X_train = StandardScaler().fit_transform(X_train)
X_train = pd.DataFrame(X_train)
X_test = StandardScaler().fit_transform(X_test)
X_test = pd.DataFrame(X_test)from sklearn.decomposition import PCA
pca = PCA(2)
x_pca = pca.fit_transform(X_train)
x_pca = pd.DataFrame(x_pca)
x_pca.columns=['PC1','PC2']
cdict = {0: 'red', 1: 'blue'}
# Plot
import matplotlib.pyplot as plt
plt.scatter(X_train[0], X_train[1], c=y_train, alpha=1)
plt.title('Scatter plot')
plt.xlabel('x')
plt.ylabel('y')
plt.show()
Maintenant tunons un autoencodeur. [25, 2, 2, 25]. La couche d’entrée et la couche de sortie comportent chacune 25 neurones. Il y a deux couches cachées, chacune comportant deux neurones.
clf = AutoEncoder(hidden_neurons =[25, 2, 2, 25])
clf.fit(X_train)Appliquons le modèle entraîné Clf pour prédire le score d’anomalie pour chaque observation dans les données de test. Comment définit-on une valeur aberrante ? Une valeur aberrante est un point éloigné des autres points, le score aberrant est donc défini par la distance. La fonction PyOD .decision_function() calcule la distance, ou le score d’anomalie, pour chaque point de données.
# Get the outlier scores for the train data
y_train_scores = clf.decision_scores_
# Predict the anomaly scores
y_test_scores = clf.decision_function(X_test) # outlier scores
y_test_scores = pd.Series(y_test_scores)
# Plot it!
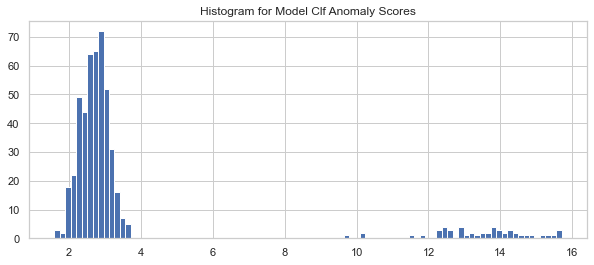
import matplotlib.pyplot as plt
plt.hist(y_test_scores, bins='auto')
plt.title("Histogram for Model Clf1 Anomaly Scores")
plt.show()Si nous utilisons un histogramme pour compter la fréquence par le score d’anomalie, nous verrons que les scores élevés correspondent à une fréquence faible — preuve de valeurs aberrantes. Nous choisissons 4,0 comme point de coupure et ceux >=4,0 comme valeurs aberrantes.
Attribuons les observations avec des scores d’anomalie inférieurs à 4,0 au cluster 0 et au cluster 1 pour celles supérieures à 4,0. Calculons également les statistiques récapitulatives par cluster en utilisant .groupby() . Ce modèle a identifié 50 valeurs aberrantes (non présentées).
df_test = X_test.copy()
df_test['score'] = y_test_scores
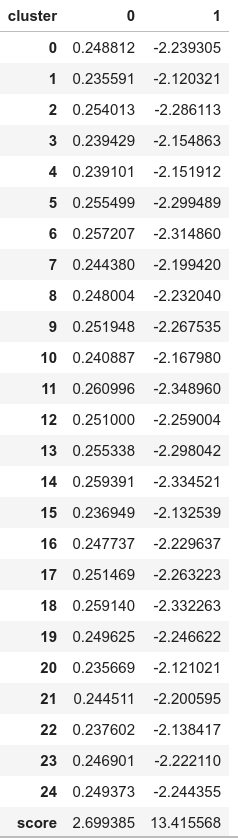
df_test['cluster'] = np.where(df_test['score']<4, 0, 1)
df_test['cluster'].value_counts()
df_test.groupby('cluster').mean()Le résultat suivant montre les valeurs moyennes des variables dans chaque cluster. Les valeurs du cluster « 1 » (le cluster anormal) sont très différentes de celles du cluster « 0 » (le cluster normal). Les valeurs du « score » montrent la distance moyenne de ces observations par rapport aux autres. Un « score » élevé signifie que l’observation est très éloignée de la norme.
De cette façon, nous pouvons distinguer et étiqueter assez parfaitement les données typiques et les anomalies.
Les encodeurs automatiques peuvent gérer facilement des données de grande dimension. En ce qui concerne son comportement de non-linéarité, il peut trouver des modèles complexes dans des ensembles de données de grande dimension.
Puisqu’il s’agit d’une stratégie basée sur l’apprentissage en profondeur, elle sera particulièrement difficile si les données sont moindres. Les coûts de calcul monteront en flèche si la profondeur du réseau augmente et en traitant du Big Data.
Gérer les anomalies avec du lissage
Les méthodes statistiques vous permettent d’ajuster la valeur de votre valeur aberrante pour qu’elle corresponde à la distribution d’origine. Voyons une des méthodes utilisées pour lisser les anomalies.
L’idée est d’atténuer l’anomalie en utilisant les données du DateTime précédent. Par exemple, pour compenser une consommation soudaine d’électricité due à un événement survenu dans votre maison, vous pouvez prendre la moyenne des consommations au cours du même mois pour les années précédentes.
Mettons en œuvre la même chose pour avoir une image claire. Nous utiliserons les mêmes données sur les ventes de poisson-chat que nous avons utilisées plus tôt. Nous pouvons ajuster avec la moyenne en utilisant le script ci-dessous.
adjusted_data = lim_catfish_sales.copy()
adjusted_data.loc[curr_anomaly] = december_data[(december_data.index != curr_anomaly) & (december_data.index < test_data.index[0])].mean()plt.figure(figsize=(10,4))
plt.plot(lim_catfish_sales, color='firebrick', alpha=0.4)
plt.plot(adjusted_data)
plt.title('Catfish Sales in 1000s of Pounds', fontsize=20)
plt.ylabel('Sales', fontsize=16)
for year in range(start_date.year,end_date.year):
plt.axvline(pd.to_datetime(str(year)+'-01-01'), color='k', linestyle='--', alpha=0.2)
plt.axvline(curr_anomaly, color='k', alpha=0.7)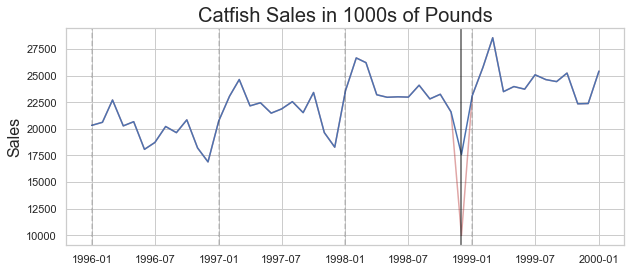
De cette façon, vous pouvez procéder à l’application de prévisions ou d’analyses sans trop vous soucier de l’asymétrie de vos résultats.
Il existe de nombreuses méthodes pour traiter des données non chronologiques, mais elles ne peuvent malheureusement pas être utilisées directement dans Timeseries en raison de la différence dans les structures sous-jacentes. Les méthodes de traitement sans séries chronologiques impliquent de nombreuses méthodes basées sur la distribution qui ne peuvent pas être simplement traduites en données Timeseries.
Effacer les anomalies
La dernière option si aucune des deux solutions ci-dessus ne suscite de débat dans votre solution est de supprimer les anomalies. Ceci n’est pas recommandé (car vous vous débarrassez essentiellement de certaines informations potentiellement précieuses) à moins que cela ne soit absolument nécessaire et que cela ne nuise pas à l’analyse future.
Vous pouvez utiliser la fonctionnalité .drop() dans les pandas après identification. Il fera le gros du travail à votre place.
