Le test de Pesaran-Timmermann détermine si une prévision permet de prédire correctement le changement de direction d’une série chronologique. C’est à dire sa précision directionnelle.
Description
Pour toute série temporelle ti comportant n éléments, nous définissons d’abord
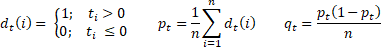
Supposons maintenant que nous ayons une série chronologique yi avec n éléments qui est prévue par zi et définissons
Sous l’hypothèse nulle selon laquelle z ne prévoit pas la direction du changement de y (c’est-à-dire le signe de yi), nous avons la statistique de test suivante
Le test de Pesaran-Timmermann est un test unilatéral dans lequel la région critique (où l’hypothèse nulle est rejetée) est la queue supérieure de la distribution normale standard. Ainsi si
1 – NORM.S.DIST(PT, VRAI) < α
nous pouvons alors rejeter l’hypothèse nulle et affirmer avec une confiance de 1 – α que la prévision prédit avec précision le signe de yi.
Notez que si le signe de tous les éléments de yi (ou zi) est le même, alors la statistique PT ne sera pas définie.
Exemple
Utilisez le test de Pesaran-Timmermann pour déterminer si les prévisions de la colonne B de la figure prévoient avec précision la direction du changement pour les données de la colonne A.
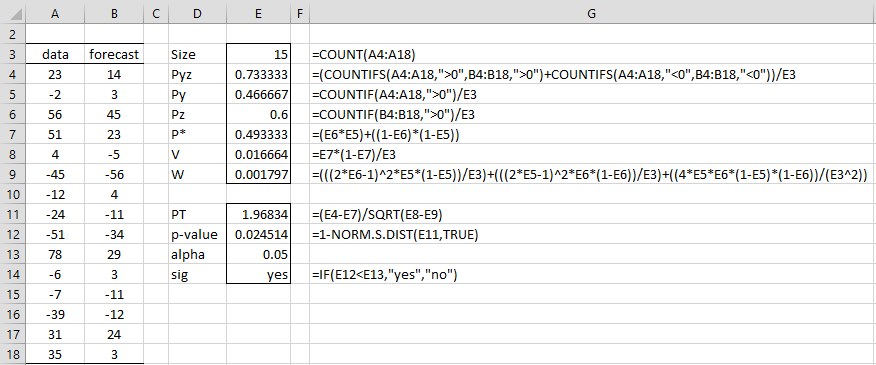
Le test prouve que la prévision prévoit avec précision la direction du changement dans les données.
FR 
EN 
ES