Contenus
ToggleExercices corrigés de programmation linéaire (forme primale)
Ce TD propose divers exercices corrigés sur la modélisation en forme primale de programmation linéaire.

Tutoriel
Un fabriquant d’outillage de fraisage fabrique deux types de fraises : A et B. Les fraises de type A se vendent 300 l’unité, et se fabrique à avec 1 unité d’acier, 2 unités de carbure amovible et 1 unité de diamant synthétique. Les fraises de type B se vendent 200 l’unité, et se fabrique à avec 2 unité d’acier, 1 unités de carbure amovible et 1 unité de diamant synthétique.
Les stocks sont de 5 unités d’acier, 5 unités de carbure et 2 unités de diamant. Le fabriquant souhaite construire au moins 5 fraises de type A et 5 fraises de type B. Le coût d’entretien de l’usine est de 2500. Comment le fabriquant doit-il répartir sa production pour maximiser son profit, est-ce rentable ?
Dans un premier temps il faut réaliser le programme linéaire :
- Fonction objectif : z = 300A+200B-2500
- Contraintes :
- A+2B ≤ 5
- 2A+B ≤ 5
- A+B ≤ 2
- A ≥ 5
- B ≥ 5
Le programme n’est pas sous forme canonique, il faut le rendre sous cette forme avant de le résoudre.
Posons x1 = A-5 et x2 = B-5. Le programme linéaire devient le suivant :
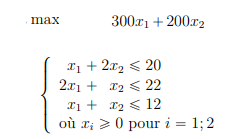
Le programme linéaire possède 2 variables, il est donc possible de le résoudre graphiquement. Les contraintes donnent le domaine des solutions suivant :
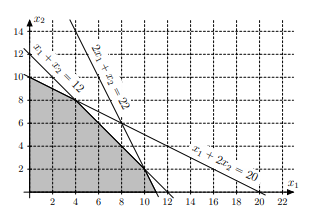
Le gradient de la fonction objectif est (3,2), ce qui donne pour point extrême l’intersection de la deuxième et troisième contrainte. Il faut donc résoudre le système :

Qui a pour solution le vecteur (10, 2). Ce qui donne dans le problème initial le vecteur (15, 7) et pour fonction objectif égale à 900. L’opération est positif donc profitable pour l’usine.
Exercice 1
Un brooker a besoin, pour sa clientèle, de 108 MWh d’électricité pour la ville 1 et de 96 MWh d’électricité pour la ville 2. Cependant, les lois de Kirchhoff ne permettent pas à un distributeur de cibler une ville unique pour le transit énergétique. Deux distributeurs desservent ces villes : le Distributeur A peut envoyer 12 MWh à la ville 1 et 8MWh à la ville 2 par lot acheté; le Distributeur B peut envoyer 9 MWh à la ville 1 et 12 MWh à la ville 2 par lot acheté. Les lots ont tous le même prix. Combien de lots doit acheter le brooker pour combler la demande énergétique des deux villes ? Résoudre par méthode graphique.
Le programme linéaire est le suivant : X1 pour le premier lot et X2 pour le deuxième lot
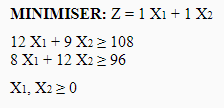
Ce qui donne pour résolution graphique :
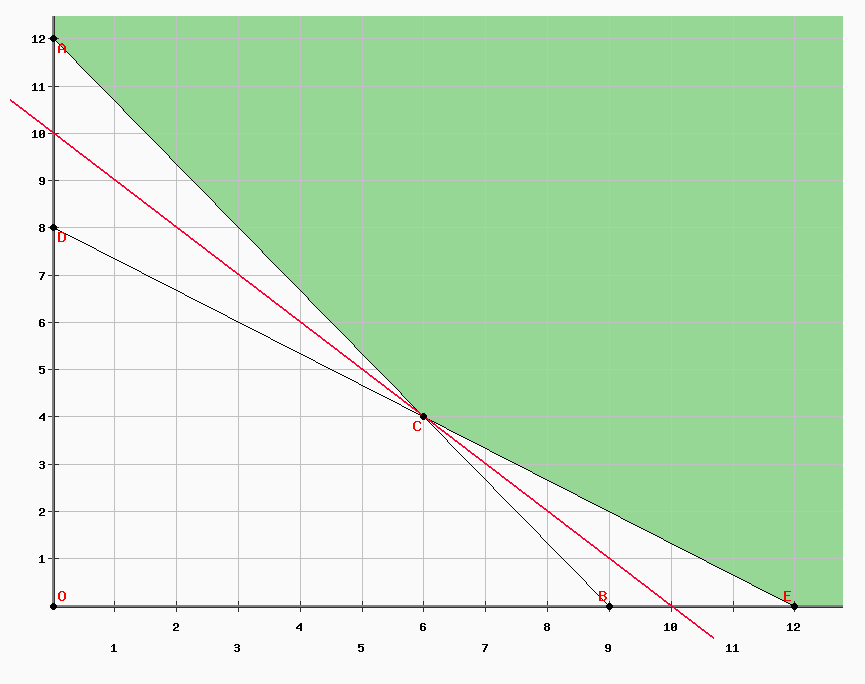
Le gradient est (-1, -1) car c’est un minimum (min f(x) = – max -f(x)). Dans le domaine de définition en vert, le point C est le seul extremum étant un optimum global. La résolution du système précédent sous forme d’égalité donne pour coordonnées (6, 4) avec Z = 10.
Exercice 2
Résoudre par la méthode graphique puis par le simplexe les problèmes suivants :
- Une compagnie fabriquant deux types de produits cherchent à maximiser son profit. Voici sa feuille de route.
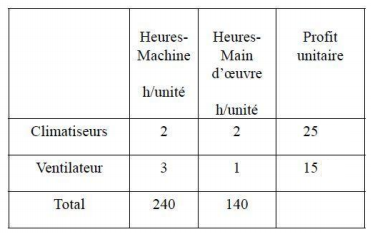
- De même avec le programme linéaire suivant :

La méthodologie est toujours identique pour la partie résolution graphique. Voici les corrections des simplexes avec l’état initial et l’état final du tableau pour le premier exemple.
Problème 0 :

Et pour solution :

La fonction objectif a pour valeur Z = 1875 avec P1 et P2 en base (donc non nul) ayant respectivement pour valeur (25,15) comme stipuler dans la colonne b représenté par P0.
Le deuxième programme linéaire a pour solution Z = 8.2 avec le vecteur des variables de base (3.2, 1.8).
Exercice 3
Le BIM optimise la construction, la rénovation et la maintenance de bâtiments. Parmi les éléments à optimiser il y a les ouvriers. En général, il existe 4 types d’ouvriers en fonction de leur week-end. Le salaire des ouvriers dépendent de ces journées de congés :

Les demandes quotidiennes en ouvriers sont les suivantes :

Combien de personnes de chaque catégorie doit-on faire travailler de façon à satisfaire la demande et à minimiser le coût du personnel ? Donner la forme canonique du problème et résoudre à l’aide du Solver Excel.
Le programme linéaire est le suivant :
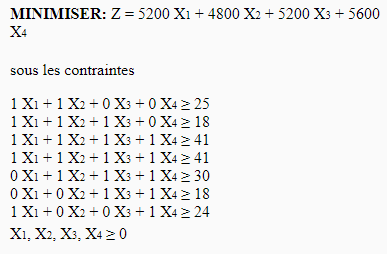
La résolution par excel est la suivante :

Le résultat est le suivant :

Notons que la solution optimale n’est pas unique. La solution donne des nombres entiers, ce qui est pratique compte tenu du problème (il parait évident qu’il faut des individus « entier »).
Exercice 4
Une entreprise fabrique trois types de produits, A, B et C. Chaque produit nécessite des matières premières et de la main d’oeuvre, ainsi que de l’espace de stockage. Voici les besoins en matières premières, mains d’oeuvre et stockage pour une unité de chacun des 3 types de produits :
- Produit A : 4 kg de matières premières, 2 heures de main d’oeuvre, 1 unité de volume.
- Produit B : 2 kg de matières premières, 1/2 heure de main d’oeuvre 1 unité de volume.
- Produit C : 1 kg de matières premières, 3 heures de main d’oeuvre, 1 unité de volume.
Chaque produit rapporte 6 euros s’il est de type A, 2 euros s’il est de type B, et 4 euros s’il est de type C. Les ressources disponibles sont 6000 kg de matières premières, 4000 heures de main d’oeuvre, et 2500 unités de volume de stockage.
Modélisation le programme linéaire et le résoudre à la main à l’aide du simplexe.
Un concurrent, qui manque de matières premières, propose d’en racheter 300 kg à cette entreprise, au prix de 1.5 euros par kg. Pensez-vous que l’entreprise devrait accepter cette proposition ? (On supposera qu’elle l’accepte si elle est rentable, résoudre le problème à la main avec le simplexe.)
Le problème sous forme standard est le suivant :

Avec pour solution du simplexe :

Le problème du rachat a en plus dans la fonction objectif 450. La première variable a pour élément b = 5700. Dans ce cas la solution optimale est (1310, 0, 460) avec Z = 10150, donc la proposition est rentable.
Exercice 5
Une entreprise fabrique trois types de piles : sèches de type 1 (PS1), sèches de type 2 (PS2) et à combustible (PC). Le processus de fabrication comporte trois étapes : l’assemblage, un test de qualité, un traitement d’isolation. Seules les piles satisfaisant le test de qualité sont soumises au traitement d’isolation. Les piles qui ratent le test de qualité sont mises au rebut. Au cours du mois prochain, l’entreprise disposera en temps-machine de 9000 heures pour l’assemblage, de 1200 heures pour les tests de qualité et de 8500 heures pour le traitement d’isolation. Le tableau suivant résume les informations pertinentes du procédé de fabrication :

Quel est le nombre optimal de piles de chaque type à fabriquer le mois prochain si l’entreprise est assurée de vendre toute sa production ?
Posons X1, X2, X3 les trois variables représentant le nombre de piles valides de chaque types et X4, X5, X6 les trois variables représentant le nombre de piles non valides de chaque types.
Le programme linéaire sous forme canonique est le suivant :
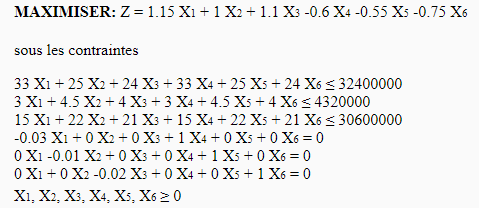
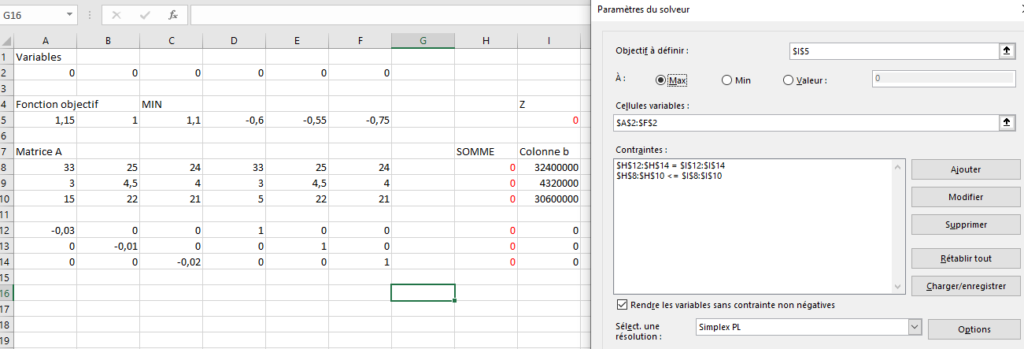
Ce qui donne comme solution (419417.476, 0, 741176.471) pour les piles valides et pour fonction objectif Z=1278957,05. La solution ne donnant pas de résultat en nombre entier, il est possible de tronquer la partie flottante (attention, ce ne sera plus une solution optimale !).
Exercice 6
Dans un réseau électrique, la quantité d’énergie pouvant transiter des centrales vers les villes est limité par les capacités des lignes à très hautes tension. Le problème est décrit de la façon suivante :
- Des sources, représenté par des sommets, produisent une quantité d’énergie
- Des puits, représenté par des sommets, reçoivent une quantité d’énergie
- Des lignes, représenté par des arêtes entre une pair de sommet, par lesquels passent l’énergie.

Ce graphe se lit ainsi :
- S est une source fictive, qui décrit la production des sources énergétiques représentées par le sommet 1 et le sommet 2.
- T est un puits fictif, qui décrit la réception énergétique des villes représentées par le sommet 3 et le sommet 4.
- Les lignes sont orientés, c’est à dire que l’énergie ne passe que dans un seul sens. Par exemple la lien (1, 3) peut faire circuler jusqu’à 4 unités d’énergie entre le sommet 1 et le sommet 3.
- Les liens entre S et les sources décrient la production énergétique de la source. Par exemple le lien (S, 1) dit que la source 1 peut produire jusqu’à 10 unités d’énergie.
- Les liens entre les puits et T décrient la demande énergétique du puits. Par exemple le lien (3, T) dit que la ville 3 réclament 10 unités en énergie.
La fonction objectif de se type de problème est :
- maximiser la quantité d’énergie que l’on peut faire transiter de S à T. La solution fournira la quantité d’énergie transitant dans chaque ligne. Pour calculer ce flot, un arc est ajouté entre le puits fictif et la source fictive sans contrainte. La solution optimale est égale au flot transitant par cet arc.
Ce problème est soumis à deux types de contraintes :
- la somme des énergies entrant dans un sommet moins la somme des énergies sortant du même sommet est nulle. C’est à dire qu’il n’y a pas de pertes énergétiques dans le réseau
- l’énergie transitant par une ligne ne peut pas être supérieur à la capacité de la ligne.
- l’énergie transitant par une ligne est positive ou nulle.
Les variables sont donc :
- pour chaque ligne, une variable décrit la quantité d’énergie transitant dessus.
Formuler le problème linéaire pour le graphe donné ci-dessus et résolvez le via Excel.
Le problème linéaire s’écrit dans Excel de la façon suivant :

Ce qui donne comme résultat :

